智能系统设计-Part2.3-图像增强和滤波
灰度变换-像素处理
像素处理是最简单、理解最直观的。是对每个像素点的值直接进行变换。像素处理可以只对图像的一部分执行。
在像素处理中,变换函数被记为T,某个像素点变换前的值为r,后的值为S,$S=T(r)$。
熟悉PS的小伙伴会知道PS里面有个曲线,这个曲线其实就是变换函数的函数图像。当曲线是下图这样时,会增强对比度。
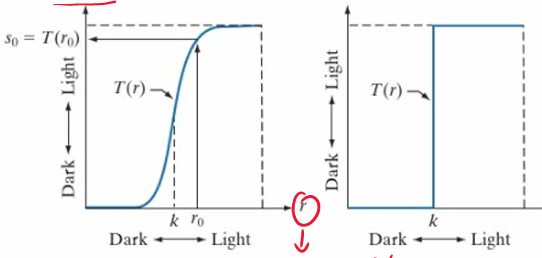
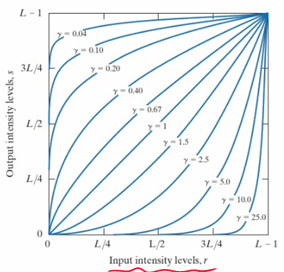
如果拖着曲线的中点朝左上或者右下移动(变成指数函数),则可以调整整体的曝光值($s=r^\gamma$)。这里的指数参数$\gamma$就是曝光值。
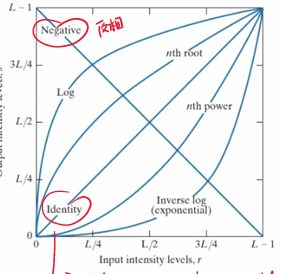
如果将曲线两头反向,则图片就会反相。
 |
 |
当然,你也可以只对一部分亮度的图像进行增强,其变换函数图像如下
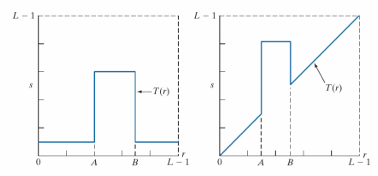
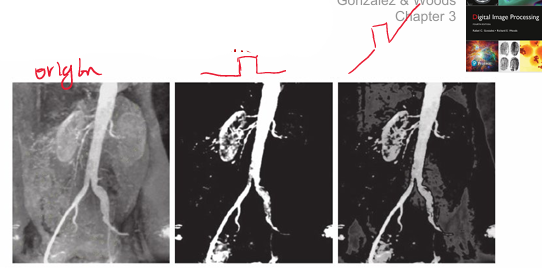
灰度变换-直方图处理
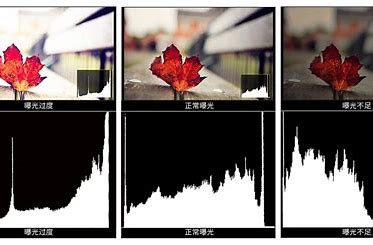
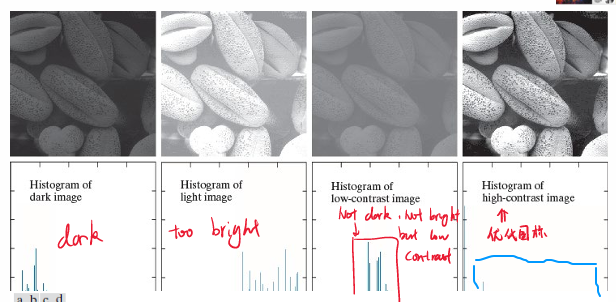
直方图用于统计一张图片中各值的像素点数量。其横轴为值,纵轴为数量。可以通过直方图看出来图像的整体亮度,直方图偏高代表图像中高亮度像素较多,偏低代表低亮度像素较多。
直方图均衡
从上面可以知道,直方图偏高或者偏低都有问题,能让它均匀分布才能创造不死黑,不过曝,对比度正常的图像,如下图。因此需要进行直方图均衡。
归一化的直方图
对于一个分辨率为MxN的图像,其值为$r_k$的像素个数为$n_k=h(r_k)$,则每个值出现的概率为
其中k为k个值,例如8bit图像k就位0-255。
这样就可以求到归一化的直方图,其实就是求到了图像像素值的概率分布函数,用连续函数的话来说就是概率密度函数(PDF)。
直方图均衡函数及其证明
那么有没有一种变换函数T,在对所有像素执行了$S=T(r)$之后,可以把左边这样的PDF转化为右边这样的均匀分布PDF呢?
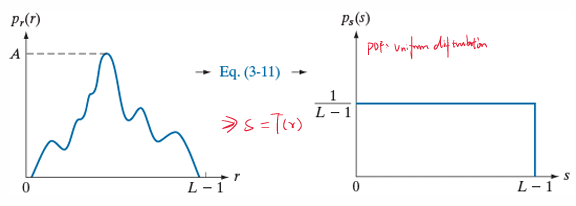
要想让它均匀,形象一点地理解就是分布得少的地方少动一点,把分布地多的地方往两边匀。如果使用概率分布函数(CDF)的值作为调整的系数,好像恰好就可以实现这一点。在分布较多的区域内,较低值CDF值较小,像素值会往小了调整;但是较高值的CDF值会陡然增大,此时像素值经过变换函数就会往大了调整。这样就实现了分布相似值的像素朝两边匀开。
因此有了下面这个函数:
其中$\int^r_0p_r(w)dw$就是求了当前像素值的概率分布函数。这个函数能使直方图均匀分布的数学证明如下:
首先,根据概率论有结论:如果$p_r(r)$和$T(r)$已知,$S=T(r)$,$T(r)$连续且可导,则有:
将$s=T(r)$对r求导:
上式写成倒数:
带入前面概率论得出的已知结论,因为值为r的像素点出现概率肯定大于0,即$p_r(r)>0$,所以$\frac{dr}{ds}$必然>0。因此下方绝对值可以直接去掉:
至此,证明了变换后的直方图各值分布密度$p_s(s)$是为$\frac{1}{L-1}$的常数。
直方图均衡函数和离散形式
连续形式:
离散形式:
在离散的情况下,求出来的理想$s_k$不一定有匹配的值,因此需要约成最接近的数。
离散直方图均衡计算例子
如下图,一张有8种灰度值,64x64分辨率的灰度图,其各值像素出现次数分别为$n_k$,将其直方图均衡。
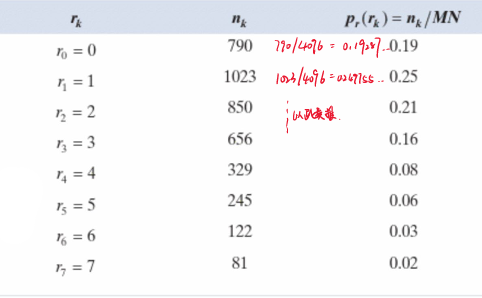
Step1:计算各值概率。该图共有$64\times 64=4096$个像素点。因此$p(r_0)=\frac{790}{4096}\approx0.19287$,以此类推。结果在上图。
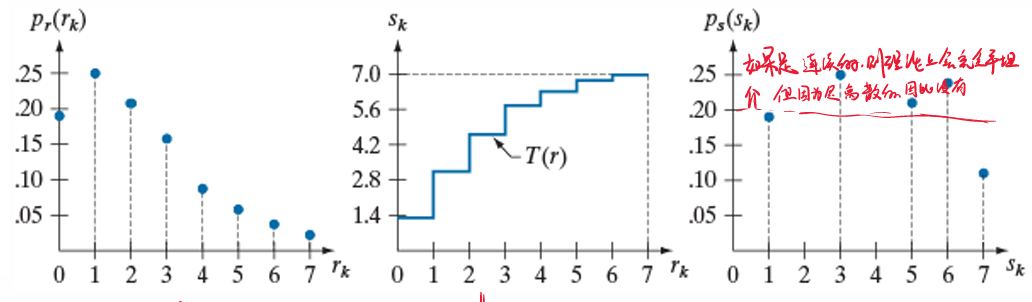
Step2:根据公式,将原有的值映射到新的值。例如值$r_1$被映射到$s_1$计算方式为:
以此类推,如下图

可以看到,原先分布薄弱的7被填充了多个数值。均衡化前后的直方图如下图所示。
直方图匹配
有些时候,并不希望将直方图完全变成均匀分布,而是有一个预设好的直方图“模板”,希望将任意一张照片的直方图变成这个模板这样的分布。这被称为直方图匹配。
直方图匹配函数
直方图匹配的原理是以均衡化的直方图作媒介,求得两直方图分布函数间的函数关系。
假设考虑灰度图像值$r$的PDF为$p_r(r)$,其被匹配后的输出为$z$,PDF为$p_z(z)$。如果我们将$p_r(r)$和$p_z(z)$套用前面提到的均衡化,并将$p_z(z)$的均衡化函数记为函数G,会得到:
因为他们均衡化后求到的s一致,因此有:$G(z)=s=T(r)$。把$G(z)$写成逆函数,有:
至此就拿到了直方图匹配函数。但是这一步逆函数,对于连续地解析表达式是非常非常难求的。但是所幸的是图像几乎都是离散值,对于离散量而言,将$r_k$计算为$s_k$,再将$z_q$计算为$s_q$,寻找$s_k$和$s_q$中最接近的,将$r_k$映射到$z_q$即可。
因此整个直方匹配函数离散操作为:
Step1:计算原始直方图和目标直方图的均匀化结果
Step2:建立一个look up table,将$s_k$和$s_q$中最接近的连在一起,可能存在多个映射到一个的情况。
Step3:根据上面得到的映射关系,将对应的$r_k$变成$z_q$。
直方图匹配例子
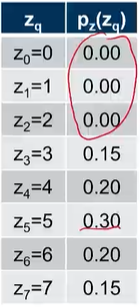
考虑直方图均衡化示例中的64 x 64的图像,$r_k$各值如下图左。目标直方图$z_q$各值在下图右。计算直方图匹配结果。
 |
 |
经过计算,这二者均衡化后的值如下表所示
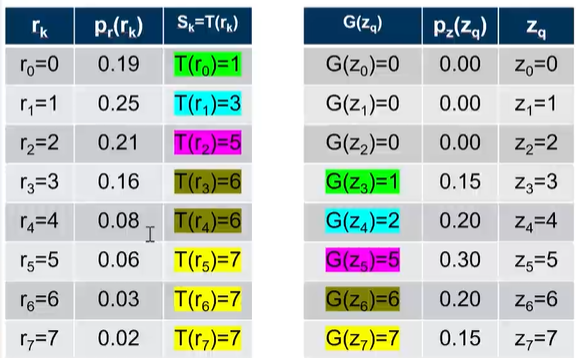
可以看到,上图中$s_k$和$s_q$值相等的都使用了相同颜色标注,他们是一一对应的关系。下一步就是:
- 将原先值为0($r_0=0$)的像素调整为值为3
- 将原先值为1的像素调整为值为4
- …
- 将原先值为3和4的像素都调整为6
- 将原先值为5,6,7的像素都调整为7
至此,便完成了直方图匹配。
空间滤波
图像处理的滤波也有空间滤波和频率域滤波。空间滤波通过把每个像素的值替换为该像素及其邻域的函数值来修改图像。空间滤波器可以实现图像的平滑、锐化、边缘增强等等。
空间滤波原理
空间滤波中有一个核(Kernel),这个核是一个矩阵。核矩阵在原始图像上滑动,将原始图像上对应的值挨个相乘,再把乘出来的结果加起来,得到新像素的值。如下图所示。
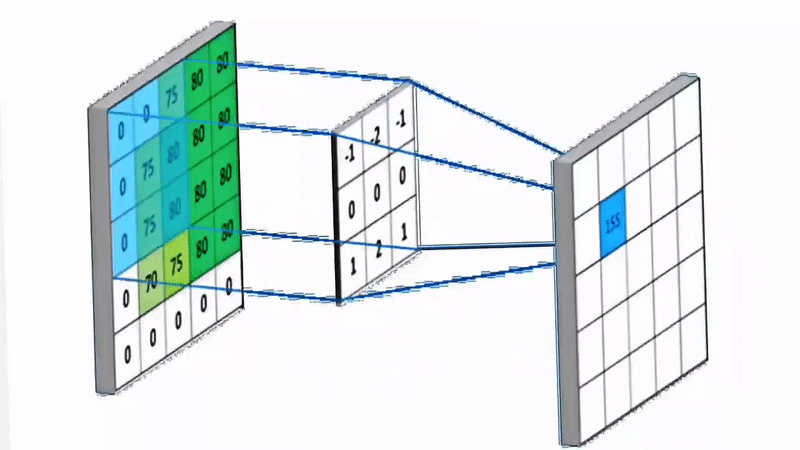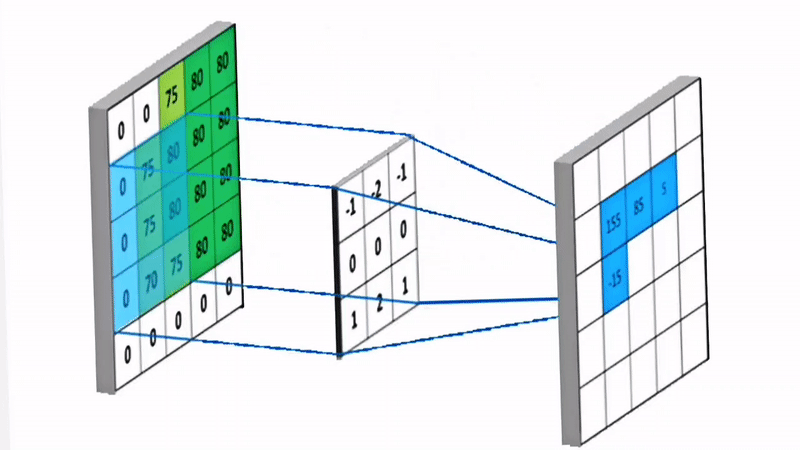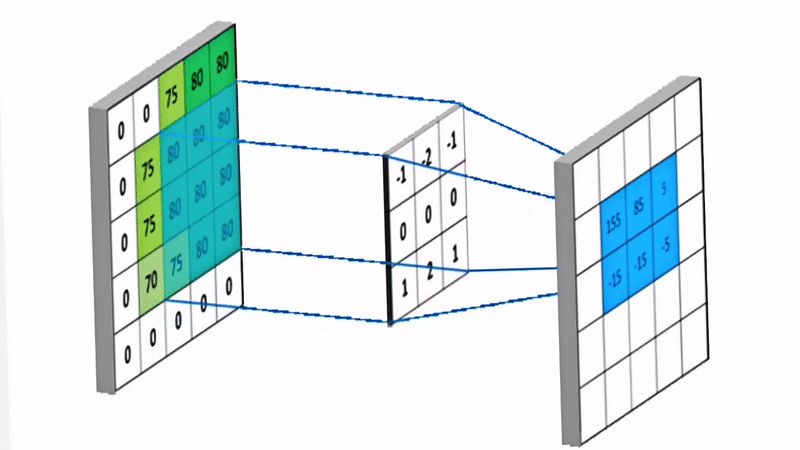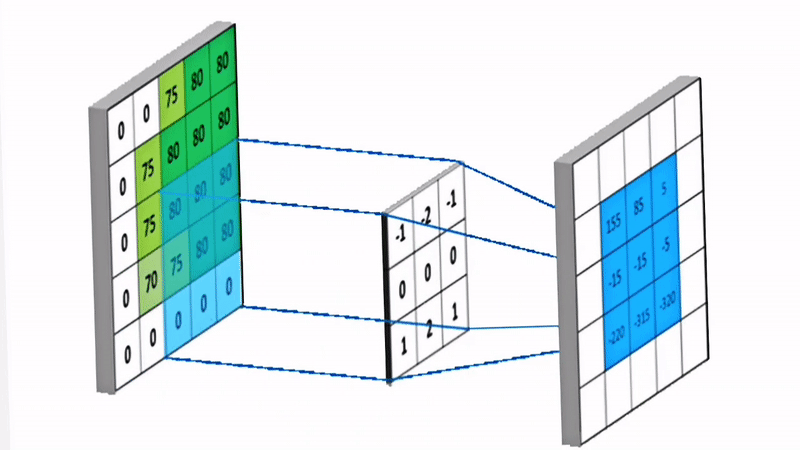
因为这个过程不涉及频域变换,因此被称为空间滤波,它是滤波器核与图像的卷积。空间滤波的数学表达式如下:
其中w为核矩阵,r为原始图像。
平滑(低通)空间滤波器
在前面DCT引入过一个概念:图像内邻接像素值变换速度越快,称为图像频率越高。而平滑滤波器会降低这样的急剧过渡,因此它是低通滤波器。
由于随机噪声通常表现为灰度的急剧过渡,因此平滑滤波器可以很好地消除随机噪声。同时平滑滤波器也会模糊图像,模糊的程度取决于滤波器核的大小和系数的值。
均值滤波(average filtering)
均值滤波就是求滤波器核内像素的均值。例如一个3x3的滤波器,那么该核每个元素的值就是1/9,这也称为盒式核
这样的结果就是,每个新像素的值都是周围8个像素的值和它的值的平均。平均之后原来的边界会变得不清晰,图像看起来会糊一层。因此它又叫均值模糊。

因为每个新像素都是原始一群像素的平均值,因此滤波后的新图像和原始图像各像素的均方差是最小的,即有:
其中a是原始图像像素值,$a_i$是变换后。
高斯滤波
盒式核对透镜产生的模糊特性(例如相机失焦)的模拟特性较差。但是高斯滤波器弥补了这一部分,可以产生很好的毛玻璃质感(win7用了都说好。
和之前讲的一样,高斯滤波的核函数来源于对二维高斯函数的采样,如下图
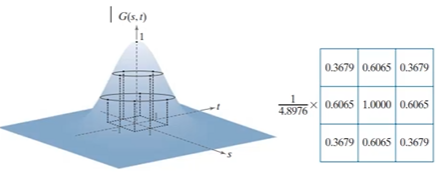
高斯模糊可以移除高斯噪声。与均值滤波相比,高斯模糊的边缘也更“柔和”。
统计排序滤波器(非线性)
中值滤波(median filtering)
中值滤波是将滤波核内所有像素的值顺序排列,然后选择中位数作为新的像素值。中值滤波只使用图像中原始存在的像素值,因此图像处理后会更接近于原图,而且因为边缘不会使用介于原始边缘差异之间的值的像素过度(例如黑白相交的边缘不适用灰过度,而是依旧从黑白里面选),因此中值滤波的模糊程度很小。
对于偶数个像素值,中值是最中间的两个取平均。
椒盐噪声(salt-and-pepper noise)又称脉冲噪声,它随机改变一些像素值,在二值图像上表现为使一些像素点变白,一些像素点变黑。 是由图像传感器,传输信道等产生的黑白相间的亮暗点噪声,也就是所谓“雪花”。

同时,由于中值滤波选中间值,而椒盐噪声一般是极大值或极小值,因此中值滤波对椒盐噪声可以很好地消除。下图从左到右是原始图像、均值滤波、中值滤波之后的结果。

中值滤波会让两图像像素值的绝对值差异最小,即
锐化(高通)滤波器
高通滤波器会强调图像变换较大的地方,对应的也就是边缘。因此高通滤波器会产生锐化的效果。