智能系统设计-Part1-GeneticAlgorithm

引入

GA简介

遗传算法（Geneic Algorithm, GA）是基于“物竞天择，适者生存”而提出的。它首先确定参数和优化目标，然后经历以下步骤来模拟这些参数的自然演化过程：

1. 随机地生成一些答案，称之为种群（Populaition）
2. 对他们进行评价
3. 选择较好的，作为parents（父母）
4. 使得父母重新组合（交叉）
5. 使得他们的孩子产生一些变异，随机地选择一些参数替代原有
6. 对他们产生的孩子进行评价
7. 剔除掉太差的，重复步骤3-7
8. 直到满足优化目标，“物竞天择，适者生存”的优化结束。

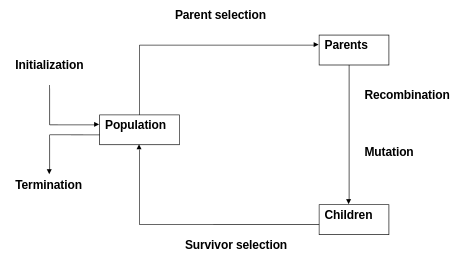
这整个步骤可以被简略概括为：选种-交叉-变异

基于GA的工作原理，以下方面都可以影响GA结果：

• Representation：对个体的表示，即，参数的选择（比如一个人，得有胳膊，有腿，有眼睛等等）
• Evaluation function (fitness function)：评价函数，用于“天择”
• Population: 种群
• Parent Selection Machanism: 父母选择机制
• Variation operators: 变异算子（包含交叉(crossover)和变异(mutation)）
• survivor selection mechanism (replacement): 幸存者选择机制

初始化和终止条件

在大多数遗传算法中，初始化只是简单的随机值。初始化是否值得额外的计算和算法在很大程度上取决于应用场景。

终止条件有很多种，但是其实他们大多数都无法保证结果达到最优，只有尽可能靠近。常用的终止方式有：

• 运行超过允许的CPU时间后停止
• 适应度超过给定阈值
• 在一段时间内，改善不明显
• 种群多样性在阈值以下

GA概念及常用算法

参数表达（Representation）

表型（phenotypes）：表型是基因型通过解码和表达所产生的实际特征或行为。在遗传算法中，表型通常是基因型经过解码后得到的解。

基因型（genotypes）：基因型是个体的遗传信息的编码表示。在遗传算法中，基因型通常表示为一个字符串或数组，其中每个元素代表一个基因，表型经过编码(encoding)即可得到基因型。

表型空间（Phenotype Space）：表型空间是所有可能的表型的集合，也就是解空间。

染色体（Chromosome）：染色体是基因型的一个具体实例。染色体通常表示为一个字符串或数组，其中每个元素代表一个基因（Gene）。

父母选择机制（Parent Selection Mechaism）

在当前评价机制下，高质量的个体会被给予更大的几率成为父母。靠后的个体也会被给予机会，只是概率不如高质量个体，也不是完全没有。

如果完全不给予靠后个体机会，则很容易陷入局部最优（local optimization）。

父母选择机制常用的有如下几种：

赌轮盘选择（Roulette Wheel Selection）

这种机制下，某一条染色体被选为父母的概率和它的评价函数的结果成正比。

1. 首先需要计算种群适应度的总和，下式中popsize为种群大小，$f$为评价函数 $$F=\sum_{i=1}^{popsize}f(v_i)$$

2. 然后用每个染色体自己的适应度/总适应度，得出该染色体被选中的概率

   $$p_i=f(v_i)/F$$

3. 接着求他们的累计概率，表达式如下图。这么做的意义是要将各个染色体按照自身的概率，在一条数轴上划分各段。

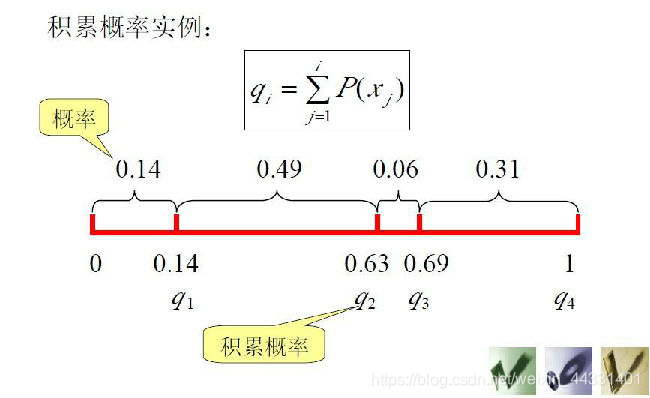
1. 然后按照均匀分布，随机生成一个r数落在0-1之间，根据这个数落入的区间选择出对上应的染色体$q_i$，遵循$q_{i-1}<r<q_i$。因为适应度越好的染色体占的空间也越大，因此这样选择出来的染色体和自身适应度正相关。

排序选择（Rank-based selection）

当适应度值差别很大时，轮盘赌选择就会出现问题。例如最优染色体的适应度值极高，占了90%以上的数轴，那么其他染色体被选择到的概率就很低。因此有另外一种根据适应度进行排序，再分配选择概率的方法。

以线性排序为例，最差个体排在第1位，最优个体排在第N位，根据排位先后，线性地分派给染色体i的选择概率。假设规定的最差染色体被选择概率为$n^-$最好为$n^+$，则每个被分配的概率为：

$$p(i)=\frac{1}{N}\bigg(n^-+(n^+-n^-)\frac{i-1}{N-1}\bigg)$$

除了线性排序之外，还有指数排序等。

锦标赛选择（Tournament-based selection）

锦标赛选择从种群中有放回地随机采样s个个体，选择其中最优的一个充当下一代父母。

通过对采样个数s改变可以调整选择压力。在s较大时，弱者被选中的概率会缩小。

交叉和变异（Crossover and Mutation）

相较于变异，交叉是一种更保险的优化。

交叉算子（Crossover Operator）

交叉算子有很多，这里只有PPT上提及的几种。

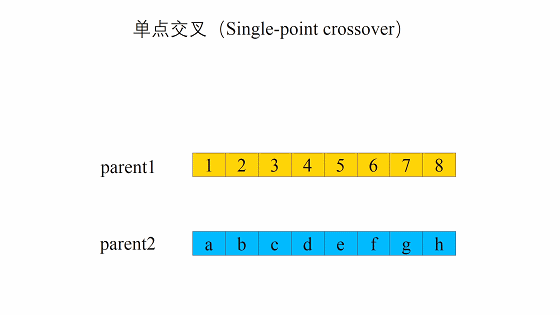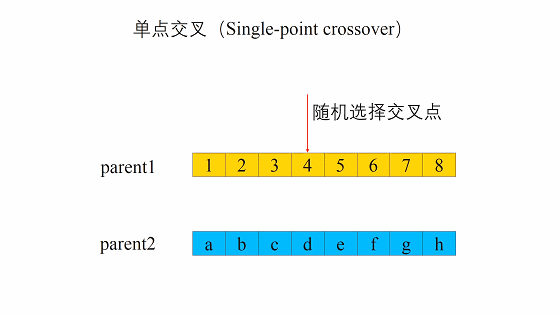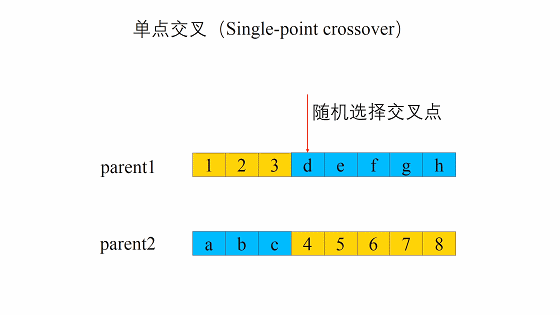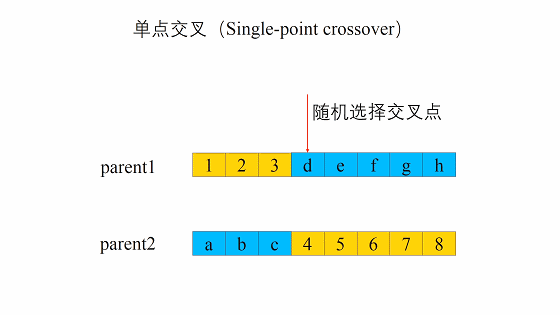
单点交叉（One-point Crossover）

这种交叉是随机产生一个数字（≤染色体长度）作为交叉位置。然后，保持该位置前基因不变，该位置后的基因换位。

举个例子，假设该随机位置为2：父母1：7 3 | 7 6 1 3；父母2: 1 7 | 4 5 2 2

单点交叉后：孩子1：7 3 | 4 5 2 2；孩子2：1 7 | 7 6 1 3

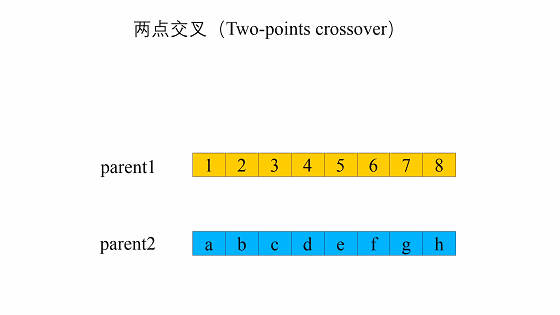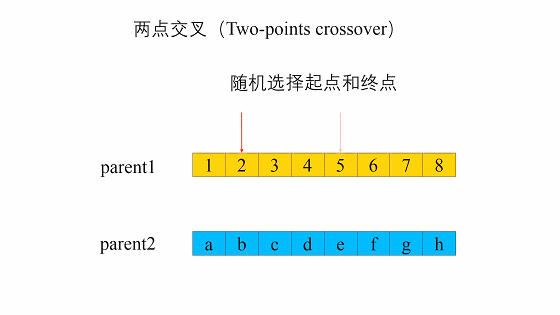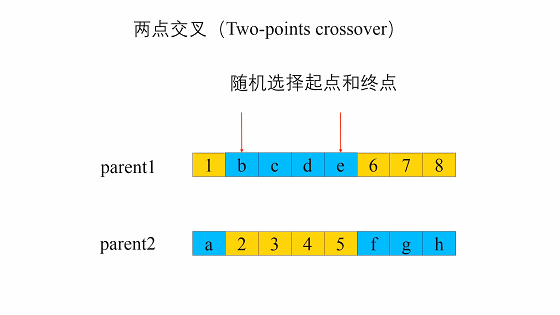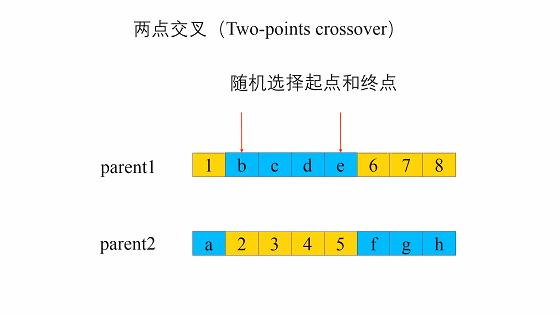
两点交叉（Two-point Crossover）

这种交叉与单点交叉类似，不同之处在于必须选择两个位置，并且只交换两个位置之间的基因。

举个例子，假设该随机位置为2，4：父母1：7 3 | 7 6 | 1 3；父母2: 1 7 | 4 5 | 2 2

两点交叉后：孩子1：7 3 | 4 5 | 1 3；孩子2：1 7 | 7 6 | 2 2

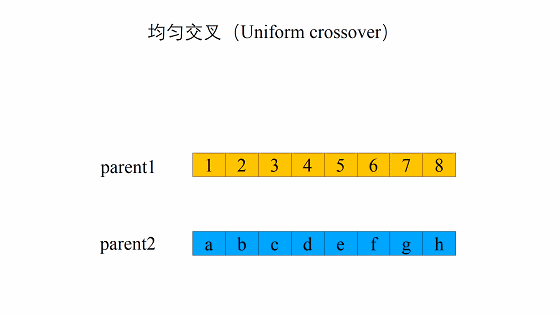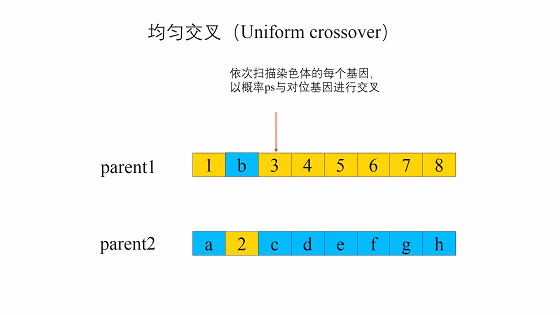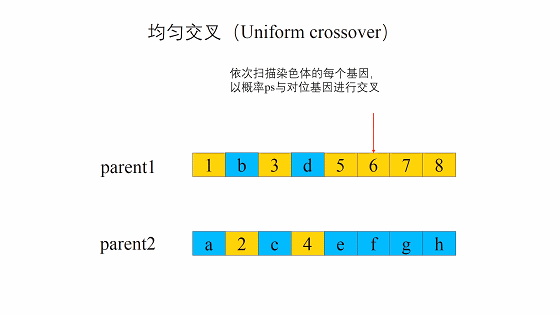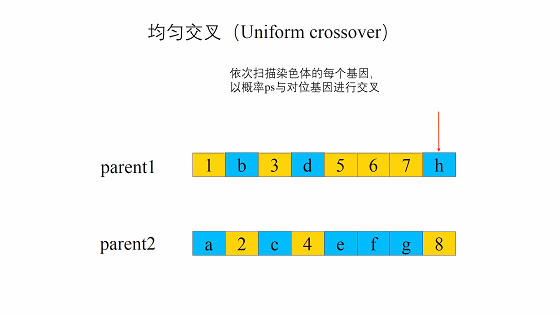
均匀交叉

遍历整个染色体，染色体中的每个基因都有一定概率与另一个染色体进行交叉。概率的代码实现可以是随机生成一个0-1之间的数，当该生成的数小于概率阈值时，不发生交叉，大于时，发生交叉。

倒置算子（Inversion）

将某个染色体上随机选择的两个基因交换顺序。这种操作来源于真实的生物进化。

例如：染色体为：3 8 4 8 6 7； 选择第二个和第五个，变异后为：3 6 8 4 8 7

变异算子（Mutation operators）

变异算子和均匀交叉类似，但是它是对bit的操作，它让染色体上的某一位bit有一定概率翻转。

淘汰机制（Survivor Selection Mechanism）

淘汰机制是用来保证不会出现一些“非法答案”。也就是那些错得太离谱的答案，需要通过淘汰机制淘汰掉。与上面的亲本选择机制不一样，这种淘汰机制是决定性的，并不会给低于这种阈值的个体人体机会。

这一步属于繁殖（Reproduction）。繁殖可以分为两种：世代复制（Generational Reproduction）和稳态复制（Steady-state Reproduction）

世代繁殖：在这种模式下，旧的种群会完全被新的种群顶替。根据当前的选择规则，会选出两个染色体为父母，经过交叉变异产生两个孩子，直到产生出N个孩子作为新的种群，新的种群将完全替代旧种群。因此如果共有N条染色体，该繁殖操作就会循环N/2次。

稳态复制：这种方法根据当前选择机制来选择两个染色体作为父母，同样地对他们交叉-变异来获得一个或者两个后代。但后续会将孩子重新放入原种群中，替换掉原种群中适应度较低的个体（具体替换取决于替换算法）；