时间延迟对系统频响的影响

时延是输入与控制系统开始响应输出之间的时间差，其被称为lag或者dead time，记作T或表示成$e^{-sT}$(拉普拉斯变换的时移性质：$L[f(t-t_0)]=F(s)e^{-st_0}$)

时延对频响相响图的影响

考虑一个系统函数为$G(s)$的一个系统，对其引入时间为T的时延，并求波德图

$G(s)e^{-sT}=|G(j\omega)|e^{\angle G(j\omega)}e^{-j\omega T}=|G(j\omega)|e^{j[\angle G(j\omega)-\omega T]}$

系统的幅频响应对应$|G(j\omega)|$，因此时延并不改变幅频响应。
但时间延迟从相频响应图中减去了$\omega T$，也就是说，随着频率增大，相位减少越大；换句话说，它削减了相位裕度。

如下图所示：

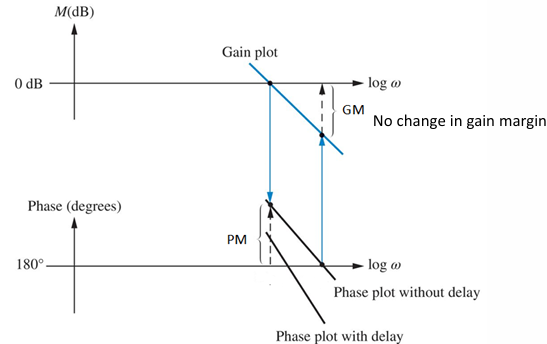
显然，如果时间延迟非常大，闭环系统将不稳定。

从时域的角度看

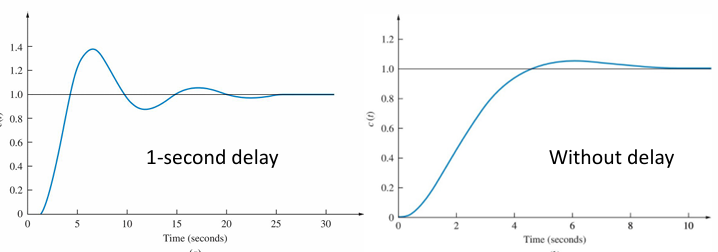
从时域的角度来看，延迟会造成（即，削减相位裕度会造成）

更低的阻尼比
更多的振荡响应

当系统内带有非最小相位元件(带有时滞特性/延时，相位滞后)元件时，会产生非最小相位系统。因此我们一般不单独讨论延迟，而是将其看做非最小相位系统来讨论。

非最小相位系统

什么是非最小相位系统

非最小相位系统（Nonminimum-Phase (NMP) Systems）是在复平面的右半平面（RHP）上具有零点，但系统仍旧稳定（极点还在左侧）的系统。由于根轨迹总是趋近并收敛于零点，因此当增益大到某一点，右半平面的零点有使系统极点趋向右半平面的趋势，可能造成系统不稳定。

（补充）反之，最小相位系统(Minimum-Phase (MP) Systems)就是s域右半平面没有零点或者极点的系统。最小相位系统无论何时都是稳定的。

在具有相同幅值特性的系统中，对于大于零的任何频率，最小相位系统的相角总小于非最小相位系统；例如下图，是$G_1(s)=10\frac{s+1}{s+10}$（MP system）和$G_2(10\frac{s-1}{s+10})$(NMP system)的幅频图相频图。

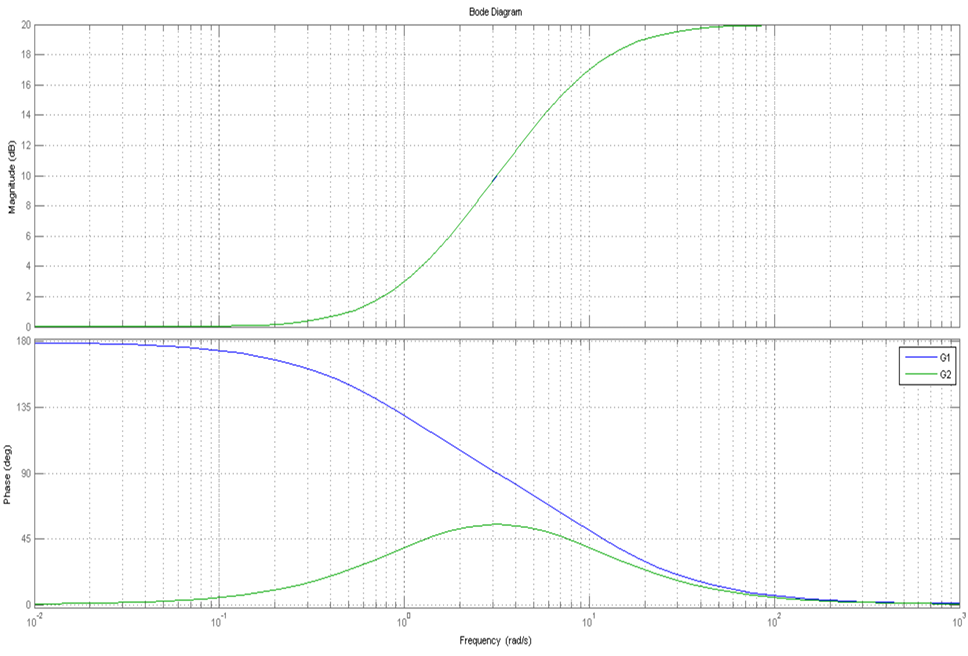
从单位阶跃响应看最非小相位系统-负调

参考资料：自动化学报

一般情况下, 非最小相位系统对阶跃输入信号具有负调(Overshoot, 或称为下冲) 响应。下冲意味着阶跃输入的暂态响应一开始朝阶跃输入的相反方向运动

下图展示了传递函数为$G(s)=\frac{(s-1)^2}{(s+1)^3}$的单位阶跃响应。

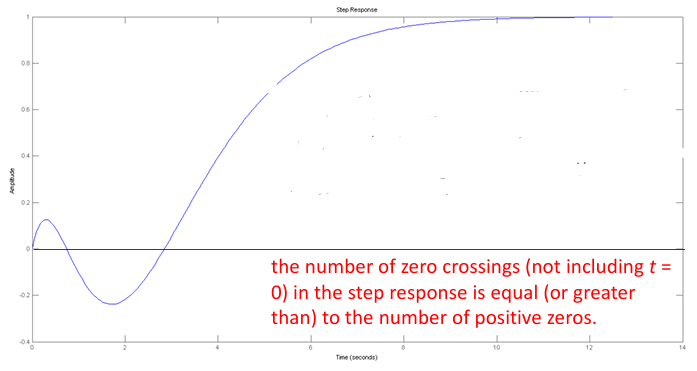
对于非最小相位系统而言，其单位阶跃响应穿过0的次数（不包含原点）大于或等于右半平面零点的个数。例如上图，右半平面零点有两个，都是1，因此穿越两次0。

但是，当一个线性非最小相位系统含有非实零点时, 其阶跃响应并非一定具有负调特性（可能还是有）。如传递函数$G(s)=\frac{s^2-s+4}{(s+3)^3}$描述的非最小相位系统对阶跃信号的响应就是单调的, 没有负调特性，如下图所示。

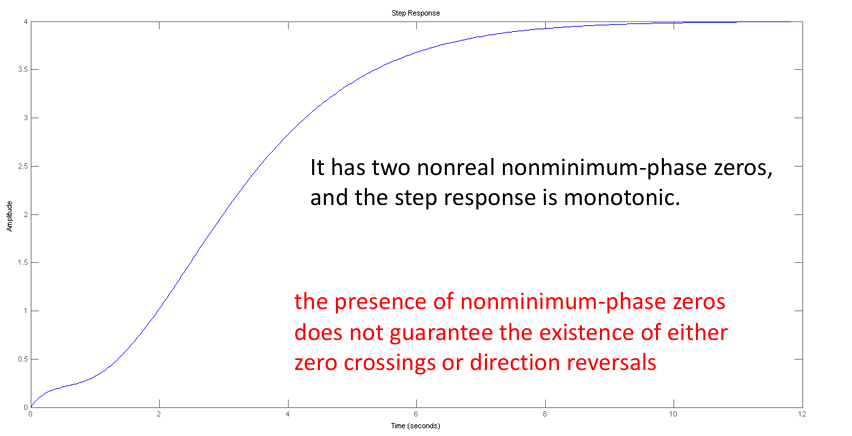
对于非线性非最小相位系统, 其阶跃响应一般具有负调特性,但因其种类繁多,无法用统一的定理来判定其负调响应的类型。

PID控制器

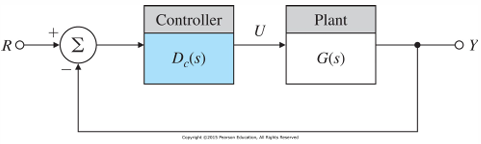
PID控制器是一种利用比例（Proportional）、积分（Integral）和微分（Derivative）三种动作来根据误差信号调节系统输入的反馈控制器。因为是调节系统输入，PID控制器一般作用于系统函数之前，和系统函数一起构成新的经过修补的前向传输函数。

PID控制器的通用式可以表达为（分别对应比例部分，积分部分，微分部分）：

$c(t)=K_p[e(t)+\frac{1}{K_i}\int_0^te(t)dt+K_D\frac{de(t)}{dt}]$ $C(s)=K_p\bigg(1+\frac{1}{K_is}+K_ds\bigg)$

而所谓调PID，其实就是去调$K_p,K_i,K_d$这三个系数。下面会详细介绍

拆分研究

P控制器

只保留P控制器的话，那就相当于给了一个增益，即$C(s)=K_P$，它和系统级联构成的就是$K_PG(s)$。单看这个控制器，它相当于把原来输入系统函数的$e$（$e$是输入与当前输出的差）放大成了$K_Pe$。

下图展示了P控制器下，控制器的输入$e$和其对应的输出（即输入给$G(s)$的输入）：

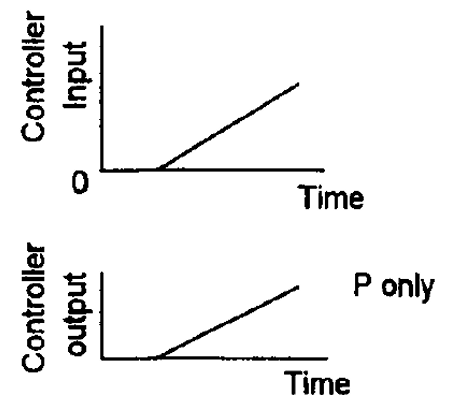
比例控制存在着一些不足——无法消除稳态误差。

假设系统$G(s)$自带稳态误差，那么对于单位阶跃信号（推导见CH1)：

$e_{ss}=\frac{1}{1+\lim_{s\rightarrow0}{K_PG(s)}}$

可以看到因为原系统$\lim_{s\rightarrow0}{G(s)}\neq\infty$，$K_p$只是减小了稳态误差，没有完全消除。

I控制器

I控制器就是积分的部分，其s域为$C(s)=\frac{K_i}{s}$。该控制器会将$e$进行积分，即控制器输出为$K_i\int edt$，如下图。

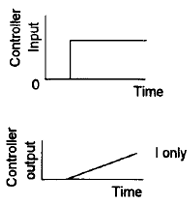
由于这个积分项会将前面若干次的误差进行累计，所以可以很好的消除稳态误差。从数学推导的角度来解释一下：

假设系统$G(s)$自带稳态误差，那么对于单位阶跃信号

$e_{ss}=\frac{1}{1+\lim_{s\rightarrow0}{\frac{K_i}{s}G(s)}}$

此时分母这个$s$会使得后面这一项趋于无穷，进而导致$e_{ss}=0$

D控制器

D控制器是微分的部分，其s域为$K_ds$，即该控制器会对误差进行微分，求出误差的变化速率：$de/dt$。下图展示了控制器输入与输出关系

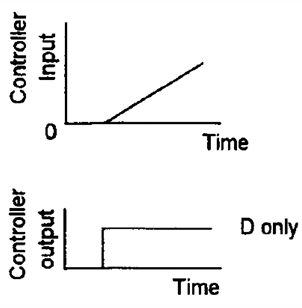
微分控制器不会影响稳态误差，因为在稳态误差发生时，$e$已然达到稳定，误差随时间的变化率为零，因此微分控制器在此时并不起作用。

不同控制器多项结合

PI控制器

$C(s)=K_p(1+\frac{1}{K_is})$

P控制器只能减少不能消除稳态误差，而I控制器可以完全消除稳态误差。因此这二者结合的控制器稳态误差被I消除，没有稳态误差。
给系统的分母引入了一个$s$，削减了系统的高频（s很大）增益，而噪声通常是高频的，因此削减了噪声的影响
在分母引入$s$，相当于加快向量负半虚轴的增量；同时削减高频增益还使得幅度穿越频率变得更靠前。二者综合，即，减小了相位裕量。

控制器波特图如下：

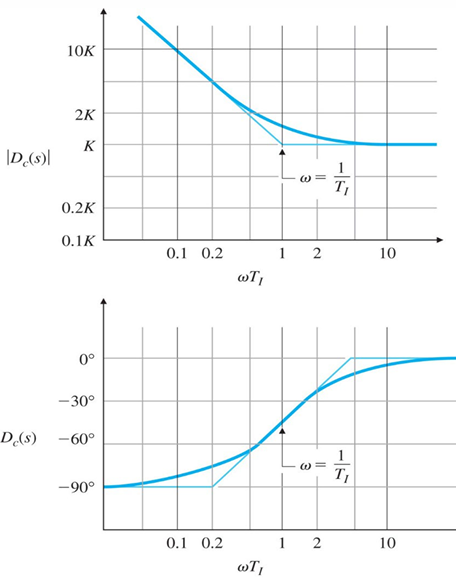
PD控制器

$C(s)=K_p(1+K_ds)$

给分子引入一个s可以略微降低低频增益并提高高频增益。使得穿越频率靠后，增加相位裕量。
但是也增加噪声对系统的影响，因为噪声往往是高频的。

控制器波德图如下：

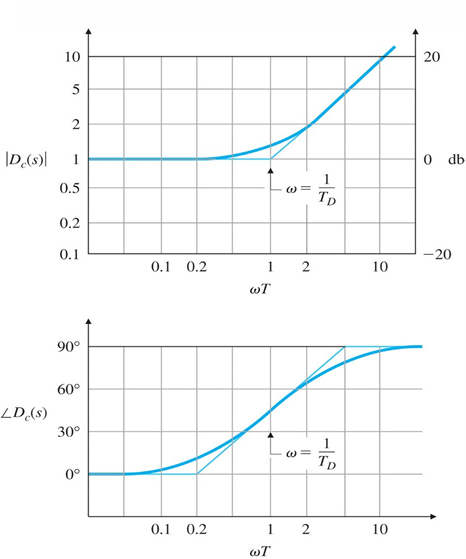
PID控制器

标准形式：

$C(s)=K_p\bigg(1+\frac{1}{K_is}+K_ds\bigg),T_i=\frac{K_p}{K_i},T_d=K_dK_p$

并联形式：

$C(s)=K_p+\frac{T_i}{s}+T_ds$

结合所有三种控制模式（比例、积分和微分），可以生产出没有稳态误差并减少振荡趋势的控制器。在后面Part2会介绍PID调谐原则，即如何调整$K_p,K_i,K_d$。