Part1-CH2-电路实现技术
使用 AND OR NOT门综合设计(Synthesis Using AND, OR, and NOT Gates)
Minterm: 选取为1的项目。 选择输入逻辑满足F=1的输入组合,通过以下步骤设计Boolean function:
使得某一个输入满足组合时输出为1(输入进行AND运算)
当 1 中任意一个满足时(步骤1的结果们进行OR运算),输出为1
例如,对$x_1,x_2,x_3$三个输入,想要满足$x_1=1 x_2=1 x_3=1$ 和$x_1=0 x_2=1 x_3=1$ 时输出为1,首先选取使得f输出为1的组合,也就是前面提到的两个,然后进行and运算:$x_1x_2x_3$和$\overline x_1 x_2x_3$,再对and运算的结果进行OR运算$F=x_1x_2x_3+\overline x_1 x_2x_3$(对应 Sum of Product SOP)
Maxterm: 排除为0的项目。选择输入逻辑满足F=0的输入组合,通过以下步骤设计Boolean function:
使得输入满足这个组合时输出为0(输入AND运算的结果取反,然后德摩根化开,此时$\overline {A.B}$ 就会变成$\overline A+\overline B$ )
当所有输入情况任意一个满足为0时为0,否则为1(步骤1的结果AND运算)。
例如: $F=(A+B).( \overline {A} +B).(A+ \overline {B} )$ (对应 Product of Sum POS)
Cost:电路中 门的总数 加 门的输入信号的总数, 如果题目说需要同时给了未取反和取反(complement)的形式,则可以忽略not门造成的cost,否则需要计算not门的cost
例: Maxterm的化简
把AND OR NOT门电路转化成NAND和NOR只需要用DeMorgan’s theorem 整体取反后化开即可。Multiplexer后面有更详细的涉及,此处省去。
晶体管开关 (Transistor Switches)
晶体管有三个级: 源极(Source) 漏极(Drain) 栅极(Gate)
NMOS: 当$V_G$是低电平的时候关断,高电平的时候导通。
PMOS: 当$V_G$是低电平的时候导通,高电平的时候截止。
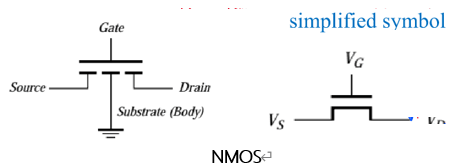

NMOS 逻辑门
利用开关的特性,通过上拉或下拉工作模式即可实现一个基于NMOS的逻辑门。此时需要一个限流电阻。因此该种方式功耗较大
从MOS管的构成视角来看,AND和OR门其实是NAND和NOR门取反(如下图所示),成本更高
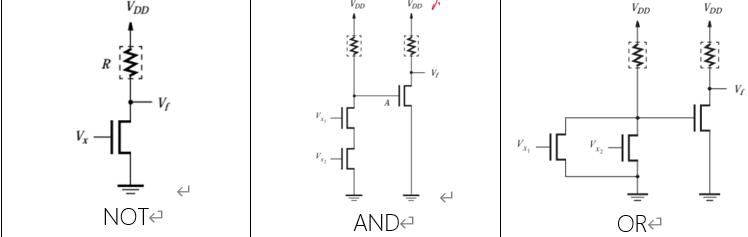
CMOS逻辑门 (五星级的)
CMOS逻辑门的介绍
NMOS逻辑门中通过上拉电阻实现上拉电路,这导致了功耗增加。CMOS逻辑门则优化了这个问题。
CMOS使用上拉电路和下拉电路,构成逻辑门。以NOT门为例,无论输入是低或高时,CMOS NOT门都直接被连到VCC或者GND,内部没有电流流动,理想状态下没有功率。这是CMOS是当今最流行的逻辑电路技术的原因。
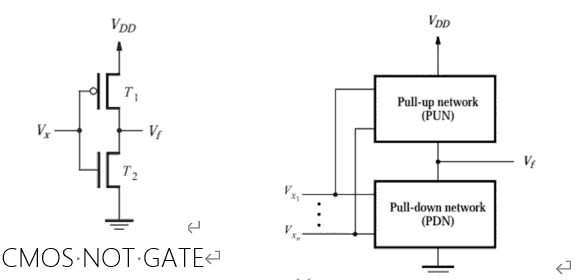
使用CMOS逻辑门构建逻辑电路
在MOS层面,AND逻辑需要两个MOS都导通才导通,因此可以用两个MOS管串联来实现;OR逻辑只需要任意任意一个MOS导通它就导通,因此可以用两个MOS管并联来实现
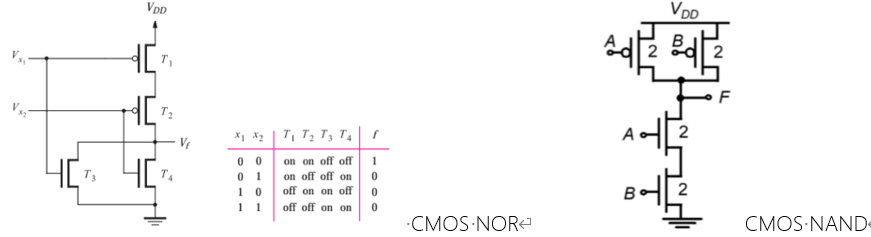
下图就时一个使用MOS管实现NOR逻辑的例子:
上拉电路是电路取1的表达状态:根据真值表,只有当$x_1,x_2$都是0的时候,电路输出才是1。也就是$x_1x_2$
下拉电路是电路取0的表达状态,根据真值表,只要任意输入不为0,电路输出0。也就是$x_1+x_2$
- 根据上面的分析,AND逻辑使用串联,OR逻辑使用并联,即可得到下面这个NOR gate
Example:Realise the following function using PMOS and NMOS$f= \overline {x_ {1}} + \overline {x_ {2}} \cdot \overline {x_ {3}} $
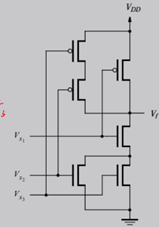
如上图所示,上拉电路为$f=1$的时候,也就是$f= \overline {x_ {1}} + \overline {x_ {2}} \cdot \overline {x_ {3}} $
下拉电路为$f=0$的时候,也就是$ \overline f=\overline { \overline {x_ {1}} + \overline {x_ {2}} \cdot \overline {x_ {3}} }=
( x_ {1} ) (x_ {2}+x_ {3}) $,逻辑是($x_1$) 与 ($x_2,x_3$并联的结果) 串联
可编程逻辑器件 (Programmable Logic Devices PLDs)
Programmable Logic Array (PLA)
PLA 由AND运算后输入给OR运算,整体构成了一个SOP的形式,下图中曲线的位置代表它可编程。
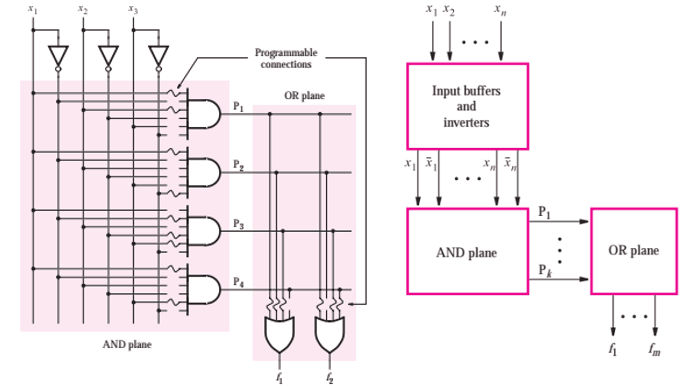
下图逻辑表达式如下
$ P_ {1} $ = $ x_ {1} $ $ x_ {2} $ $ P_ {2} $ = $ x_ {1} $ $ \overline {x}_ {3} $ , $ P_ {3} $ = $ \overline {x}_ {1} $ $ \overline {x}_ {2} $ $ x_ {3} $ , $ andP_ {4} $ = $ x_ {1} $ $ x_ {3} $
$ f_ {1} $ = $ x_ {1} $ $ x_ {2} $ + $ x_ {1} $ $ \overline {x}_ {3} $ + $ \overline {x}_ {1} $ $ \overline {x}_ {2} $ $ x_ {3} $
$ f_ {2} $ = $ x_ {1} $ $ x_ {2} $ + $ \overline {x}_ {1} $ $ \overline {x_ {2}} $ $ x_ {3} $ + $ x_ {1} $ $ x_ {3} $
PLA 所需的可编程开关具有难以制造,速度慢的问题。
Programmable Array Logic (PAL)
PAL的AND plane是可编程的,OR plane是固定的。与PLA相比,PAL提供的灵活性较小;PLA允许每个或门最多有四个乘积项,而PAL中的或门只有两个输入。但它减少了可编程开关的数量。
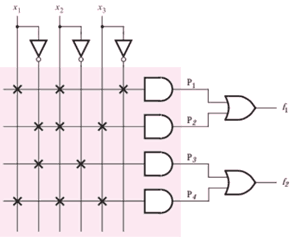
上图的输出为: $ f_ {1} $ = $ x_ {1} $ $ x_ {2} $ $ \overline {x}_ {3} $ + $ \overline {x}_ {1} $ $ x_ {2} $ $ x_ {3} $ ; $ f_ {2} $ = $ \overline {x}_ {1} $ $ \overline {x}_ {2} $ + $ x_ {1} $ $ x_ {2} $ $ x_ {3} $
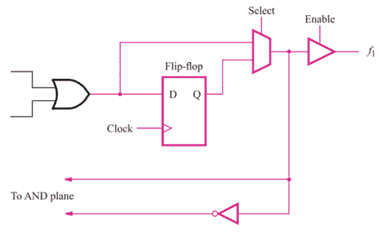
因为PAL的OR的输出是不可编程的,因此flexibility较差。利用额外的宏单元来提升flexibility。宏(Macrocell) :将OR Gate的输出连接至额外的电路,如下图例子所示。
Complex Programmable Logic Device (CPLD)
为了实现需要更多输入和输出的电路,可以使用多个PLA或PAL,或者可以使用更复杂类型的芯片,称为复杂可编程逻辑器件(CPLD)。CPLD的基本结构可看成由可编程逻辑阵列(LAB),可编程I/O控制模块和可编程内部连线(PIA)等三部分组成。
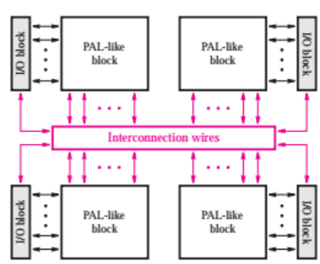
Example:下图是四个类似PAL的块,连接到一组互连线。每个类似PAL的块也连接到标记为I/O块。note: 一旦CPLD被编程了,那它的程序是可以断电保存的。
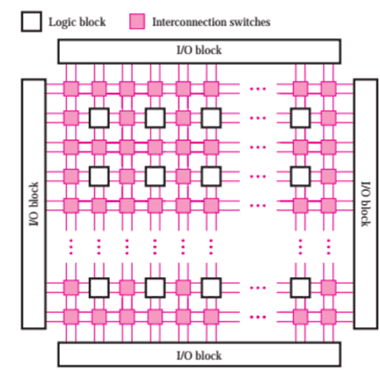
Field-programmable gate array (FPGA)
FPGA由可编程逻辑块(CLB/Logic Block),输入/输出模块(IOB)及可编程互连资源(PIR)等三种可编程电路和一个SRAM结构的配置存储单元组成。
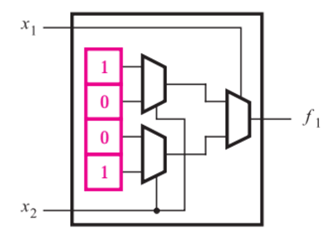
最常用的可编程逻辑块(Logic Block),是查表(Look Up Table LUT)
Custom Chips, Standard Cells, and Gate Arrays
限制PLD中可以容纳的电路大小的关键因素是可编程开关的存在。尽管这些开关提供了用户可编程性的重要优势
它们在芯片上消耗了大量空间,从而导致成本增加。
它们还导致电路运行速度的降低
以及功耗的增加。
AISC可以解决如上问题
Application-specific integrated circuits (AISCs)
专用集成电路,是指应特定用户要求和特定电子系统的需要而设计、制造的集成电路。制造商首先制造出逻辑操作的模板,后根据用户需求将模板用不同方式组合在一起。
ASIC在批量生产时与通用集成电路相比具有体积更小、功耗更低、可靠性提高、性能提高、保密性增强、成本降低等优点。
ASIC和FPGA相比,ASIC是专用集成电路,一旦设计完成后集成电路即固定。而FPGA是在阵列内集成大量数字电路基本门电路和存储器,开发人员可以通过烧写FPGA配置来定义电路。
一个AISC的例子:这个电路中,制造商制造框起来的标准逻辑块,用户自定义连接(红线),来实现不同输出,下图电路实现的输出就是:$f_1= x_ {1} x_ {2} + \overline {x_ {1}} \overline {x_ {2}} x_ {3} + x_ {1} x_ {3} $; $ f_2= \overline {x_ {1}} \overline {x_ {3}} + \overline {x_ {1}} \overline {x_ {2}} x_ {3} + x_ {1} x_ {3} $

传输门(Transmission Gates)五星级
NMOS(高开低关)传输0较好,而传输1较差。PMOS(低开高关)传输1较好而传输0较差。传输门把一个NMOS和一个PMOS组合在一起,从而实现很低的导通电阻和很高的截止电阻。因此,传输门可以直接使得原始信号x通过逻辑门,此时逻辑门输出$f=x$。
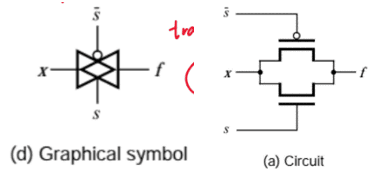
五星级问题:一个传输门有几个 Transistor? ——2个; 因为是把PMOS和NMOS组合在一起
五星级例题:使用传输门构建XOR
XOR表达式:$f=\overline x_1x_2+x_1 \overline x_2$
根据真值表,当$x_1=0$时,输出$f=x_2$。当$x_1=1$时,输出$f=\overline x_2 $。根据传输门良好导通的特性,下图电路可被设计。
 |
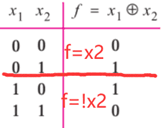 |
SPLD、CPLD和FPGA的实现细节
PLD
这是一个普通的XOR Gate,使用NMOS实现的电路
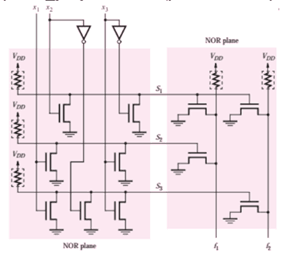
这是可编程版本
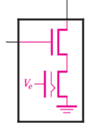
白色框框内部结构是EEPROM编程开关,$Ve$连接的就是EEPROM
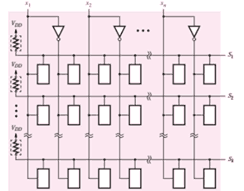
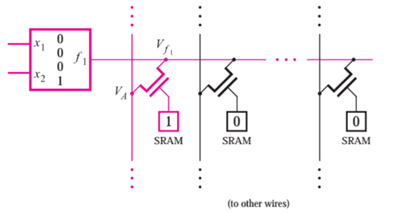
FPGA
与白色框框不同,FPGA采用SRAM编程,结构如下图所示. SRAM 单元中的数据掉电就会丢失
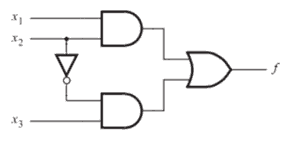
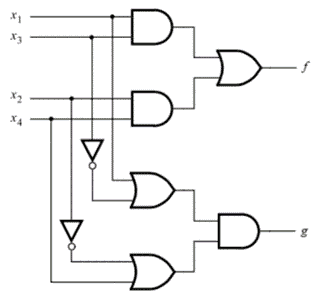
典型逻辑电路和它们的VHDL代码
例1:
1 | --定义实体,主要定义输入输出的端口-- |
例2:
1 | ENTITY example2 IS |