Part1-CH3-数字电路的化简
最小化策略
基本概念
包含名词:
Literal: 字符,也就是有几个输入变量
Implicant: 蕴含项,输入变量的不同组合,也就是卡诺图里面的圈,一个圈就是一种蕴含项。
Prime implicant: 质蕴含项就是不能与其它蕴含项合并的蕴含项, 也就是,这个卡诺图的圈无法被更大的圈包裹.
Cover: cover是不同implicant的组合,就是不同卡诺图的圈组合成的完整的表达式。
Cost: 电路中所有 门的数量 + 门的输入信号的数量
Essential prime implicant: 若函数的一个质蕴涵项包含有不被函数的其他任何质蕴涵项所包含的最小项,则此质蕴涵项被称为必要质蕴涵项。
举个例子:
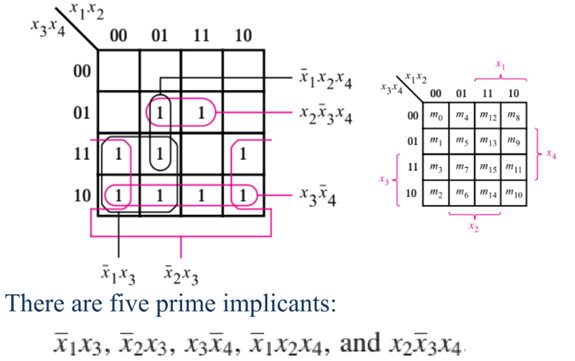
$\overline x_2 x_3$就是一个essential prime implicant, 因为$m_{11}$没有被其他任何质蕴涵项包含。同理还有$x_3 \overline x_4$ 和$x_2 \overline x_3 x_4$.
在最少的cost的布尔方程里面,必要质蕴涵项是必须被包含的。写出必要质蕴涵项之后,发现$m_7$还没有被包含到。$m_7$可以被$\overline x_1 x_3$或者$\overline x_1 x_2 x_4$包含,取其最小成本$\overline x_1 x_3$,所以这个布尔函数最小cost是:
因此,寻找最小cost电路的步骤是:
- 写出$f$的所有质蕴含项*
- 找到所有必要质蕴涵项
- 如果必要质蕴含项就包含了函数的所有1状态,那这就是最小cost,如果没有,则需要添加cost最小的非必要质蕴涵项来覆盖所有1状态
多输出电路(Multiple-Output circuits)
在具有多个输出的电路中,让电路共享一些逻辑门可以有效减少cost
这要求在卡诺图化简中并不一定按照质蕴涵项去画圈,而是查看更多蕴含项,寻找相同的蕴含项。
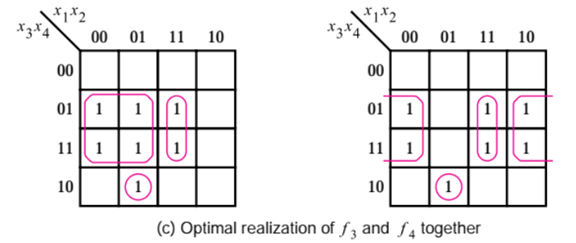
如上图就有两个蕴含项可以被共享。CAD工具将会自动执行这个共享的过程。在人工设计(考试)的时候,多输出电路也可以通过尽量圈出可以共享的圈圈来减少cost
多级综合(Multilevel Synthesis)—不考
Fan-in (扇入): 一个逻辑门输入的数量
Fan-out(扇出): 是指该模块直接调用的下级模块的个数。也就是一个逻辑门的输出连了几个下一级门。
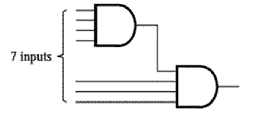
通常来说,使用CMOS制造的芯片存在扇入限制。通常希望AND门扇入小于5。可以使用分配率,把一层极的计算化成多个层级。下图就是两个例子
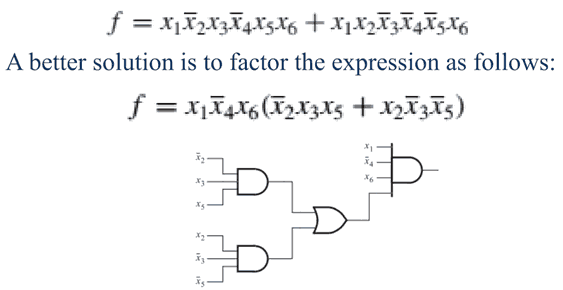 |
 |
立体表示法(Cubical Representation)
卡诺图能表示的函数大小受到限制,为了处理更大的函数,需要使用立方体表示。
构造立方体
有几个变量,就需要构造一个几维的立方体。立方体的顶点代表不同变量组合,立方体的边必须是含有一个x的组合,x代表0或者1。而面是含有两个x的组合。
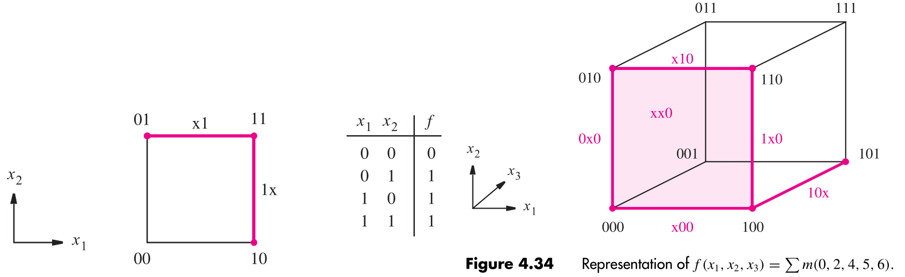
以这个三维的cube为例,首先标注顶点,000为顶点开始的三条边(三个变量所以三条边,x在三条边上换3个位置)需要分别为00x,0x0,x00,这三条边连接的另一个顶点将会是001,010,100(也就是x取和000相反的情况)。然后将新的顶点以同样的规则向外延伸,直至构成立方体。
化简
$f={000,010,100,101,110}$,将函数表达出来,并在顶点处标注出来。上图中的顶点围成了一个面和一条线,这个面是xx0,这条线是10x,所以这个函数可以被化简成
四维立方体:
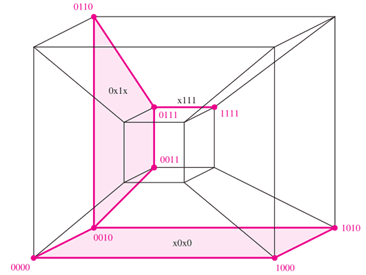
四维立方体可以画成在一个大立方体内囊括了一个小立方体。这样每个顶点都有4条支路,可以安装上面的方法标注顶点了。
表格法化简(Quine-McCluskey 法)
Step1 – 计算质蕴涵项
- 首先,把minterm表达式的项按只含0个“1”,只含1个“1”,只含2个“1”,…,只含n个“1”(n为变量个数)划分为不同的Group,并按“1”的数量排列(升序或降序均可)成表
- 准备一张新表。从含有最少数量的“1”的Group开始依次向下,将当前Group中的每一项与下一个Group的每一项比较。若两者只有一个变量不同,则将两项提取出来,并将不同的变量处用x标记,生成一个新的项。如果新的项在新表中已存在,则不执行动作;若不存在,则将这个新的项放到新表中的相应Group中。最后,在原表的两个Group中将提取的两项对应的“Subcube Covered”打上标记(打√)
- 在新生成的表中,重复2,直到新表中不存在只有一个变量不同的项为止
- 所有未被打√的项,就是质蕴涵项。
例如:$f_{(x_1,…x_4)}=\sum m(0,4,8,10,11,12,13,15)$
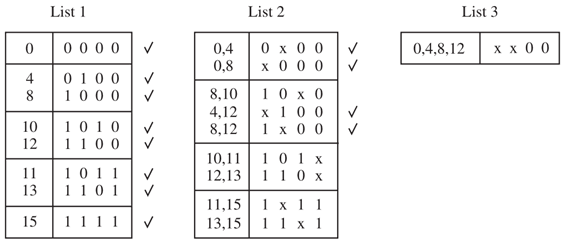
所以这个表达式的质蕴涵项就是
Step2 – 找到必要质蕴含项
把step1中找到的质蕴涵项列成表,如下图。发现0和4只有xx00表达了,所以xx00是必要质蕴涵项。把$P_6$挑出来
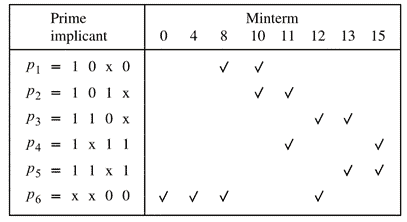
Step3 – 找到最小成本非必要质蕴涵项
移除p6和被p6表达的0,4,8,12(被挑走了),得到下表
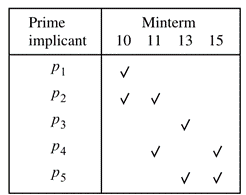
可以看到p1和p2的cost是相同的(他们都只有一个x),但是p1只能表述10, p2可以表述10,11,因此称p2支配 (dominates) p1。因此在这里选择p2。同理,可以选择p5。可以看到p4已经被p2和p5表达,因此这是不必要的。

Step4 – 完成化简
取step2的必要质蕴含项,step3选取的之蕴含项,
所以,化简后:$C={p_2,p_5,p_6 },f=x_1\overline x_2 x_3+x_1 x_2 x_4+\overline x_1 \overline x_3$