电信传输理论-CH5-金属传输线理论

引入

这一章的传输理论知识和实例分析都非常重要。

• 一条传输线中，波的参考的起始点称为“The driving point”，该point非传输线的头尾两端。因为在研究传输线时，研究的不是它的头尾，而是中间这一部分的特质。头尾需要单独讨论。

• 我们认为传输，是在远距离尺度上的。因此需要主要关注传输线上的时间差等。同时，由于干扰，传输线频率选择性衰减等因素，发射出去的放波会失真，在时域展宽等。

• 只有在长线分布下，才认为线内的电容，电阻等是均匀分布的。

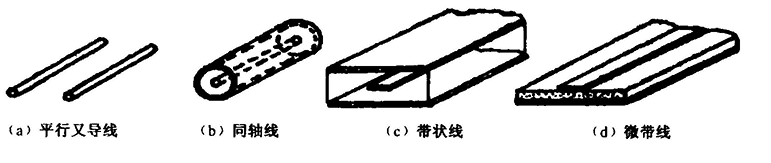
常见的金属传输线有上图4种，其中，平行双导线的英文是 twin-wire。本章节主要研究平行双导线，其他的简略。平行双导线随着传输的工作频率增高，其辐射损耗会急剧增加，故这种传输线只适合于1000米波至大于10米波的低频段。

金属传输线（主要以双线为例）

双线（twin-wire），是指的由两条传输线线构成一个完整的传输系统，如下图所示。

最典型的双线就是双绞线。双绞线也是金属线传播的一种典例，大部分金属线与双绞线分析方式类似。

在本课ch3中简略介绍过双绞线，在分析双绞线时，我们以微积分的概念将其切分，认为它们是平行的。在前面是对双绞线的感性认知，这一部分会更深入地学习。

bnh科普小课堂：虽然看起来现在无线通信，光通信使用远比金属传输线广，但是AI军火商NVIDA认为，在极短距离传输下（芯片内部），金属传输先比现有的光通信更有优势。因此金属传输先仍有很大研究价值

1234123

bnh科普小课堂：在金属线中让电磁波泄漏：回想一些LRC震荡电路，在理想情况下，这种电路会在线路内无限震荡。但如果在线上开一个口子，那么电磁波便会辐射出去。无线通信使用天线来开这个口子，以增强对泄露出去的电磁波的控制能力。

长线的定义：

当传输线的长度L比其上所传输的电磁波的最小波长$\lambda_{min}$还长，即$L\geq\frac{\lambda_{min}}{100} $时，传输线称为长线，反之则称为短线。（在英文书上这里是$L>>\frac{\lambda_{min}}{100}$,bnh原话：以中文书为准更好，大于等于刚好有个界限）

下图为长线模型：

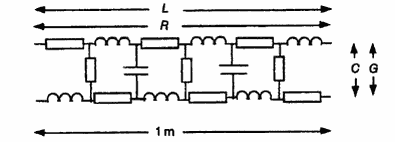
长线的电气特性它的可以用每单位长度串联电阻，串联电感，并联电容，并联电导来描述。一个理想的长线传输线，在线路上的任意一点切入，其电气特性都一样。

传输线的基本特性参数

本小节中的五星级指标: $\gamma$ 和 $Z_0$

理想模型

如果认为是纯纯的理想长线，没有电阻，电感，电容等，那么行波在长线中的传输可以用如下公式描述：

$$v=Vsin\omega t$$

• V：信号振幅
• $\omega$：信号频率

相移常数$\beta$ （phase change coefficient）

如果将电磁波传播速度引入传输线中，电磁波传输造成的延迟，会造成信号的相位变化。因此，引入相移常数$\beta$对此进行建模。

$$v=Vsin(\omega t-\beta x)$$

• $\beta$：相移常数（单位：rad/m）
• $x$​：距离参数（单位：m）

其中$\beta$定义为：

$$\beta=\frac{2\pi}{\lambda}$$

• $\lambda$：波长（单位：m）

物理意义的理解：一个周期的相位变化是$2\pi$，而波长又是波一个周期的长度。因此$2\pi/\lambda$是单位长度上相位变化的程度。

此时，传输线模型如下图所示：

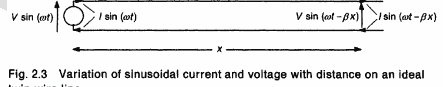
相速度$v_p$ （phase velocity）

对金属线中的行波进行连续“拍照”，会发现它的波峰随着时间在向前移动。这样的波的相位在空间中传递的速度，我们称之为相速度$v_p$。对比一下前面的相移常数，相移常数指的是在固定时刻，随着单位距离移动波的相位变化量。而相速度是指的某一点个相位点，随着单位时间变化相位的变化量。下图中红色点就是相速度。

考虑下图，在$P_1$和$P_2$点相位相同，距离为$Z_1-Z_2$

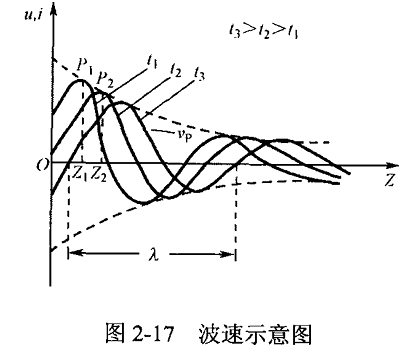
按照相速度的定义来说：

$$v_p=\frac{同相位点移动的距离}{时间差}=\frac{Z_2-Z_1}{t_2-t_1}$$

回顾前面的建模式子：$v=Vsin(\omega t-\beta x)$,某一时刻的相位是由sin括号内的部分来表达的。对于$P_1$点，其相位为$\omega t_1 -\beta Z_1$；同理$P_2$点为$\omega t_2 -\beta Z_2$；

由于$P_1$和$P_2$相位相同，有：$\omega t_1 -\beta Z_1=\omega t_2 -\beta Z_2$，移项改写一下：

$$\omega (t_2-t_1)=\beta(Z_2-Z_1)$$

因此

$$v_p=\frac{Z_2-Z_1}{t_2-t_1}=\frac{\omega}{\beta}$$

因为$\omega =\frac{2\pi}{T}=2\pi f,\beta=\frac{2\pi}{\lambda}$因此$v_p$还可以写成:

$$v_p=\frac{\omega}{\beta}=f\lambda$$

衰减常数$\alpha$

随着距离延长，传输线中衰减是不可不免的。而这种衰减与距离高度相关。因此我们再加上衰减常数$\alpha$(单位：奈培/米)

这个式子需要记住，五星级

$$v=Ve^{-\alpha x}sin(\omega t-\beta x)$$

对于在一条线上相隔单位距离的两个电压幅度的比率，𝑉1和𝑉2有：

$$V_1/V_2=e^{\alpha}$$

这就是信号振幅每单位的衰减程度，衰减系数以 奈培/单位距离 为单位。假设$\alpha=1\ neper/m$，在么每米振幅衰减的比率就是

$$V_1/V_2=e$$

如果将其转化为dB的形式，也就是每米衰减8.686dB

$$20log_{10}(V_1/V_2)=20log_{10}(e)=8.686dB$$

特征阻抗$Z_0$（characteristic impedance）和集肤效应（skin effect）

特征阻抗（Characteristic impedance）是指在传输线（例如电缆、微带线、同轴电缆等）中传播电磁信号时，该传输线上单位长度内的阻抗。

在这样的一节传输线中，特征阻抗的计算公式是：

$$Z_0=\sqrt{\frac{R+j\omega L}{G+j\omega C}}\ (五星级公式)$$

如果是理想传输线，无电阻电导，即R，G=0， $Z_0$此时可写为

$$Z_0=\sqrt{\frac{L}{C}}$$

如果满足特殊条件：$\frac{R}{L}=\frac{G}{C}$，上述式子也成立：

$$Z_0=\sqrt{\frac{L(R/L+j\omega)}{C(G/C+j\omega)}}=\sqrt{\frac{L}{C}}$$

在这个式子中，L和C是独立的，与频率无关。但是R和G会收到频率的影响，这是由于集肤效应（又称趋肤效应）引起的。

Skin Effect（集肤效应）

当导体中有交流电或者交变电磁场时，导体内部的电流分布不均匀，电流集中在导体的“皮肤”部分。也就是说电流集中在导体外表的薄层，越靠近导体表面，电流密度越大，导体内部实际上电流较小，这减少了导体的有效面积，也就增大了电阻。这种现象随着频率的增大愈发明显，这一现象称为趋肤效应(skin effect)。

这是平行双导线不适合高频信号的原因之一。

传输常数$\gamma$

按照前面建立的模型，$v=Ve^{-\alpha x}sin(\omega t-\beta x)$，如果使用一个向量来表示$Vsin(\omega t-\beta x)$中随着距离衰减的部分（即，只和$\beta$相关的部分），那么有：假设向量是$a+jb$

向量的实数就是当前$\beta$造成的电压衰减值，因为在电磁波表示中sin和cos是比较通用的，因为从物理意义上来说，$\beta$在$x=0$处造成相位移动为0，因此用cos来表达。

$$a=Vcos(-\beta x)$$

虚部是波存储起来的电压部分，满足$实数^2 + 虚数^2$=1，因此有

$$b=Vsin(-\beta x)$$

将$a+jb$用欧拉公式表示，有：

$$a+jb=e^{-j\beta x}$$

如果把这个信号自己的电压状态（也就是前面和角频率有关的振幅）记为向量$V_0$，那么传输线上某一点的电压可以表示为

$$V_x=V_0e^{\alpha x}e^{-j\beta x}=V_0 e^{-(\alpha+j\beta)x}$$

其中，这个$\alpha+j\beta$就被称为传输常数，记作$\gamma$，原式可以写成：

$$\gamma=\alpha+j\beta$$ $$V_x=V_0e^{-\gamma x}$$

群速度

相速度是某一个相位点向前移动速度。如果说所有频率的波在同一媒介中传播的相速度都相同，那这没有问题；然而，事实情况是不同频率的波在介质中传播的相速度不同（从相速度的式子就可以看出它和频率有关），因此需要一个物理量来描述其包络的行进速度，也就是群速度。群速度$v_g$是所有的波组合起来的包络的向前移动的速度。在下图中，绿色的点就是群速度。群速度常被认为是能量或信息顺着波动传播的速度。

因不同频率的电磁波在介质中具有不同的相速度而造成电磁信号失真的现象就被称为电磁波色散。

试想一下，有两个正弦波，其各项参数分别为

波1	波2
$\omega$	$\omega +d\omega$
$v_p$	$v_p+dv_p$
$\lambda$	$\lambda+d\lambda$
$\beta$	$\beta+d\beta$

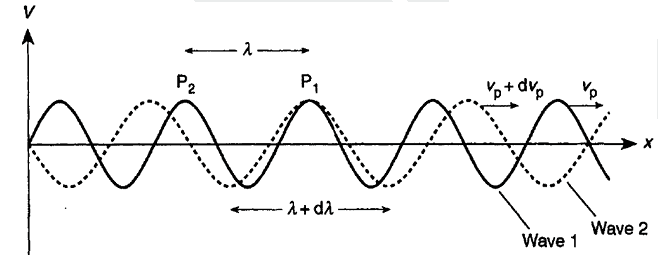
试想一下，现在你站在P1点随着波1移动，波2的尖峰刚好和你重合，你们形成了包络中鼓起来的最高点。同时，在P1的视角下，波2在以$dv_p$的速度向前移动。经过一段时间之后，P1处的尖峰分开，而P2前面的波2尖峰追上了P2，此时P2处形成包络最高点。此时，看起来就像是包络从P1运动到了P2。而经过的这一段时间是：

$$t=\frac{d\lambda}{dv_p}$$

同时，包络的尖峰从P1移动到了P2，刚好移动了波1的波长长度$\lambda$。用包络尖峰移动的距离/移动消耗的时间，就可以得到在P1处观测时，看起来的包络的移动速度。

$$-\lambda\div\frac{d\lambda}{dv_p}=-\lambda\frac{dv_p}{d\lambda}$$

因为在P1处观测的包络的速度+P1向前移动的速度，即可得到群速度

$$v_g=v_p-\lambda\frac{dv_p}{d\lambda}$$

此时便写出了$v_g与v_p$的表达式，但是通常来说，希望回归到波本身，即波的角频率，相移常数等。

分别代入波1和波2的参数：$\lambda = \frac{2\pi}{\beta}, \lambda+d\lambda=\frac{2\pi}{\beta+d\beta}$，相减可以得到

$$d\lambda= \frac{2\pi d\beta}{\beta(\beta+d\beta)}$$

因为$v_p=\frac{\omega}\beta{}, v_p+dv_p=\frac{\omega+d\omega}{\beta+d\beta}$，相减可以得到

$$dv_p=\frac{\beta d\omega-\omega d\beta}{\beta(beta+d\beta)}$$

此时代入$v_g=v_p-\lambda\frac{dv_p}{d\lambda}$:

$$v_g=\frac{\omega}{\beta}-\frac{2\pi}{\beta}\cdot\frac{1}{2\pi}\bigg(\omega -\beta \frac{d\omega}{d\beta}\bigg)$$ $$v_g=\frac{d\omega}{d\beta}$$

因此，最终得到群速度$v_g=\frac{d\omega}{d\beta}$

如果一个脉冲要在不改变其形状的情况下传播，那么与其频谱的不同部分相关的群速度必须相同；换言之，dω/dβ必须与频率无关。如果不是这样，那么脉冲在行进时会改变其形状，通常会在接收器处产生一个随时间分散的波形：这种效应称为色散。

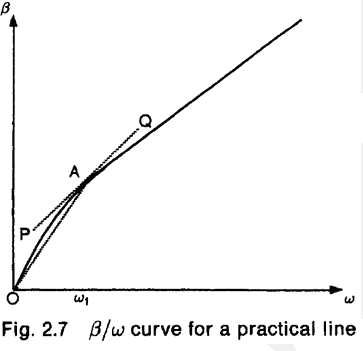
对于发射的无限窄脉冲（即，频域所有频率分量都有的信号），色散量通常表示为接收脉冲在半功率点之间的时间分布。如果绘制β与ω的图（如下图），则该曲线的斜率为dβ/dω，即群速度的倒数。这被称为群延迟（group delay）。如果曲线是一条穿过原点的直线，则相速度和群速度在所有点处都相同且相等。

探究本质：$Z_0,\gamma, \beta $ 和 $\alpha$ 与传输线特性关联

前面提到电压向量用传输常数表达是$V_x=V_0e^{-\gamma x}$，类似地，电流衰减向量也可以表示为$I_x=I_0e^{-\gamma x}$

考虑下图单位长度的传输线，因为基尔霍夫电压定理，环路电压为0。因此有：

$$\delta V=-R\delta xI_x-j\omega L\delta x I_x$$

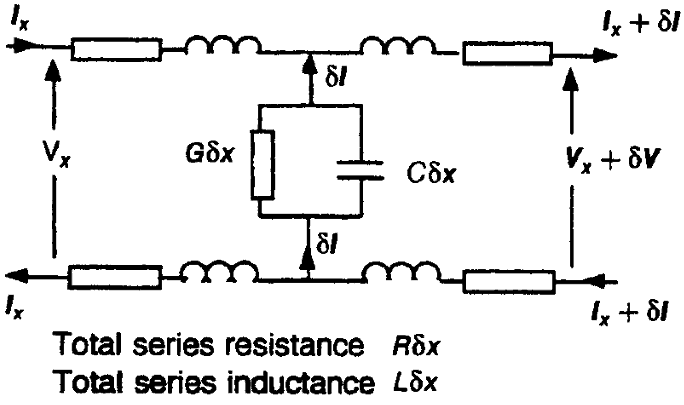
改写一下：

$$\frac{dV}{dx}=-(R+j\omega L)I_x$$

如果忽略上图左侧RL带来的微小压降，则两线间的电流可以表示为$\delta I=-G\delta xV_x -j\omega C\delta xV_x$

$$\frac{dI}{dx}=-(G+j\omega C)V_x$$

如果把$V_x=V_0e^{-\gamma x}$拿来微分一下，有：

$$\frac{dV_x }{dx}=-\gamma V_0e^{-\gamma x}=-\gamma V_x$$

前面$\frac{dV}{dx}=-(R+j\omega L)I_x$的物理意义上单位$x$上电压的变化率，$\frac{dV_x }{dx}$物理意义也是这个，因此，他们两个式子相等，有

$$\gamma V_x=(R+j\omega L)I_x$$

同理，由电压变化率的表达式，可以得到

$$\gamma I_x=(G+j\omega C)V_x$$

上面两式左右分别相除，可以得到

$$\frac{V_x}{I_x}=\frac{R+j\omega L}{G+j\omega C}\cdot\frac{I_x}{V_x}$$ $$\bigg(\frac{V_x}{I_x}\bigg)^2=\frac{R+j\omega L}{G+j\omega C}$$

信号的特征阻抗$Z_0$是电压/电流，因此：

$Z_0$下面两个五星级公式！

$$Z_0=\frac{V_x}{I_x}=\sqrt{\frac{R+j\omega L}{G+j\omega C}}$$

如果对于理想的没有电阻$R$和电导$G$的导线，或者是$\frac{R}{L}=\frac{G}{C}$的导线，有：

$$Z_0=\sqrt{\frac{L}{C}}$$

$\frac{R}{L}=\frac{G}{C}$被称为无失真条件，但实际永远不会接近它，即 G/C 比 R/L 小得多。过去，一些传输长距离信号的线路加电感器，以使R/L比更接近G/C，但这种做法现在已经过时了。

传输常数$\gamma$也可以与传输线特征关联：

前面得到的$\gamma V_x=(R+j\omega L)I_x$和$\gamma I_x=(G+j\omega C)V_x$两侧各有一个$I_x$和$V_x$，那么，将这两个式子相乘就可以约掉它们，只保留$\gamma$

$$\gamma^2V_xI_x=(R+j\omega L)(G+j\omega)I_xV_x$$

下面这个$\gamma$五星级公式！

$$\gamma=\sqrt{(R+j\omega L)(G+j\omega C)}$$

1、在理想传输线的前提下，即，R=G=0时

$$\gamma=j\omega \sqrt{LC}$$

有了$\gamma$之后，可以进一步推得$\beta,v_p,v_g$,

在理想传输线的前提下，即，R=G=0时，$\gamma$为纯虚数，因此$\gamma$全部由$\beta$贡献

$$\beta = \omega\sqrt{LC}$$ $$v_p=\omega/\beta =\frac{1}{\sqrt{LC}}$$ $$v_g=\frac{d\omega}{d\beta}=\frac{1}{\sqrt{LC}}$$

2、在无失真条件(distortionless condition)，即$R/L=G/C$时

$$\gamma=\sqrt{LC(R/L+j\omega)(G/C+j\omega)}=(R/L+j\omega)\sqrt{LC}$$

因为$\gamma=\alpha+j\beta$，拆分上式虚部和实部，可以得到$\alpha$和$\beta$的式子（$\beta$和理想状态相同)：

$$\alpha=\frac{1}{2}\bigg[R\sqrt{C/L}+G\sqrt{L/C}\bigg]$$

继续推导，将$\gamma$写回$\gamma^2$:

$$\gamma^2=(\alpha+j\beta)^2=(R+j\omega L)(G+j\omega C)$$ $$\alpha^2-\beta^2+j2\alpha\beta=RG-\omega^2LC+j\omega(LG+RC)$$

拆分虚实部，可以得到：

$$\alpha ^ {2} - \beta ^ {2} =RG- \omega ^ {2} LC$$ $$2 \alpha 8= \omega (LG+RC)$$

联立求解上述二式

$$\alpha =\{ \frac {1}{2} [ (R^ {2}+\omega ^ {2}L^ {2})^ {1/2} (G^ {2}+\omega ^ {2}C^ {2})^ {1/2} +(RG- \omega ^ {2} LC)]\}^{1/2}$$ $$\beta =\{ \frac {1}{2} [ (R^ {2}+\omega ^ {2}L^ {2})^ {1/2} (G^ {2}+\omega ^ {2}C^ {2})^ {1/2} -(RG- \omega ^ {2} LC)]\}^{1/2}$$ $$\gamma=\alpha+j\beta=\sqrt{RG+j\omega CR+j\omega GL-\omega^2LC}$$

在高频情况下，RG可以忽略，提出$(-\omega^2LC)$，上式可以写为

$$\gamma=j\omega\sqrt{LC}(1-j\frac{CR+GL}{\omega LC})^{\frac{1}{2}}$$

因为这是高频情况，$\omega$很大，以此可以约等于：

$$\gamma\approx j\omega \sqrt{LC}\bigg(1-\frac{1}{2}j\frac{CR+GL}{\omega LC}\bigg)$$

乘进去，并拆分虚实部，最终可以得到：

下面$\gamma,\alpha,\beta$五星级公式！

$$\gamma \approx \frac {1}{2} \frac {CR+GL}{\sqrt {LC}} + j\omega \sqrt {LC}$$ $$\alpha =( \frac {R}{2} \sqrt {\frac {C}{L}} + \frac {G}{2} \sqrt {\frac {L}{C}} )(Np/km)$$ $$\beta =j \omega \sqrt {LC} (rad/km)$$

传输线特性参数公式总结

相移常数

• 定义式：$\beta=\frac{2\pi}{\lambda}$
• 理想传输线，R=G=0时：$\beta = \omega\sqrt{LC}$
• 无无失真传输线，$R/L=G/C$，且高频下：$\beta =j \omega \sqrt {LC}(rad/km)$

传输常数

• 定义式：$\gamma=\alpha+j\beta$
• 与传输线特征关联：$\gamma=\sqrt{(R+j\omega L)(G+j\omega C)}$
• 理想传输线，R=G=0时：$\gamma=j\beta=j\omega\sqrt{LC}$
• 无失真传输线，$R/L=G/C$，且高频下：$\gamma \approx \frac {1}{2} \frac {CR+GL}{\sqrt {LC}} +
  j\omega \sqrt {LC}$

特征阻抗$Z_0$

• 定义式：$Z_0=\frac{V_x}{I_x}=\sqrt{\frac{R+j\omega L}{G+j\omega C}}$
• 无失真传输线或理想传输线下：$Z_0=\sqrt{\frac{L}{C}}$

衰减常数

• 定义式：间隔单位距离的$V_1$和$V_2$, $V_1/V_2=e^{\alpha}$
• 无失真传输线，$R/L=G/C$，且高频下：$\alpha =( \frac {R}{2} \sqrt {\frac {C}{L}} + \frac {G}{2} \sqrt {\frac {L}{C}} )(Np/km)$
• 理想传输线，R=G=0时：无衰减，$\alpha=0$

相速度

• 定义式：$v_p=\frac{\omega}{\beta}=f\lambda$
• 理想传输线下：$v_p=\omega/\beta =\frac{1}{\sqrt{LC}}$

群速度

• 定义式：$v_g=\frac{d\omega}{d\beta}$
• 理想传输线下：$v_g=\frac{d\omega}{d\beta}=\frac{1}{\sqrt{LC}}$

传输线的反射

BNH补充小课堂：由于接收器端无法完全消耗信号的能量，因此波会发生反射。同频反射的信号会对正向传输的信号进行干扰。因此需要进行阻抗匹配，同时，在部分短距离传输系统上还需要在接收端前加衰减器。

两个极端-接收端开路/短路

传输线在末端可以理想考虑为短路和开路两种情况，也就是负载阻抗无穷和负载阻抗为0时。

• 负载阻抗无穷时，反射系数为1，波正相反射，并与正向传播的波叠加幅值变为2倍。

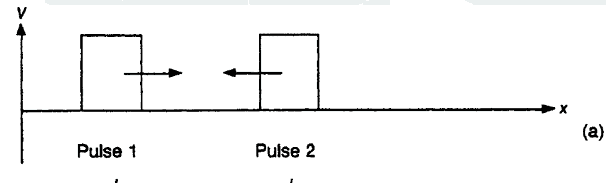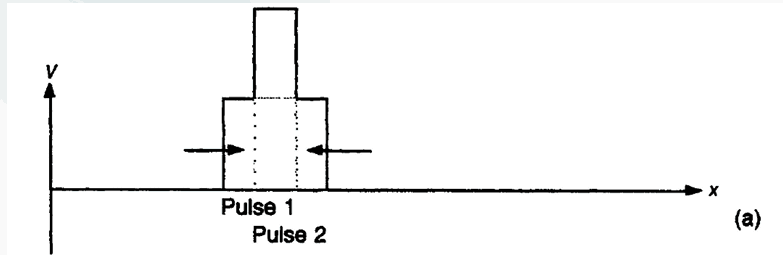• 负载阻抗为0时，反射系数为-1，波反相反射，消除正向传播波的幅值

• 负载阻抗与传输线特征阻抗匹配时，无反射发生。此时称阻抗正确匹配(correctly terminated or matched)。

如果负载端阻抗大于特性阻抗但不等于无穷，则以开路去分析，幅值会叠加，但是小于2倍。

若负载端阻抗小于特性阻抗但不为0，则带入短路去分析，幅值会相消，但是不完全消除。

对反射波进行建模

若将前进波的电压电流表示为$V_i,I_i$，反射波的电压表示为$V_r,I_r$。

那么总电压是：$V_i+V_r$, 总电流是$I_i-I_r$。参考下图，此时$R_L$上的电压就是总电压，电流就是总电流，因此：

$$\frac{V_i+V_r}{I_i-I_r}=R_L$$

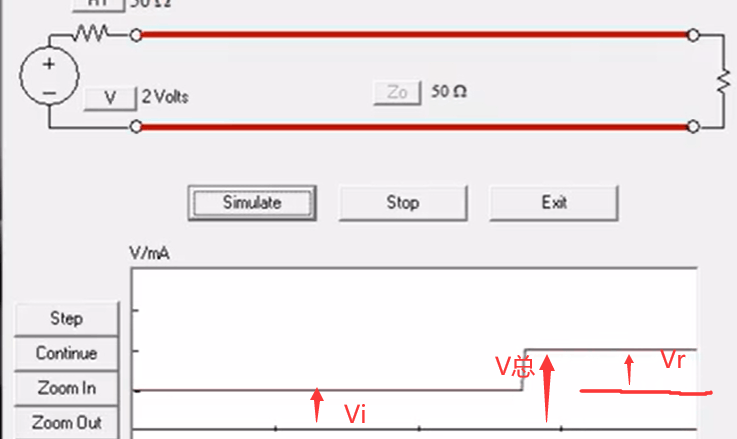
其中，$V_r/V_i$被称为电压反射系数（voltage reflection coefficient），记为$\rho$。对于理想传输线，其呈纯阻性，因此电阻恒定，电流比值也为$\rho$。（这个地方如果是考虑单一频率，即，阻抗不变的情况，则无需理想传输线）

$$\rho=\frac{V_r}{V_i}=\frac{I_r}{I_i}$$

如果以传输线的视角来看，传输线呈现的纯阻性为$R_0$，有：

$$\frac{V_i}{I_i}=\frac{V_r}{I_r}=R_0$$

如果对$R_L$除以$V_i/I_i$,再在前面乘回去，可以推得其用$\rho$表示：

$$R_L=\frac{V_i}{I_i}\cdot\frac{1+V_r/V_i}{1-I_r/I_i}=R_0\cdot\frac{1+\rho}{1-\rho}$$

换过来，便可以求得$\rho$与$R_0,R_L$的关系：

$$\rho=\frac{R_L-R_0}{R_L+R_0}$$

举个例子，如果$R_L=\frac{1}{2}R_0$,则 $\rho=-1/3$，意为反射电压相位相反，振幅为$1/3V_i$

如果不是理想传输线，考虑单一频率的情况下，线阻恒定为$Z_0$，负载阻抗恒定为$Z_L$，$\rho$也可以表示为。在这种情况下，$V_i,V_r,I_i,I_r$是一个向量（或者复数），因为其表示的含义是波。

$$\rho=\frac{Z_L-Z_0}{Z_L+Z_0}$$

回波损耗(Return loss)

反射脉冲中的能量与入射脉冲中的能量之比称为回波损耗，由于同一线缆上电流恒定，因此可以直接由电压的比例的平方$\rho^2$得到

$$Return\ loss=10log_{10}(\rho^2)=20\log_{10}(\rho)$$

全驻波（total standing wave）

在下面的推导中，都以无衰减的理想传输线，衰减常数$\alpha=0$

假设传输线的长度为$x$，$Z_L=\infty$。此时电压会完全同相位反射。如下图所示。

如果在起始点P的电压为V，那么经过$x$的距离，终点的电压$V’$就是：

$$V'=Ve^{-j\beta x}$$

此时这个电压会被同相位完全反射，那以终点至起始点的反射波的视角来看，反射回起始点的电压是：

$$V''=V'e^{-j\beta x}$$

将$V’=Ve^{-j\beta x}$改写为$V=V’e^{j\beta x}$。起始点的电压是正向传播电压和反射电压的和，因此：

$$V_p=V+V''=V'e^{j\beta x}+V'e^{-j\beta x}=V'(e^{j\beta x}+e^{-j\beta x})$$

使用欧拉公式展开：

$$V_p=2V'cos(2\beta x)$$

有相移常数定义式$\beta=2\pi/\lambda$，记$2V’=V_T$有：

$$V_p=V_Tcos(2\pi x/ \lambda)$$

不妨想一下，这个$V_p$可能并非是真正的信号发生点，而是人为规定的一个“起点”。也就相当于，这个式子可以是线路上任意一点的电压值，而$x$代表的是这一点距离终点的长度。观察发现：

• 当线缆距离终点满足$2\pi x/\lambda=k\frac{\pi}{2}$ (k=1,3,5,7…)，即$4x/\lambda=k(odd), x=\frac{k\lambda}{4}$，时，电压为0；
• 当线缆距离终点满足$2\pi x/\lambda=k\frac{\pi}{2} (k=0,2,4,6…)$时，即$4x/\lambda=k(even),x=\frac{k\lambda}{4}$时，电压为$V_T$或$-V_T$；

因此，在线缆上每隔$\lambda/4$的距离，形成一个波节(nodes)；每隔$\lambda/4$的距离，形成一个波峰（antinodes）

行驻波（partial standing wave）

假设存在衰减，并非全部能量反射。那么波形可以被看成是一部分的正向行波和反射波对冲，形成全驻波，另一部分仍然是正向行波。传输线上的波形是这二者波形的叠加。在传输线上，电压最大值是行波电压和反射电压幅度的总和，最小值是它们的差值（不再为零）。此时传输线上最大电压和最小电压的比值被称为“电压驻波比voltage standing wave ratio (VSWR)”，记为S

$$V_{max}=V_i+V_r, V_{min}=V_i-V_r$$ $$S=\frac{V_{max}}{V_{min}}=\frac{V_i+V_r}{V_i-V_r}$$

对S分子分母同除以$V_i$，再结合前面的反射系数$\rho$:（考虑$\rho$是有正负的，但是$S$一定是最大的比最小的，因此$\rho$需要加绝对值）

下面VSWR公式和其逆公式五星级

$$S=\frac{1+\frac{V_r}{V_i}}{1-\frac{V_r}{V_i}}=\frac{1+|\rho|}{1-|\rho|}$$

反过来也可以由$S$得出$|\rho|$

$$|\rho|=\frac{S-1}{S+1}$$