多路复用器

多路复用器可以使用逻辑门制造，也可以使用Transition Gate 制造。一个多路复用器具有n个输入，那么就需要$log_{2}{n}$路选择信号。考试中最多出现4 to 1多路复用器。

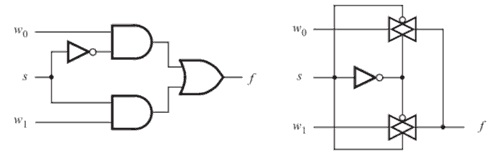
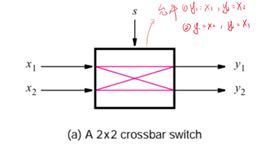
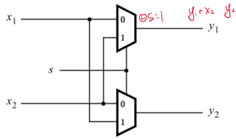
例题：2x2交叉选择器

使用多路复用器构建逻辑函数五星级中的五星级

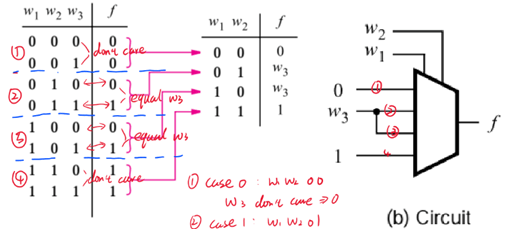
如上图这个情况，使用$w_1,w_2$做为选择信号，可以把输出分为4个case：

Case 0: $w_1=0,w_2=0$, 输出为0
Case 1: $w_1=0,w_2=1$, 输出等于$w_3$
Case 3: $w_1=1,w_2=0$,输出等于$w_3$
Case 4: $w_1=1,w_2=1$,输出等于1

这样就实现了用多路复用器来实现基础的逻辑组合。除了简单的电路外，还可以使用逻辑门的输出和多路复用器进行组合，实现更复杂的电路。

香农拓展定理（Shannon’s Expansion Theorem）

香农拓展定理的核心理念是：对于一个Boolean function, 可以把它写为分解为$w_1 (…)+ \overline w_1 (…)$，也就是$w_1$和$\overline w_1$下的两种情况。这里的$w_1$为称为辅因子(cofactor). 那么对于一个有$w_n$项的布尔函数，把$w_1$作为辅因子，可以写成如下表达式：

$f( w_ {1} , w_ {2} , \cdots , w_ {n} )= \overline {w}_ {1} \cdot f(0, w_ {2} , \cdots , w_ {n} )+ w_ {1} \cdot f(1, w_ {2} , \cdots , w_ {n} )$

几个分解的例题：

例1：

$f( w_ {1} , w_ {2} , w_ {3} )= w_ {1} w_ {2} + w_ {1} w_ {3} + w_ {2} w_ {3}$

可分解为：

$f= w_ {1} w_ {2} + w_ {1} w_ {3} +( w_ {1} + \overline {w_ {1}} ) w_ {2} w_ {3} = w_ {1} ( w_ {2} + w_ {3} + w_ {2} w_ {3} )+ \overline {w_ {1}} ( w_ {2} w_ {3} )= w_ {1} ( w_ {2} + w_ {3} )+ \overline {w_ {1}} ( w_ {2} w_ {3} )$

例2

$f= w_ {1} \oplus w_ {2} \oplus w_ {3}$

可分解为：

$f=\overline w_1(w_ {2} \oplus w_ {3} )+ w_ {1} ( w_ {2} \oplus w_ {3} )$

例3

$f= \overline {w}_ {1} \overline {w}_ {3} + w_ {1} w_ {2} + w_ {1} w_ {3}$

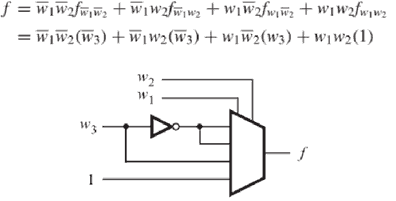
使用$w_1$作cofactor：

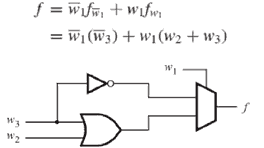
使用$w_1w_2$做cofactor：

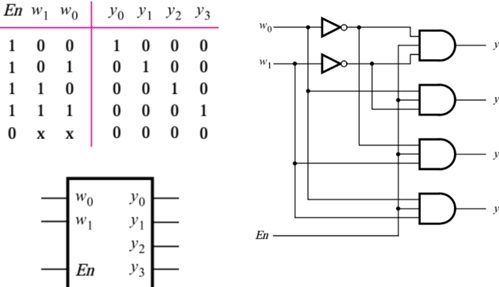
解码器（decoders）

解码器电路接受$n$个输入，产生$2^n$个输出。其作用是将收到的数据映射到对应的线路上去。举个例子，假设一个2bit decoder受到的数据是11，对应十进制是3（第四个数，从0开始数），那么它会把输出的第4条线置高电平。下面是一个2bit解码器的例子

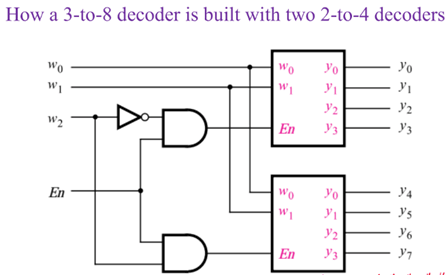
使用多路复用器的思路，也可以用两个2 to 4 decoder 合成一个 3 to 8 decoder

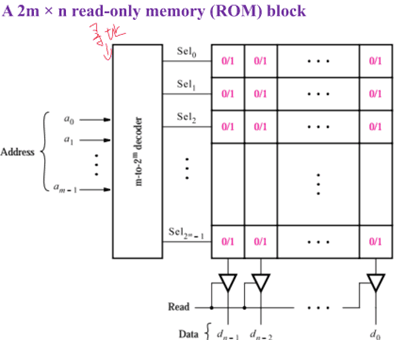
解码器最重要的应用之一是用于存储信息的存储块寻址：

输入想要访问的存储单元的地址，解码器即可将那一行使能（此处可以b站了解一下NAND闪存或者固态硬盘工作原理）

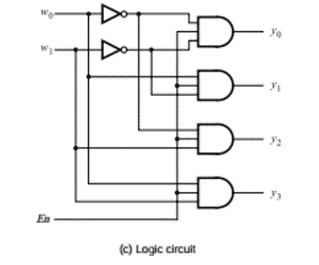
多路分解器（Demultiplexer）

Multiplexer使用不同switch输入组合选择输出不同的单条线路。Demultiplexer使用不同的Switch输入组合将单条线路输出到在多个不同的数据输出上。

Demultiplexer 可以用 Decoder实现，下图就是个例子。右图$w_1 w_2$被用作Switch 信号，En被用作输入信号。$w_1 w_2$控制En信号在那条路上被输出。

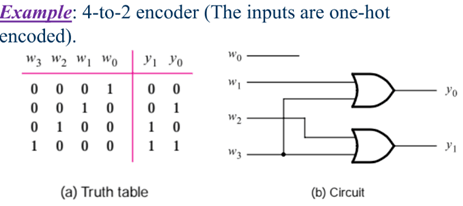
编码器（Encoder）

编码器是Decoder的逆过程，它接受$2^n$条输入，产生n个输出。n个输出呈现二进制数，用于表示是哪一条输入。

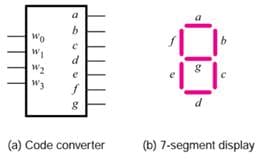
译码器（Code Converter）

把输入翻译成特定的输出。例如用来点亮7为数码管的code converter, 会把二进制数字输入转化成对应的pattern输出。

算术比较电路

算术比较电路接受两个二进制数输入，记为A和B，比较A和B大小后输出A>B,A=B,A<B三个输出。

举个例子：

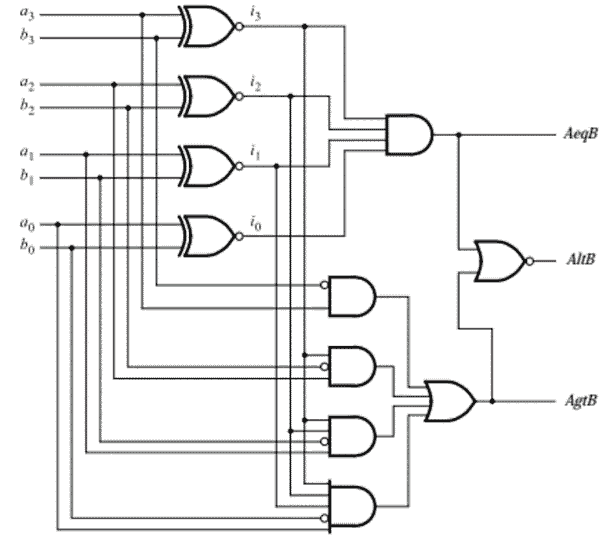
在这个例子中，定义一个中间信号$i_k=\overline {a_k\oplus b_k}$

则：A=B可表示为：$AeqB=i_3i_2i_1i_0$，A>B可表示为$AgtB= a_ {3} \overline {b}_ {3} + i_ {3} a_ {2} \overline {b}_ {2} + i_ {3} i_ {2} a_ {1} \overline {b}_ {1} + i_ {3} i_ {2} i_ {1} a_ {0} \overline {b}_ {0}$ ， A<B可表示为：$AltB=\overline {AeqB+AgtB}$

算术比较电路也可被分为两类：有符号的，无符号的。

有符号的：认为输入的数据是以补码的形式输入的，第一位为符号位，这类算术比较电路通常使用加法电路来比较大小
无符号的：认为输入数据都是原码格式，没有符号位，这类算术比较电路通常直接比较，上图就是无符号的例子