智能系统设计-Part2.2-图像压缩
引入
图像的冗余信息
编码冗余(encoding redundancy):下图这个图像中,只有4种颜色,如果采用8bit色深编码,则会有252种值从未被使用。
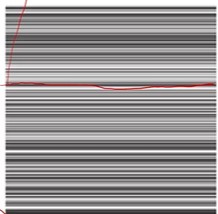
空间冗余(spatial redundancy):下图每一行都是一样的像素点,如果每一个像素都独立记录值,则会浪费很多空间。如果能记录256个像素的一条线,再记录这条线重复256次,那么将会剩下很多的空间。
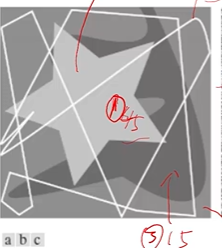
无关信息(irrelevant information):下图的灰度值差异很小很小,肉眼不可查(下图左)。除非使用直方图均衡等算法(下图右),否则图像信息不可见。因此其为可压缩信息。

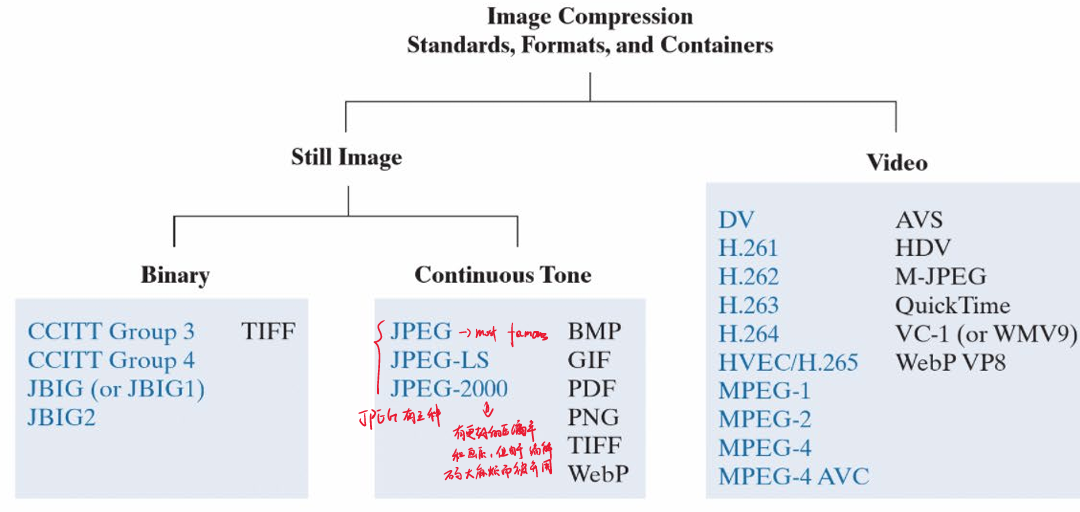
主流音视频压缩格式
图像编码的总体流程
图像存储在设备上,可以总地分为如下几个步骤:
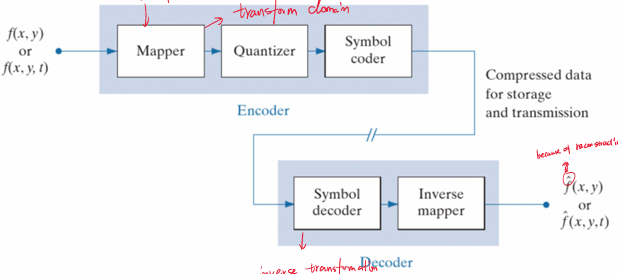
映射器(Mapper):将原图像的$f(x,…)$变换为减少空间和时间冗余的格式,这一操作是可逆的,但并不会减少数据量。在后续介绍JPEG压缩时会介绍DCT变换。
量化器(Quantizer):上一步中,mapper将图像转化到变换域,量化就是将变换域中的数根据存储的比特要求量化成特定值。这一过程会损失信息,如果是无损压缩,则需要舍弃这一步。
符号编码器(Symbol coder):根据图像变换域的特性,可能会出现一些特殊的数据规则,例如内含很多个0。此时对这些数据采用特殊的编码方式,即可无损地节省很多存储空间。例如后面介绍的霍夫曼编码。
JPEG图像压缩过程
引入
JPEG图像是有损压缩,其利用了人眼的两个性质:对色彩不如对明度信息敏感;对细节(高频变换的图像)不敏感。
色彩敏感性
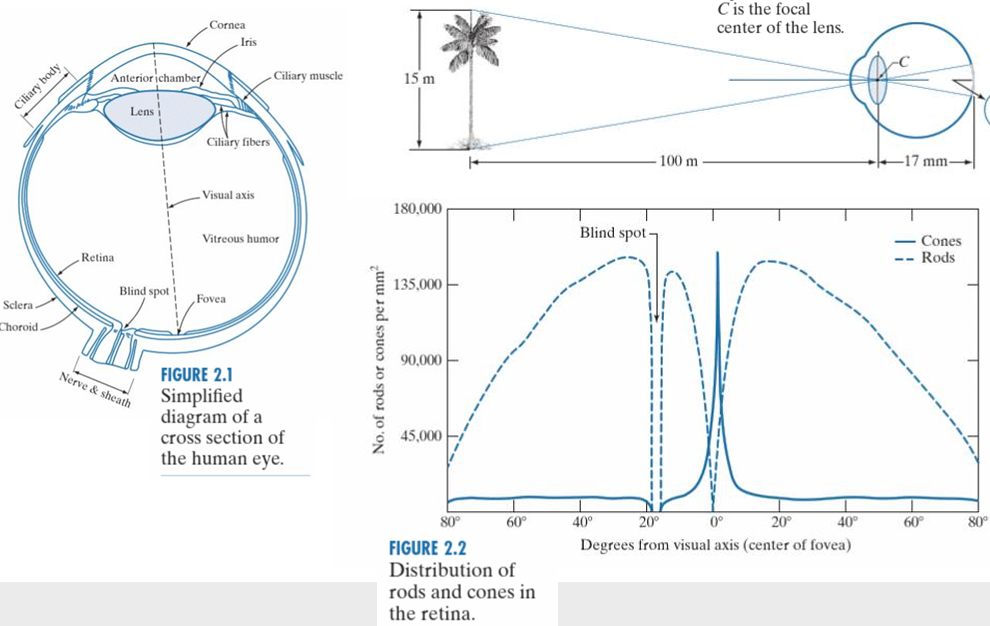
回顾前面的人眼视觉系统,人眼内有视椎细胞和视杆细胞,而根据上图的细胞分布情况,视椎细胞比视杆细胞少的多。由于视椎细胞对颜色敏感,视杆细胞对明度敏感,因此人类对颜色的察觉能力比对敏感信息的察觉能力小得多。
利用这个特性,JPEG规定RGB色彩不再使用三个RGB图层,而是分为明度(Luminance)蓝色和红色偏移量成分三个图层。这一步是独立于之前介绍的步骤之外的,这些知识与本节课内容无关,只是介绍。

在这三个图层的基础上,规定明度图层全采样,剩下两个图层间隔采样。即可实现初次压缩。初次压缩后,就需要将三个图层逐次放入映射器、量化器、符号编码器。
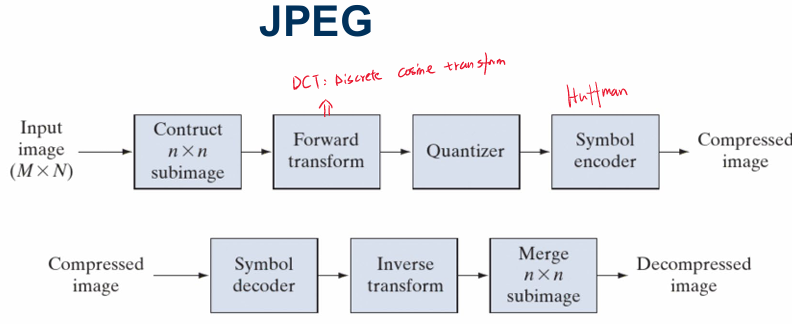
值得一提的是,在映射器进行变换之前,图像是被切割成$n\times n$的小图进行处理的(通常是8x8)。这是由于它是用的变换(DCT算法)的特性决定的。后续将详细介绍。
DCT
JPEG的映射器使用离散余弦变换(Discrete Cosine Transform,DCT)。
对于MxN大小的图像变换而言,其通式可以写为:
正变换:
逆变换:
其中$f(x,y)$为图像某一点的像素信息,$r(x,y,u,v)$和$s(x,y,u,v)$为变换矩阵。除了DCT之外,还有一种变换算法交KLT(Kahunen-Loeve Transform),KLT变换损失的信息很少,但是有这些缺点:变换矩阵与图像有关,因此不同图像就需要计算不同的变换矩阵
但是DCT的变换矩阵却是定值,而且逆变换和正变换的变换矩阵一样。因此虽然DCT会造成更多信息损失,但是JPEG还是采用DCT。
图像的频率
为了更好理解现在我们只考虑明度图层,且将8x8的图像简化为一个1x8的图像,按照图像的灰度值将这一行像素绘制在坐标轴上,即可得到这样的一个“信号”
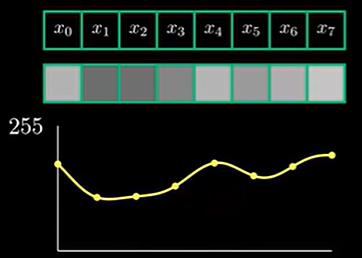
从这里可以看出,如果明暗交替越快,信号频率就越高。我们学过离散傅里叶变换,知道任何信号都可以使用正余弦叠加来还原,那么有没有可能能用各种余弦信号拟合出这个信号呢?是可以的,这就是DCT在干的事情。和DFT一样,在DCT中,变换后的$X_0$位置存放直流信号强度,$X_7$位置存放最高频信号强度,如下图所示。
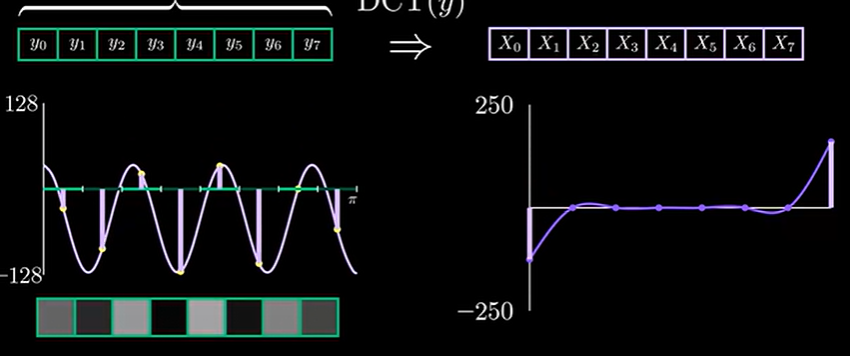
这一部分可以参看离散余弦变换可视化讲解_哔哩哔哩_bilibili,非常清晰。
DCT原始图像
如果现在恢复到8x8的图像呢?那么除了横向频率之外,还有一个纵向频率。他们组合起来就得到了DCT变换域图像:
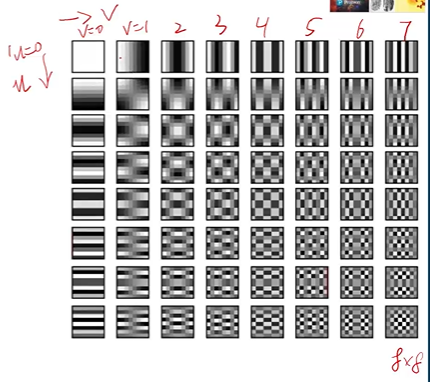
从上图可以看到,左上角为直流,右下角为横向、纵向频率都最高的点。
从定义式到原始图像
DCT的变换式子为:
其中$\alpha$为归一化函数,定义为:
不妨带入u和v计算一下值,发现当u,v均等于0时,这是一个没有频率的直流分量。而增大u或者v,带有参数x或y的cos频率也会相应地增加。这就得到了是DCT原始图像。这也就是为什么下图横轴与v的值有关,纵轴与u的值有关。

DCT式子变换的结果,就是用上面这个8x8图像去拟合输入8x8图像的参数,类似于傅里叶变换。DCT变换得到的就是DCT原始图像的强度,类似于傅里叶变换中每个频率分量的强度。原有的图像矩阵就可以变成这样一个矩阵:
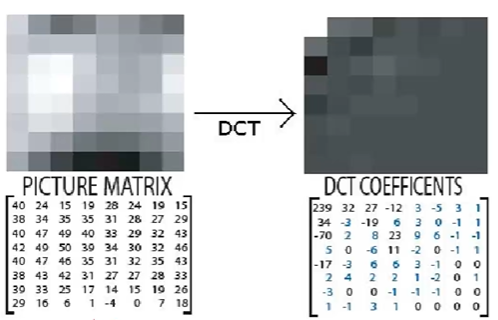
观察上面的矩阵,可以看到左上角数值偏大,而右下角数值偏低,换句话说,也就是低频信号多,高频信号低。回顾前面,我们提到选择8x8的子图像挨个变换,就是因为在8x8的图像内,像素信息不会发生太大的变化,可以确保低频信息占主导。下图是DCT后,直接逆变换回来的RMSE与其他变换算法的对比。
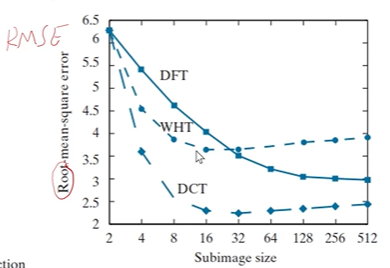
在前面提到,人眼对细节(即高频变换的图像)不敏感,因此在这个地方如果舍弃部分高频信息,人眼也不会察觉。至此就要进入下一步量化。
量化
几种裁切遮罩
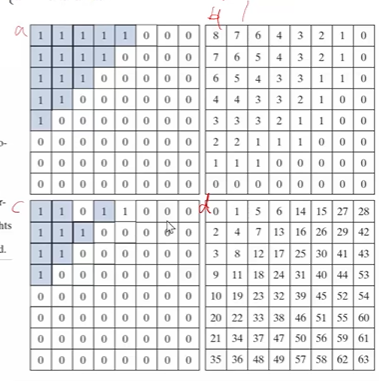
JPEG在进行量化时,会使用遮罩矩阵(mask)对DCT得到的结果进行裁切,以在量化部分剔除部分不敏感的信息(以高频分量为主)。下图的a、b、c展示了三种裁切矩阵。
a. 分区裁切(zonal mask):保留左上角一定区域的低频信息,将右下方的高频信息剔除。
b. 分区比特分配(zonal bit allocation):左上角低频信息用8个bit存储,越往高频比特数量越低,指导最高频不使用bit存储。
c. 阈值裁切(threshold mask):如果某一频率信号超过某种强度,则将其保留,若小于则使其乘以0消除。
量化过程实现
在上面介绍的几种裁切方式中,可以发现都有效地隐去了高频分量。但是在如何在量化过程中实现裁切呢?这里给出一种使用量化表实现的例子
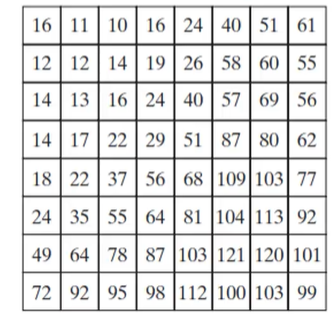
首先定义一个量化表(normalization matrix/ quatization table),如下图所示。各频率信号有不同的参数,低频信号参数偏小,高频信号参数偏大。下表的数值与JPEG的质量参数有关,质量越低,量化步长就越大,量化表是由JPEG标准给出的。
在量化时,使用下式:
其中round表示四舍五入,T是变换后的原始强度值,Z是上述量化表。
举个例子,假设有一个图像变换后直流强度$T(0,0)=161$。那么按照上述量化表:
下面给出了一个真实图像经过JPEG标准量化表后得到的结果,可以看到高频几乎全为0。

接下来就需要把这个矩阵存储起来。我们希望把0连续地放在一起,这样在数据结尾直接放有多少个0的标识以节省空间。因此规定量化后数组的存储顺序为下图这样的蛇形
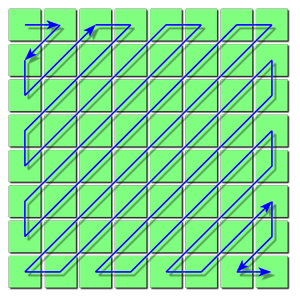
因此最后得到的数组就是:-26,-3,0,-3,-2,-6,2,-4,1,-3,0,1,5,,1,2,-1,1,-1,2,0,0,0,0,0,-1,-1,EOB
其中EOB表示这个之后全是0了。这个数组里面的一堆0可以通过霍夫曼编码有效地再次无损压缩
霍夫曼编码
霍夫曼编码是一种可变长编码(variable length)。它压缩数据的理念是将出现次数多的值用短长度的编码表示,出现次数少的值用长长度的编码表示。例如上面JPEG压缩后0很多,那么0就可以用单个bit的0或者1表示。例如245这个值出现次数很少,那就用诸如10011110101等等的一长串编码表示。这样就可以巧妙地减少存储空间。
霍夫曼树
霍夫曼编码可以由霍夫曼树写出来,这里会给一个详细的例子。
假设有6个值,值分别为$a_1,a_2…a_6$,其对应的出现概率如下表
| a1 | a2 | a3 | a4 | a5 | a6 |
|---|---|---|---|---|---|
| 0.1 | 0.4 | 0.06 | 0.1 | 0.04 | 0.3 |
Step1:选出出现概率最小的两个,按照左大右小放置,将他们的概率加起来作为父节点
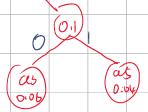
Step2.1:将概率1的父节点概率放回原来的数组,再次挑出概率最低的两个,此时Step1 父节点、a1、a4都是0.1可以随意选2个。这里以选择Step1 父节点和a4为例。父节点和a4还是按照左高右低放置,因为这里是等于,因此可以随意左右。
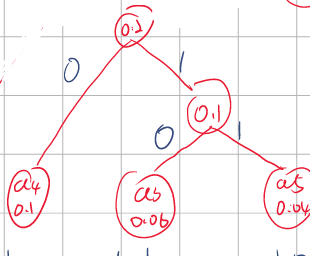
Step2.2:将这两个组合的父节点0.2再次放回,重复上一个步骤,会选出a1=0.1和父节点=0.2。还是按照左高右低放置,父节点和它的叶在左边。
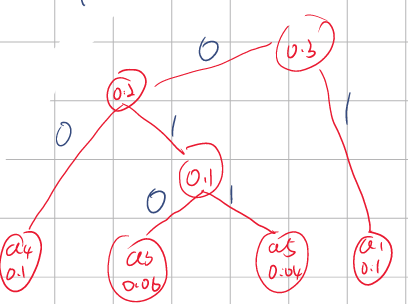
Step2.X:重复这个步骤,直到列表被选完。就可以得到霍夫曼树
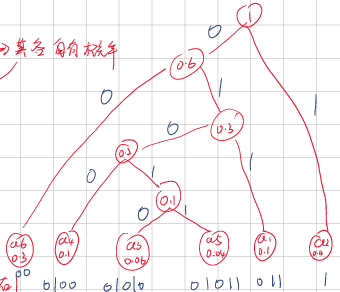
Step3:如上图,将每个父节点的左边标记0,右边标记为1;或者左边标记为1,右边标记为0。由父节点到最后的元素挨个顺下去,从左到右挨个记录01,就是该元素的霍夫曼编码值。
例如a1这个元素,首先从最大父节点顺下来:
1 这里靠左是0;
0.6这里靠右,是1;
0.3这里靠右,是1;
因此a1的霍夫曼编码值就是011。
另一种写法的霍夫曼树
下图是另一种写法的霍夫曼树:
- 先将各个元素按照概率排列。然后将末尾2个最小概率相加得到下一列,重复这个步骤直到只剩2个概率。
- 然后按照靠上分配0靠上分配1(下图例子靠上分配0),挨个把加起来的概率进行展开。
- 当展开时,展开出的2个概率的编码前缀和其父节点(即被展开的概率)一致,并在其末尾再次分配上0下1。