本篇文章涉及通信原理知识，需要掌握一定通信原理基础，了解基带调制，频带调制，相干解调，码元(符号)传输速率，Power Spectrum Density 等

有三种基本的扩频方式：

跳频扩频(Frequency-hopping speread spectrum)
直接序列扩频(Direct-sequence spread spectrum)
啁啾扩频/线性调频扩频(Chirp Spread Spectrum)

跳频技术(FHSS)

传统的无线通信系统，发射机和接收机工作在单次通信过程中，载频一般是保持不变；例如通信频率是900MHz, 那么通信将一直使用这个频率进行。

跳频（Frequency Hopping)系统则在单次通信中，载频在多个频率上跳变。如901MHz, 902MHz etc.

跳频系统的调制与解调

跳频的调制发生在频带调制之前。如下图所示，原始数据D(t)经过信息调制器后变成基带信号；同时产生一个伪随机序列来控制载波信号按照一定的规律跳变。接收端需要使用产生本振信号(local oscillator)进行相干，产生一个中频信号，中频信号再进行检波/解调。

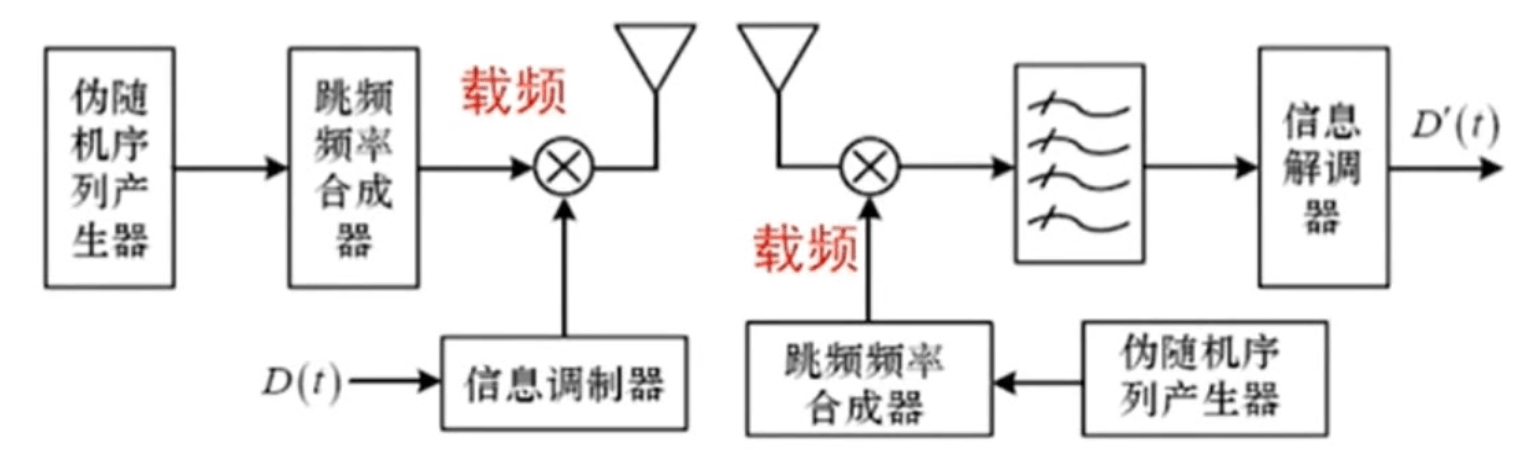
伪随机序列控制下的载波频率如下图所示，在不同频段间跳跃，这个图被称为跳频图案，通信双方可根据实时参数及密钥推算得到当前跳频图案

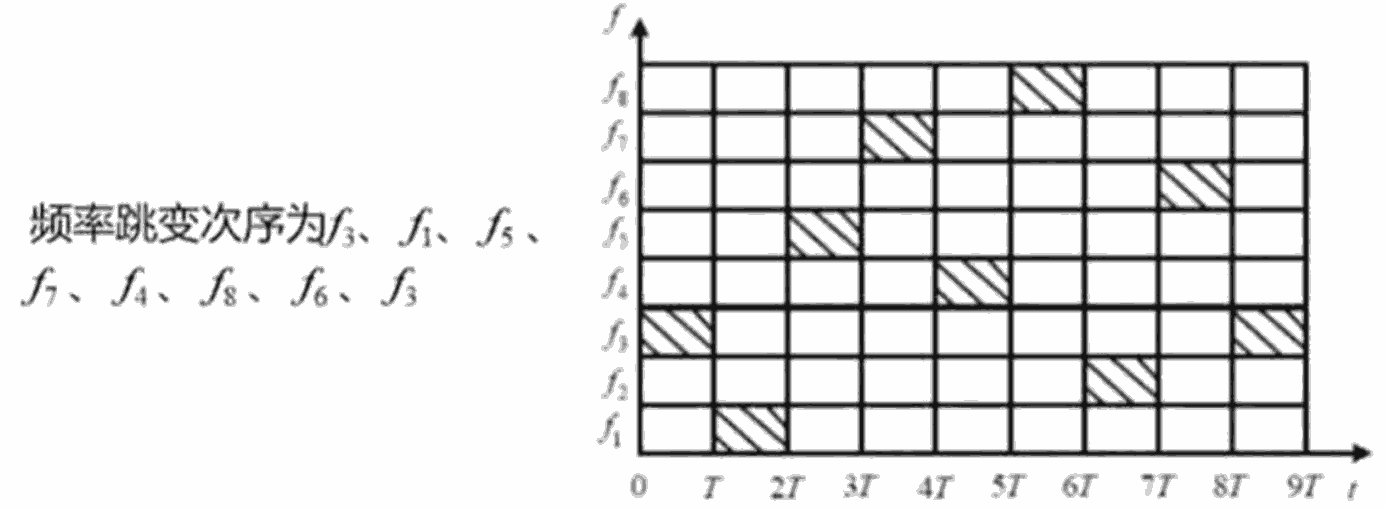
对于产生跳频，有如下要求：

(同一跳频图案具有良好的自相关性(类似冲激函数)
不同跳频图案具有良好的互相关性(相关值趋近于0
跳频图案具有良好的随机性，足够大的线性复杂度(抗截获和抗破译)
周期长和图案多(减小系统中各用户间的频点碰撞概率

跳频可以分为快跳频和慢跳频：

快跳频：跳频周期小于符号周期(是Ts的约数)，一个符号传输需要多个频率
慢跳频：跳频周期大于符号周期(是Ts的倍数)，一个频率传输多个符号

跳频通信可以带来很强的抗干扰能力的原因：

在同一时刻，干扰信号频率只有与跳频信号所在频率相同，且干扰信号能量足够大时，才能造成严重的影响
由于跳频图案具有伪随机性，其周期可长达数十年甚至更长，跳变的频率可达成千上万个，因此可以有效地躲避干扰。因此除非破译跳频图案，否则仅在某一频率或某几个频率上长时间施放干扰是无济于事的。而在整个频段长时间施放干扰难度很大

多址通信

多址技术是指把处于不同地点的多个用户接入一个公共传输媒质，实现各用户之间通信的技术。

例如，常见的多址技术有频分多址（FDMA）、时分多址（TDMA）、码分多址（CDMA）。

FDMA：不同用户使用不同的频率
TDMA：不同用户发送时刻不同，以不同时隙实现通信
CDMA：以不同的代码序列来实现通信，码分多址的基本思想是靠不同的地址码来区分的地址。每个配有不同的地址码，用户所发射的载波既受基带数字信号调制，又受地址码调制。

跳频技术可以实现跳频多址：不同的用户使用不同的跳频图案，这样可以实现共享频段资源进行通信。下图就是不同用户以不同图案通信时的跳频图案。跳频有一定几率碰撞(两个发射器使用了同一个频率)，就是下图绿色的点点。通过对伪随机码进行设计，可以把跳频碰撞的概率控制得很小。

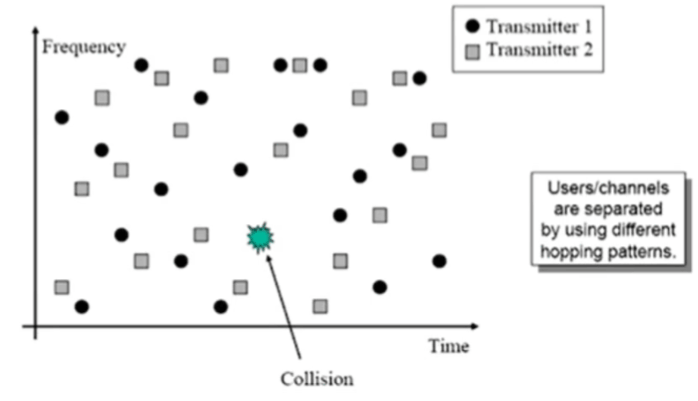
直接序列扩频（DSSS）

DSSS信号的调制与解调

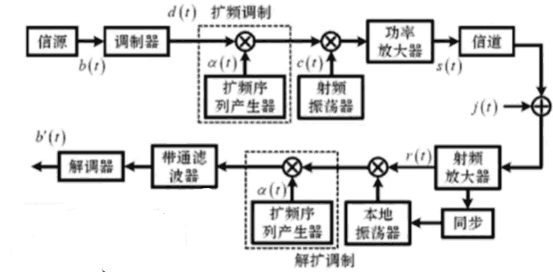
直接序列扩频使用扩频码(又称扩频序列、PN序列)，直接对基带信号进行频域扩宽。如下图就是一个对Bipolar NRZ信号扩频调制的例子。绿色的是频率更高的扩频码，由扩频序列产生器产生。将基带信号与扩频码相异或，即可得到扩频信号。解调时，在本振信号相干得到中频信号后，再使用同样的扩频信号相干（这个过程称为解扩），即可恢复基带信号。

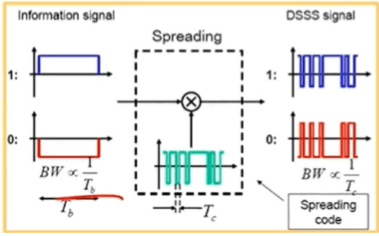扩频的时域、频域对应图像如下图所示：

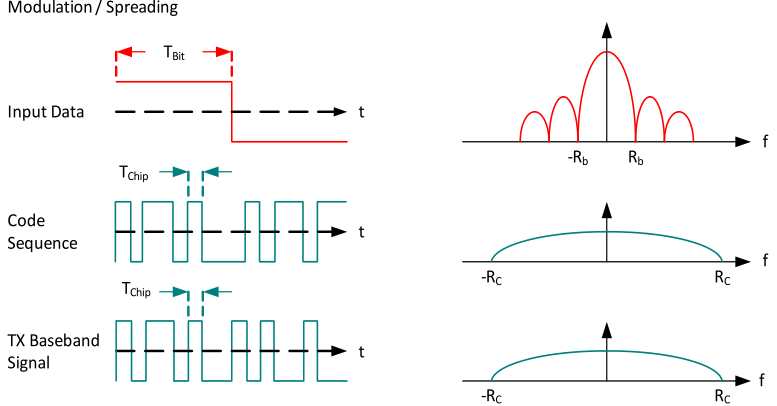
一个完整的扩频、解扩过程如下图所示：

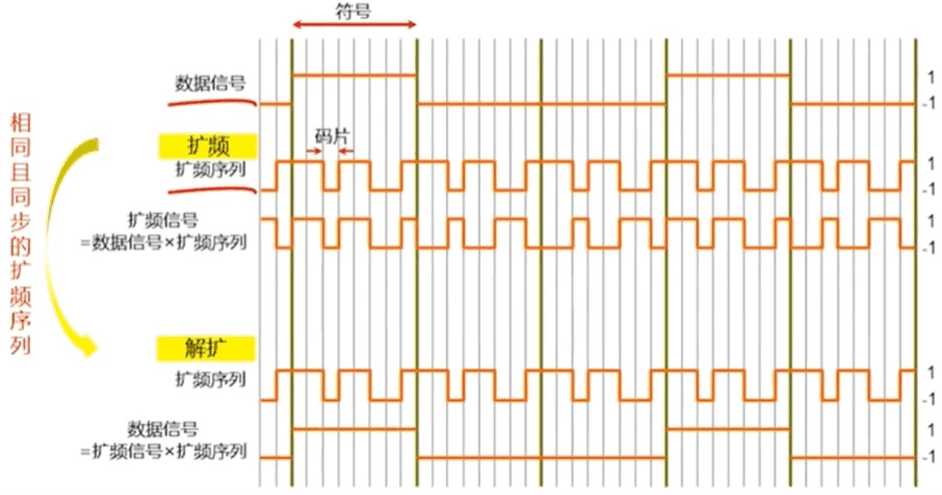
扩频增益/扩频因子 Spreading Factor

下列定义式中，Rc为直扩码速率；Rb为信息码速率。T是其对应单的持续时间（$T=1/f$）。

$G=10lg(\frac{扩频后的信号频率}{原始信号频率})=10lg(\frac{R_C}{R_b})=10lg(\frac{T_b}{T_C})$

G就是扩频增益。Rc/Rb即为扩频因子也称扩频码长度、带宽扩展因子

例如，原始信号频率为1MHz，扩频后为128MHz，则扩频因子$SF=128$ (部分地方直接认为扩频因子就是增益G，其实就是是否取对数的区别)

一般来说，扩频序列越长，扩频倍数越大，扩频增益越大

直扩信号优点和及其原理

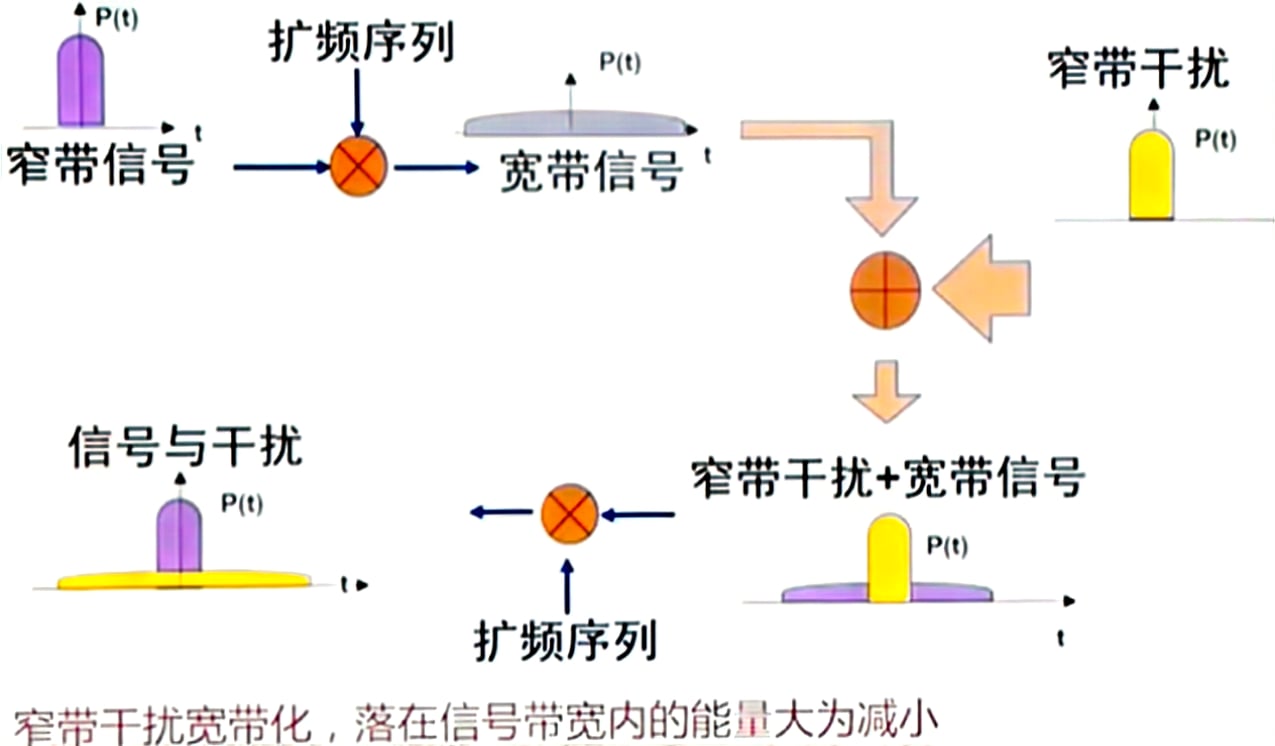
直扩通信抗窄带干扰的原理

一个原始的窄带信号，在经历扩频序列扩频之后，其能量不变(频域面积不变)，而频域展宽。
在传输时叠加了窄带噪声信号（例如来自其他通信系统的通信信号）
解调时再次用扩频码相干，延展频域扩频信号的恢复成窄带信号，而对叠加的窄带噪声信号，则是进行了一个扩频的过程。
在经历Bandpass filter的时候，噪声信号大部分功率可被滤除掉

1705249284302

直扩通信抗多径效应的原理

受多径效应影响，接受到的信号由多个不同时延和相位的原始信号构成（来自不同传输路径）

在单一解扩支路的情况下，通过调整解扩码的同步，可以只解扩振幅最强的一路信号，其他路径的信号在通过滤波器时就会被滤除
在多个解扩支路的情况下，接收端解扩码分别和来自不同路径的信号对齐，将其解扩分离。最后再将解扩出的多路信号相位时延对齐后叠加，恢复原始信号。

直扩信号抗劫获的原理

直扩信号频带很宽，功率谱密度很低。如果在接收机输入端，直扩信号的功率谱密度低于或与接收机热噪声功率谱密度相当，则接收机一般发现不了直扩信号(隐藏在噪声中)。

直扩信号的保密性

接收端只有采用与发射端相同且同步的扩频序列，才能实现对直扩信号的解扩，恢复出发送信号而扩频序列具有随机特性，破译难度大直接序列扩频技术首先应用于军事通信

直接序列扩频下的码分多址

不同用户采用不同的扩频序列，而这个扩频序列恰好就充当了码分多址里面地址码的作用。对某一个用户来说，他的接收机只能解扩对应扩频序列的信号，而其他用户的信号因为扩频序列不同，无法解扩，类似噪声。所以虽然看起来直扩通信每个用户看似占用频率很宽，但由于是共享不是独享，所以频谱利用率也很高的

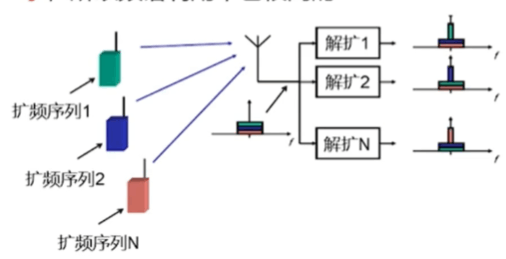
扩频序列（扩频码）

由前面介绍的直扩信号可以看出，我们希望扩频序列：

近似于随机信号有良好的自相关特性（可有效提取自身信号），很小的互相关特性（不同扩频序列间干扰小）
有尽可能多的码(序列个数，就是不重复的码长度)
下面是常见的扩频序列

m序列

m序列又称最长线性反馈移位寄存器序列，它是由多级移位寄存器通过线性反馈(就是下图这些摩尔加的抽头)产生的最长的码序列

对于n级的移位寄存器发生器所能产生的最大长度的码序列为$2^n -1$位（没有全0状态，因为一旦去了全0状态就无法游动到其他状态）

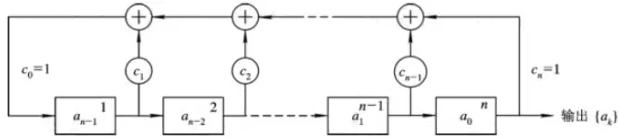
不同初始状态的移位寄存器，只会产生不同相位的扩频序列，无法产生不同的扩频序列；不同的扩频序列需要通过改变抽头结构来产生。而且并不是所有抽头组合都能产生m序列，只有特殊的组合才可以。

m序列有良好的自相关性，较小的互相关性的优点

对于n位的m序列，它能产生的序列个数可由如下公式计算：(其中$\Phi$是欧拉数)

$\frac{\Phi(2^n-1)}{n}$

计算可以发现，5级移位寄存器产生的$2^5 -1=31$位长度的m序列，只有6个。

因此，m序列具有数量较少的缺点

总结：m序列，优点：有良好的自相关性，较小的互相关性；缺点：m序列具有数量较少的缺点

M序列

m序列又称最长非线性反馈移位寄存器序列。M序列在m序列的基础上，加入了全0状态检测器，使其离开全0状态。

对于n个移位寄存器，可以产生$2^n$位的M序列

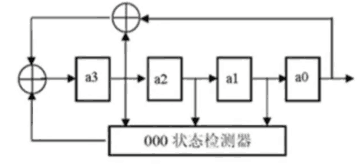
n级M序列的个数可以用如下公式来计算

$2^{2^{n-1}-n}$

在同为5级的时候，M序列可以产生2048个。因此M序列序列数量远大于m序列，但M序列的自相关性和互相关性又不如m序列

Gold序列

Gold序列将两个m序列作为优选对，把两个m序列的输出结果进行摩尔加。

它具有良好的自相关性，不明显的互相关性，构造简单因此获得广泛应用

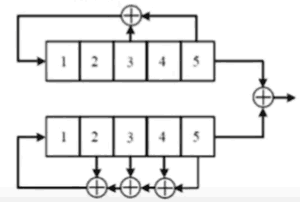
啁啾扩频/线性调频扩频(CSS)

啁啾($zh\overline ou ji\overline u$)

啁啾是频率随时间增加（up-chirp）或减少（down-chirp）的信号，其基本定义式如下：

$x(t)=sin(\phi(t))$

可以看到啁啾使用相位的移动来控制震荡频率，其相位是一个与 $t$ 有关的函数。在这个表达式下，瞬时角频率 $\omega$ 也就成了$\phi$ 的变化速率，即对$\phi(t)$求导。

$\omega(t)=\frac{d\phi(t)}{dt}$

再根据 $\omega$ 和 $f$ 的关系，可以写出频率表达式：

$f(t)=\frac{\omega(t)}{2\pi}$

类似于“角加速度”的概念，定义一个瞬时角啁啾系数(instantaneous angular chirpyness) $\gamma(t)$，单位：$rad/s^2$

$\gamma(t)=\frac{d^2\phi(t)}{dt}=\frac{d\omega(t)}{dt}$

instantaneous angular chirpyness 定义的是瞬时角频率的变化率，将角频率转化为频率，就得到的 instantaneous ordinary chirpyness $c(t)$ (定义为瞬时频率的变化率)

$c(t)=\frac{\gamma(t)}{2\pi}=\frac{df(t)}{2\pi}$

线性啁啾

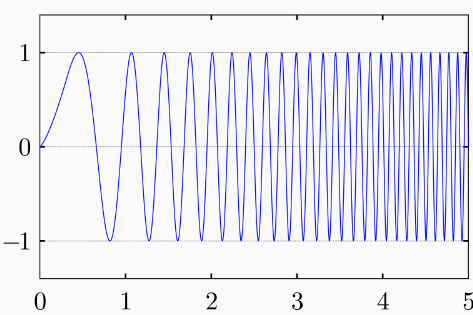
线性啁啾是指的瞬时频率$f(t)$随时间呈线性变化，下式中c是啁啾率(chirp rate)，是一个常数，表达式为$c=\frac{f_1-f_0}{T}=\frac{\Delta f}{\Delta t}$

$f(t)=ct+f_0$

转化成基本定义式中的相位的表达形式:

$\phi(t)=\phi_0+2\pi\int_0^tf(\tau)d\tau=\phi_0+2\pi(\frac{c}{2}t^2+f_0t)$

其中$\phi_0$表示初始相位

指数啁啾

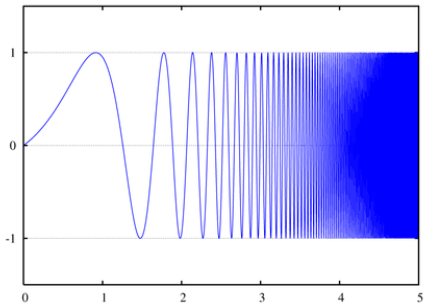
指数啁啾的定义为：

$f(t)=f_0k^{\frac{t}{T}}$

它具有如果$t_1$和$t_2$间时间间隔$T=t_2-t_1$是常数，$f_2(t)/f_1(t)$也是常数的性质。

相位表达式如下：

$\phi(t)=\phi_0+2\pi\int_0^tf(\tau)d\tau=\phi_0+2\pi f_0(\frac{k^{\frac{t}{T}}-1}{ln(k)})$

双曲啁啾

双曲啁啾定义为：

$f(t)=\frac{f_0f_1T}{(f_0-f_1)t+f_1T}$

其相位表达式为：

$\phi(t)=\phi_0+2\pi\int_0^tf(\tau)d\tau=\phi_0+2\pi \frac{-f_0f_1T}{f_1-f_0}ln(1-\frac{f_1-f_0}{f_1T}t)$

除此之外，还有对数啁啾，二次(^2)啁啾等，都是指的其频率的变化呈现对数、二次的关系。

啁啾扩频

由上方啁啾信号得知，啁啾信号频率随时间变化，也就是说，在频域来看，这个信号自带“扫频/扩频” 的特性。

如果说使用这个信号来作为载波，调制信号，那么这么信号的带宽也就被扩宽了。这就是啁啾扩频的原理。啁啾扩频利用了其频率在整个带宽上线性变化的正弦脉冲信号来传输信息，因此不需要任何伪随机序列。

举个例子，下图这个调制模块（802.15.4a中定义的超带宽UWB调制，Chirp-UWB）：二进制信号先转化为差分信号后进行QPSK调制，再对QPSK信号进行进行啁啾调制来扩频得到QCSK信号。

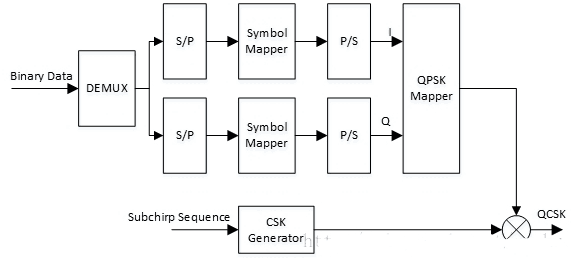
在这个例子中，调后的一个啁啾符号（Chirp Symbol）由4个啁啾脉冲（subchirp）构成，每个啁啾脉冲又可以携带一个QPSK信号。从而一个啁啾符号可以携带4个QPSK码字。

由于不能让这个啁啾信号占用无限的带宽，所以会对这个啁啾载频规定一个频率上限$f_H$和一个频率下限$f_L$，以up-chirp为例，它由起始频率$f_0$开始，随时间攀升，如果在自身持续周期内超过了$f_H$，那它将回到$f_L$,再继续爬升如下图所示(下图横坐标为时间$t$,纵坐标为频率$f$)。

---CHAPTER END---