Control-Systems-Part2-Lectrue5-PID调谐和数字补偿器设计
PID控制器调谐
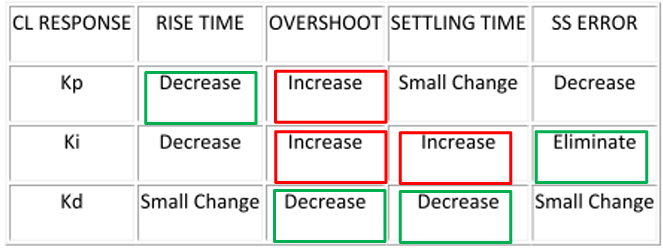
PID三个部分对系统响应的贡献
在Part1中详细介绍和分析过PID控制器,这里主要介绍一个调谐原则。回顾一下,PID的通式是:
写成并联形式是:
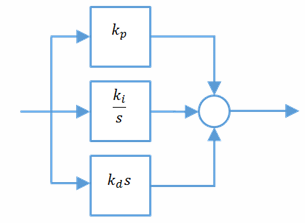
写成标准形式是:
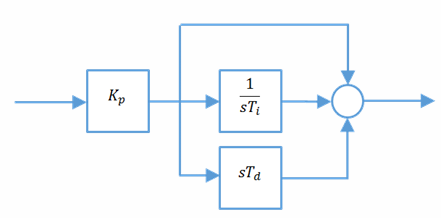
PID控制器会给系统引入一个位于原点的极点,和2个零点。由前面介绍的零极点分析系统响应的法则,可以导出其各个部分对系统瞬态响应的贡献:
$K_p$的贡献是:
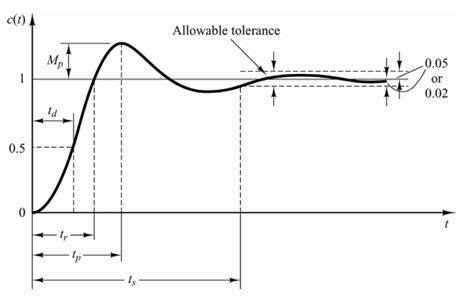
- 减少rise time $t_r$
- 但是无法消除稳态误差
决定响应速度和力度,过小响应慢,过大会产生振荡,是I和D的基础。
$K_i$的贡献是:
- 消除稳态误差
- 但是会削减瞬态响应
- 会削减系统稳定性
在有系统误差和外力作用时消除偏差、提高精度,同时也会增加响应速度,产生过冲,过大会产生振荡。
$K_d$的贡献是:
- 增加稳定性(包含减少过冲 overshoot $M_p$ 和 改善瞬态响应)
- 但是会导致系统对高频噪声更敏感
抑制过冲和振荡,过小系统会过冲,过大会减慢响应速度。另外一个作用是抵抗外界的突发干扰,阻止系统的突变
总结为下表:
PID调谐
广泛流传的经验法整定
所谓PID调谐,就是在系统的过冲、上升时间、下降时间、稳态误差之间取一个可以接受的平衡。
有一些广泛流传的PID调谐的口诀,例如《化工自动化》一书中的参数整定口诀:
参数整定寻最佳,从大到小顺次查。先是比例后积分,最后再把微分加。曲线振荡很频繁,比例度盘要放大。曲线漂浮绕大弯,比例度盘往小扳。曲线偏离回复慢,积分时间往下降。曲线波动周期长,积分时间再加长。 理想曲线两个波,调节过程高质量。
齐格勒-尼科尔斯方法(Ziegler-Nichols method)
齐格勒-尼科尔斯方法的调试方式为:
- 首先将积分和微分增益设置为0,然后比例增益从零开始逐渐增加,直到到系统临界稳定条件(marginal stability),此时控制器输出值以恒定值振荡。拿到临界震荡的下critical gain $K_c$和critical frequency $\omega_c$,$T_c=\frac{2\pi}{\omega_c}$
- 根据不同系统的要求,遵照下表找一个合适的经验值
| 控制类型 | $K_p$ | $K_i$ | $K_d$ |
|---|---|---|---|
| P | $0.5K_c$ | - | - |
| PI | $0.45K_c$ | $0.54K_c/T_c$ | |
| PD | $0.8K_c$ | - | $0.1K_cT_c$ |
| 经典PID | $0.6K_c$ | $1.2K_c/T_c$ | $0.075K_cT_c$ |
| Pessen Integral Rule | $0.7K_c$ | $1.75K_c/T_c$ | $0.105K_cT_c$ |
| 部分过冲 | $0.2K_c$ | $0.4K_c/T_c$ | $0.066K_cT_c$ |
这个表上面的值都是经验值,不同地方可能不一样。上表是简中互联网广泛流传的表。
Dr.Huda PPT上的法则是这样:(注:$T_i=\frac{K_p}{K_i}$,$T_d=\frac{K_d}{K_p}$)
| 控制类型 | $K_p$ | $T_i$ | $T_d$ |
|---|---|---|---|
| P | $0.5K_c$ | - | - |
| PI | $0.4K_c$ | $0.8T_c$ | - |
| PID | $0.6K_c$ | $0.5T_c$ | $0.125T_c$ |
实操PID只需要套公式就行了,但是考试要考虑的事情就很多了
实际操作时调PID依照积分、微分、比例三个部分对系统瞬态响应的影响来调即可,不一定会完全遵照这些经验表格。
模拟补偿器数字化
模拟补偿器数字化法设计可以概括为如下三步:
- 按照系统要求设计模拟补偿器
- 通过下面介绍的映射规则将它数字化
- 代入数字控制系统的采样周期,检查系统响应是否满足要求。如果不满足,重复步骤1和2。
模拟系统离散化的映射方法:
- 前向欧拉法(Euler’s forward method):$s\approx\frac{z-1}{T}$
- 后向欧拉法(Euler’s backward method):$s\approx\frac{z-1}{Tz}$
- 双线性法/塔斯汀法(Tustin’s method/bilinear transformation):$s\approx\frac{2}{T}\frac{z-1}{z+1}$
- 零阶保持器(Zero-Order hold):$C(z)=(\frac{z-1}{z})Z[\frac{C(s)}{s}]$
举个例子:Tustin’s method离散化Ziegler-Nichols method调谐的PI控制器
已知:系统的传输函数和框图为,其$K_c=201,\omega_c=14.2$:
要求:使用Ziegler-Nichols method设计PI控制器,采样间隔为0.1s,并使用(i)Tustin method (ii)ZOH将其数字化
step1:使用Ziegler-Nichols method为系统调谐PI控制器
因此:
step2-(i):使用Tustin method 将系统离散化
将$s\approx\frac{2}{T}\frac{z-1}{z+1}$代入$C(s)$
代入$T=0.1$
step2-(ii):使用ZOH将系统离散化
代入$T=0.1$
根轨迹设计法
引入
$F(z)$的模长和角度可以表示为多个复数贡献的形式,例如下面这个:
假设现在有一个系统函数,它在$F(z)=(z+3)$。那么当$z=2+2j$时,系统函数的向量值为$(5+2j)$。
这里有一个很巧的事情:$(z+3)$的零点是$z=-3$。当$z=2+2j$时,系统函数的向量$(5+2j)$就等于从它贡献的零点连到$z+zj$的向量,如下图
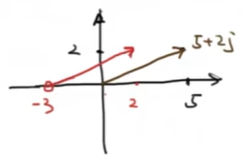
假设一个系统函数有好几个零极点,例如$F(s)=\frac{s+2}{s(s+1)}$,那么当s为某一个特定值时,系统函数内每一个复数分量就可以表示为他们贡献到零极点到这个特定s的连线,叠加在一起就是系统函数的值。例如当$s=-1+\sqrt{3}j$时
系统有零点s=-2,有极点s=0,-1。从-2,-1,0连接三条线到s,如下图所示
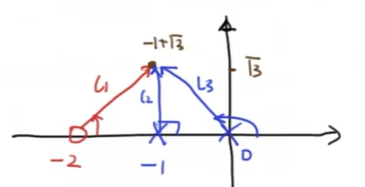
可以分别求得其长度为$l_1=2,l_2=\sqrt{3},l_3=2$;其角度为$\theta_1=\frac{\pi}{3},\theta_1=\frac{\pi}{2},\theta_1=\frac{2\pi}{3}$
按照上面介绍的系统函数内各个复数叠加的理论,可以求得这个系统函数$|F(s)|=\frac{2}{2\times\sqrt{3}}=\frac{\sqrt{3}}{3}$,$\angle F(s)=\theta_3-\theta_2-\theta_1=-\frac{5}{6}\pi$
在前一章节从特征函数的角度理解根小节中提到过,如果要使得某种情况(z或者s等于某个定值时)的特征函数成立,其CLTF$F(z)$必须满足:
- $|F(z)|=1$
- $\angle F(z)=\pm180^\circ(2k+1),k=0,1,2..$
那么,理论上来说,我们可以给系统安插一个通式如下的补偿器,来使得$s$或$z$为某个人为指定的定值时,特征方程成立,即,满足上面的条件。此时系统的特征方程有一个根就会出现在这个人为指定的位置。
由于系统的特征方程根位置和系统当前的响应有直接关系,因此可以通过将对系统响应的需求转化为对根出现在某个点的需求。然后根据需求按照上面的法则设计补偿器。这就是根轨迹补设计法。
常用的转化公式为:(其中$\omega_d$为受阻震荡频率,$\omega_s$为采样频率,$\omega_n$为自然频率,$\zeta$为阻尼率)
举个例子
现有如下系统,要求其阻尼比$\zeta=0.5$,setting time $t_s=2s$
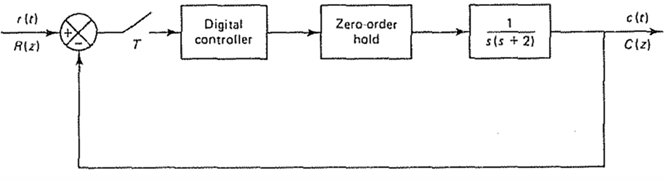
Step1:将响应需求转化为根需求
假设采样周期$T=0.2$验证一下它符不符合采样的经验法则(在笔记ch4内介绍):
因此符合经验法则的要求。套用前面的转化公式:
这就是我们补偿后的人为确定的z,我们希望当z等于这个值时,特征方程成立。将其写为复数形式:
step2:将ZOH和模拟系统构成的新传输函数解出
这里直接套用前面介绍的ZOH输入模拟系统的转化公式:
代入$T=0.2$
Step3:计算系统现有零极点的角度贡献
那么这个系统现在有:
- zeros:-0.8760
- poles:1,0.6703
我们希望系统达到这个状态:($P=0.5158+j0.4281$)
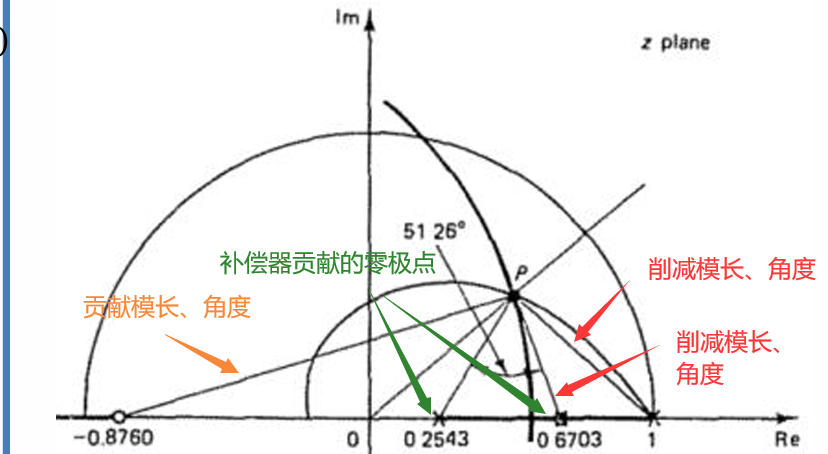
先计算系统自带的零极点的角度贡献:
z=1的极点贡献了:(这里变成正数是因为它转过180度了,由复数角度的定义得来的。详见复变函数)
z=0.6703的极点贡献了:
z=-0.8760的零点贡献了:
Step4:计算系统还需要的角度(补偿器提供的)
要使得特征方程的根出现在我们想要的这个地方,需要让当z=P时,特征方程成立。也就是说OLTF的角度要满足$\angle F(z)=\pm180^\circ(2k+1),k=0,1,2..$,也就是系统自带的这些角度贡献+补偿器的角度贡献要满足$\pm180$度
补偿器通式为$K\frac{z+\alpha}{z+\beta}$,会引入一个极点和一个零点。为了简化计算,我们让它的零点贡献和系统自带的一个极点贡献抵消掉。这里取$z+\alpha=(z-0.6703)$来抵消,即$\alpha=0.6703$($-70.16^\circ$极点贡献被抵消了)
现在我们只需要计算$C(z)$中的这个极点,让系统角度满足即可
如果取$-180$,那么补偿器极点就需要贡献$-180+138.52+17.10=58.58^\circ$
至此我们得到了补偿器的$\alpha$和$\beta$参数:
Step3:计算系统现有零极点的模长贡献
系统现有的模长贡献有:(目标点:$P=0.5158+j0.4281$)
分子(z+0.8760)贡献了:$\sqrt{(0.5158-(-0.8760))^2+(-0.4281)^2}=\sqrt{(1.3918)^2+(0.4281)^2}$
分母(z-0.2543)贡献了:$\sqrt{(0.5158-0.2543)^2+(-0.4281)^2}=\sqrt{(0.2615)^2+(0.4281)^2}$
- 分母(z-1)贡献了:$\sqrt{(0.5158-1)^2+(-0.4281)^2}=\sqrt{(0.4842)^2+(0.4281)^2}$
$|F(z)|=1$,即:
至此,我们得到了补偿器的表达式: