智能系统设计-Part1-模糊系统

引入

在前面的ANN中，机器可以自己通过学习来找到“机器认为”的答案。

但是在现实世界中也有一群专家，他们解决问题靠的是“已有知识”，他们先学习并储备了一些知识库，在遇到对应问题的时候就调用对应的知识库。

将这种解决问题的方式在计算机中进行描述和调用，就是所谓模糊系统（Fuzzy System）。

但是专家在判断是什么问题时，通常接受的是模糊的描述。例如这个人非常高，那么你大可能觉得这个人在一米八往上接近一米九。说这个天很热按你大可能觉得现在有30度往上。这些描述都是基于人类语言的模糊描述，指明的是大概率的一个区间。同样地，在解决问题上，专家也是靠着不精确的输入，去猜测套用什么方法解决的可能性最大，然后去尝试。

但是这样就出现问题了，计算机使用的是布尔逻辑，即非黑即白的逻辑，它可以以180为一个界限，认为180以上的人算作高，180以下的人算作矮，但是如果有一个人有179,它其实也是算高的，但是会被传统的布尔逻辑和160判到一桌上去。

模糊逻辑，模糊集和隶属度

模糊系统就是为了来解决这个问题的，它提出了“模糊逻辑（fuzzy logic）”的概念，在模糊逻辑下，事情不是非黑即白，而是具有一定概率的。

在数学上，集合的定义是由一个或多个确定的元素所构成的整体。个子高的人就可以被视作一个集合，个子矮的就是另一个集合。在传统集合的定义下，一个人要么属于个子高这个集合，要么属于个子矮。但是模糊集允许它同时部分属于这两个集合（使用概率描述），例如下面这个里例子，179的人有0.78的概率属于高个子的人，而不是二值逻辑那样直接判定为和152坐一桌了。模糊系统相较于布尔系统，能提供更精确的分类。

与传统集有边界条件一样，模糊系统也有边界条件，即某一条件数值和隶属于这个集合的“度”的关系。例如下面这个例子：将这种隶属于身高的群体的概率，称为隶属度（degrees of membership）。

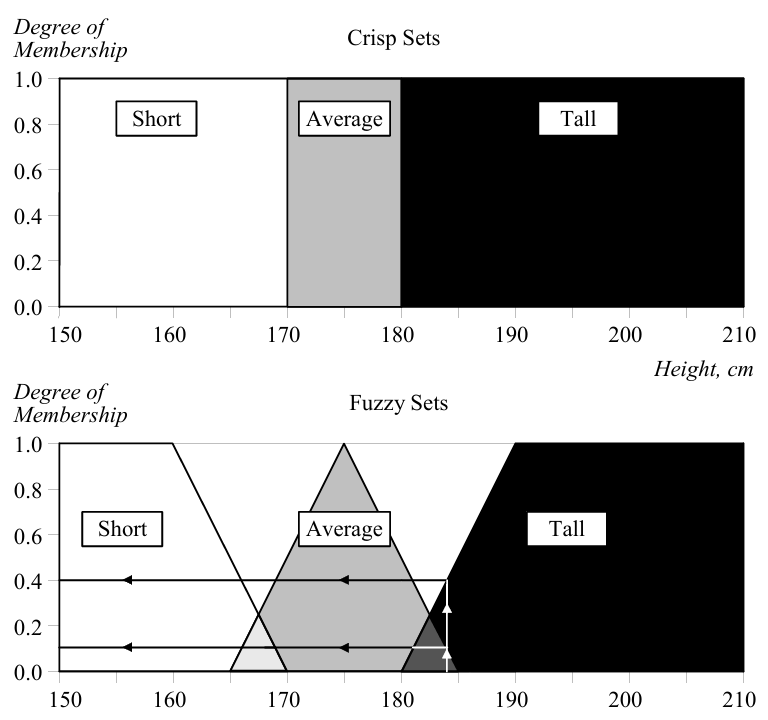
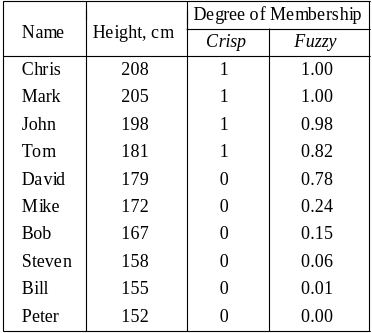
通常，为了方便，将某一元素针对某些模糊集的隶属度记为：

$$A=\mu_A(x_i)/x_i+...+\mu_A(x_i)/x_i$$

其中，$\mu_A(x_i)$模糊集A在点$x_i$上的隶属度

语言变量（linguistic variables）

因为fuzzy system是专家系统，因此有一些使用人类语言描述的“经验主义”条件。例如“风浪越大，鱼越贵”就可以表示为：

IF wind is strong, THEN price is high

这样的表达式被称为语言变量（linguistic variables）。

语言限定词(linguistic Hedges)

人类在自然语言描述东西时，还会加入一些修饰词，例如very, extremely, slightly这样的。这些词被称为hedges。

这些词可能让模糊集的边界变得非线性，例如说一个人extremely high，可能它是190+，从185+到190+就上升了5cm，但是能到190+的人却很少。下图就是这样的一个例子，被hedges修饰之后，每个模糊集合的边界不再是之前的线性边界。

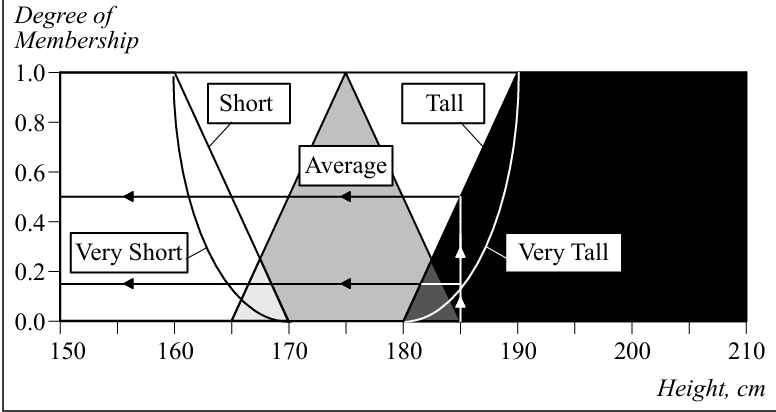
下面是一些常用的修饰词和他们对应的边界函数：

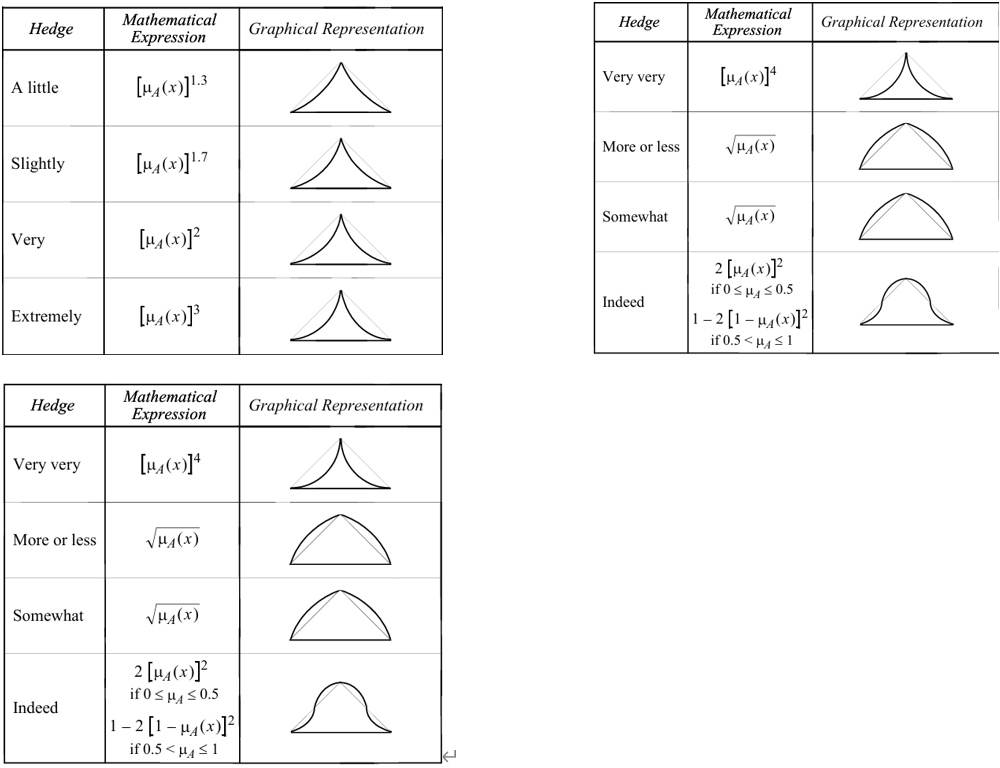
模糊集的基本计算和性质

与传统的集合有交集、补集、并集等等计算，包含、不包含等关系一样，模糊集也有一套计算规则和自己的性质。

基本定义

补集（complement）

传统的求补是求不属于集合A的元素。类似的，模糊集的求补是求不属于集合A的元素的概率，因此补的定义为：

$$1-\mu_A(x)$$

图像上来看是：

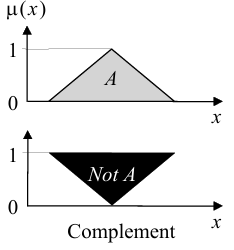
可以看到，当属于集合A概率为1时，不属于集合A的概率为0。属于集合A的概率为0时，不属于集合A的概率为1。

交集(Intersection)

传统集合定义中，元素某一范围内既属于集合A，又属于集合B的部分被称为交集，其边界同时被A和B约束。类似地，如果一个元素在某一范围内可以部分属于A，又部分属于B，其隶属度同时被A和B约束，则该范围就是A与B的交集。图像上是下图：

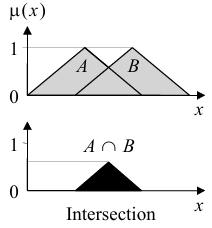
从上图可以看到，交出来的部分被A和B中隶属度较小的一方所约束，因此计算表达式为：

$$\mu A\cap B(x) = \mu A(x)\cap \mu B(x) = min[\mu A(x),\mu B(x)]$$

并集(Union)

传统集合定义中，并集是指某一元素在该范围内属于A或B任意一方或双方。类似的，在模糊集中，并集是指的在A或B任意一方隶属度范围之内。图像上看是这样：

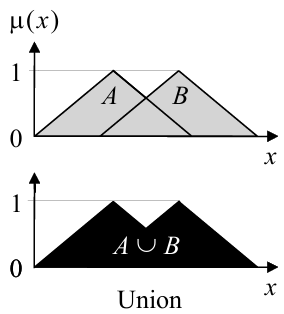
并出来的部分被A或B中拥有较大隶属度的一方所约束，因此其计算表达式为：

$$\mu A\cup B(x) = \mu A(x)\cup \mu B(x) = max[\mu A(x),\mu B(x)]$$

模糊集的特性定义

等价(Equality)

传统集合中当A集合和B集合完全重叠时，说A和B集合等价。而在模糊集里面，当某一元素在集合A的各项元素中的隶属度完全等于集合B时，则集合AB等价。例如$A=0.3/1+0.5/2+1/3$，$B=0.3/1+0.5/2+1/3$

包含(Inclusion/Containment)

传统集合的对包含的定义是A集合完全在B中。类似地，如果某一元素对A集合在定义区间内的所有元素的隶属度小于B集合，那么A集合就是B集合的子集。图像上看起来是这样：

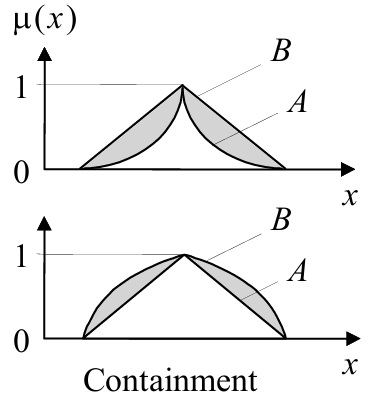
A和B两个大集合内可以有多个元素（也就是特定点的值），体现元素上就是某一元素在集合A下，对各个元素的隶属度均小于等于对B的。数学表达式为$\mu_A(x)\leq\mu_B$。例如$A={0.3/1+0.5/2+1/3},B={0.5/1+0.55/2+1/3},A\subseteq B$

基数(cardinality)

传统集合的基数指的是一个集合内有多少个元素，也称为势。在一个集合内有3个元素，那么该集合的基数就是3。模糊集的基数是指的某一模糊集内各元素隶属度的和。

例如$A={0.3/1+0.5/2+1/3}$，则A的基数$card_A=0.3+0.5+1=1.8$；$A={0.5/1+0.55/2+1/3}$，则B的基数$card_B=0.5+0.55+1=2.05$

空模糊集(Empty Fuzzy Set)

当某个集合不隶属于元素时，它是空模糊集，也就是$\mu_A(x)=0$，例如$A={0/1+0/2+0/3}$

截集(alpha-cut)

一个模糊集合的截集（alpha-cut）指的是这个集合内各元素隶属度大于某个阈值的部分，使用$集合_{阈值}$的格式来表达。模糊集存在半隶属的定义，而其截集却是一个经典集合，只存在隶属和不隶属的关系。下图展示了模糊集A的在阈值$\lambda$下的截集。

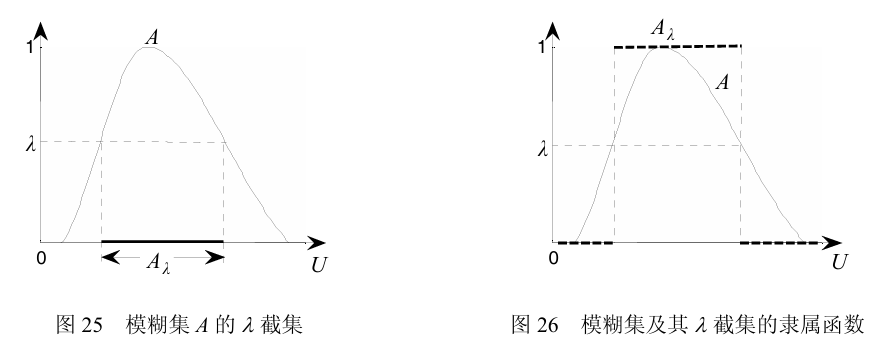
例如假设有模糊集$X=\{1,2,3\}$，模糊集A是X的子集，$A=\{0.3/1+0.5/2+1/3\}$

则对A的alpha-cut是：

$A_{0.5}=\{2,3\}$

$A_{0.1}=\{1,2,3\}$

$A_{1}=\{3\}$

模糊集的正规性(normality)和高度（height）

如果在一个模糊集内，有一个元素的隶属度达到1（最大隶属度），则称该模糊集是正规的（normal），否则称为非正规（subnormal)。下图是正规模糊集（A）和非正规模糊集（B）的隶属函数图。

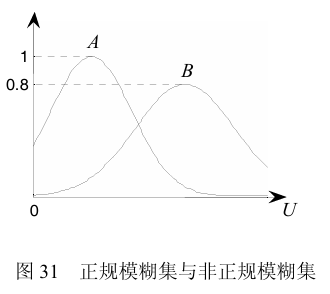
同时，在模糊集内拥有最高隶属度的元素被称为该模糊集的高度(height)，$height(A)=max_x(\mu_A(x))$

支集（Support），核（Core）和边界（Bound）

支集(support)：模糊集内隶属度不为0的元素，中文又称支撑集。

核(Core)：模糊集内隶属度为1的元素

边界(Bound)：模糊集内隶属度位于0-1之间的元素

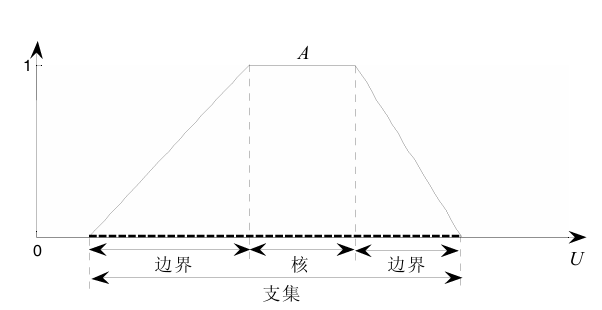
例如$A=\{1/a,0.3/b,0.2/c,0.8/d,0/e\}$

• 支集：$supp(A)=\{a,b,c,d\}$
• 核心：$core(A)=\{a\}$
• 边界：$bound(A)=\{b,c,d\}$

模糊集的数学运算

乘法

假设系数为a，对于模糊集A，$aA=\{a\mu A(x)\}$。

例如a=0.5, $A=\{0.5/a,0.3/b,0.2/c,1/d\}$，$aA=\{0.25/a,0.15/b,0.1/c,0.5/d\}$

平方

假设指数为a，对于模糊集A，$A^a={\mu_A(x)^a}$

例如a=0.5, $A=\{0.5/a,0.3/b,0.2/c,1/d\}$，$A^a=\{0.25/a,0.09/b,0.04/c,1/d\}$

逻辑运算：与或非

Max-Min逻辑组合法

对于传统的集合，与运算等于求交集，或运算等于求并集，非运算等于求补集。同样的，对于模糊逻辑也是如此。

也就是说，按照前面的介绍的求交并补的规则：

• AND就是求A和B中隶属度较小的一个（min）
• OR就是求A和B中隶属度较大的一个（max）
• NOT就是求A的补集（$1-\mu A(x)$）

这样的求法是max/min组合法，是最常用且简单，后续介绍的Max-Min inference就是基于该种组合。除了这个之外，还有其他的逻辑算法。例如集合取交集的算法（统称T-norm）就有minimum T-norm(也就是上面提到的取最小值)，product T-norm（也就是交集是两个集合实数的点乘），Lukasiewicz T-norm（$max\{0,a+b-1\}$）。

模糊系统设计

一个模糊系统的需要将数据数据根据模糊规则分析之后，得到一个输出；其中根据模糊规则分析这一步可以拆分为两个部分：将输入的模糊逻辑根据逻辑规则库组合，再将其的结果映射到输出的模糊逻辑。这意味着模糊系统需要以下四个步骤：

1. 输入模糊化（Fuzzification）
2. 套用规则库（Rule evaluation）
3. 模糊输出逻辑聚合（Aggregation/composition）
4. 去模糊化（Defuzzification）

模糊推理流程（以Mamdani-style推理为例）

理论比较抽象。MATLAB的fuzzy system 给出了一个例子，非常形象：由餐厅的服务质量和食物质量来推算将获得多少比例的小费。在这个例子中，认为小费和有两个输入有关：食物和服务质量。

输入模糊化

这个过程是对输入数据进行量化，一般由统计学得到或专家/经验主义给出。

在这个例子中，对食物量化为delicious,fine,rencid三种品质；对服务量化excellient,good,poor三种品质。然后通过统计学去统计某一等级的食物有多少百分比的人认为好吃，多少百分比认为还行，多少百分比认为不好吃；服务同理。将统计学得到的数据拟合为连续的函数，即可得到下图的隶属度函数。

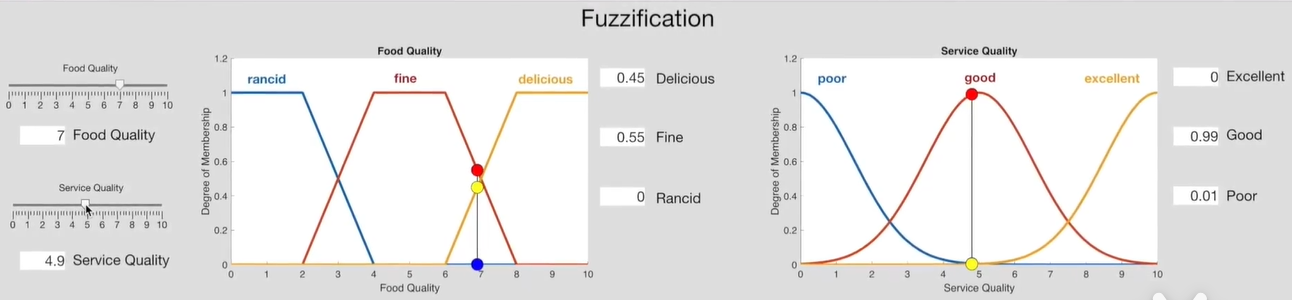
现在有一个质量等级为7的食物在服务等级为8的餐厅。根据上述隶属度函数，则各项隶属度为：

• delicious: 0.45; fine: 0.55; rancid: 0;
• excellent: 0.38; good: 0.15; poor: 0;

套用规则库

根据经验主义假设的规则库有：

IF service IS poor OR food IS rancid   THEN   tip IS low
IF service IS good  THEN   tip IS avergae
IF service IS excellent OR food IS delicious  THEN  tip IS high

按照前面逻辑组合运算章节的介绍，对上述规则使用Max-Min inference来转化为输出模糊逻辑：

• low = max(poor, rancid) = max(0,0) = 0
• average = good = 0.15
• high = max(0.38, 0.45) = 0.45

因此，输出low的隶属度为0，属于average的隶属度为0.15，属于high的隶属度为0.45。

输出逻辑的与聚合

输出模糊集Z有三个元素：low，average，high。根据经验/统计学，认为小费最最低是0元，最高为30元，模糊集的隶属度函数如下图所示。

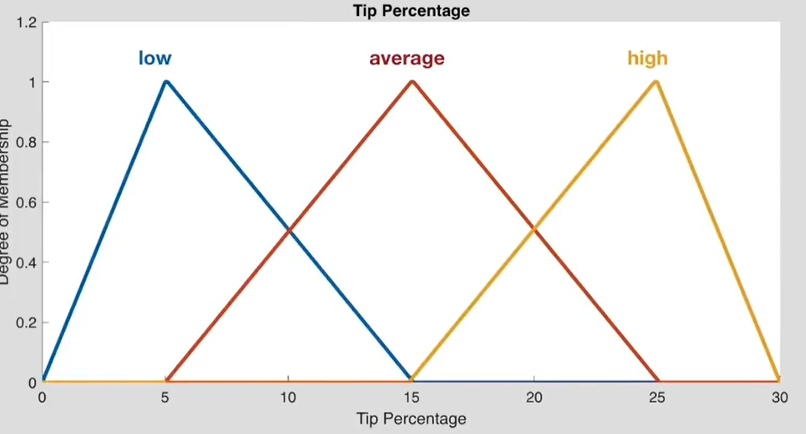
此时这个输入对这三个元素的隶属度分别为0, 0.15, 0.45。现在需要将这三个隶属度聚合为一个完整的图像。

有两种常用的方法，一种是clipping, 一种是scaling。clipping就是指直接填充原隶属度函数，例如对C2的隶属度是0.2，那么就直接把C2填充的0.2的位置。scaling是将原有隶属度函数等比例缩放，在0.2这个例子下，就是将原来的高度缩减为0.2倍。如下图所示。

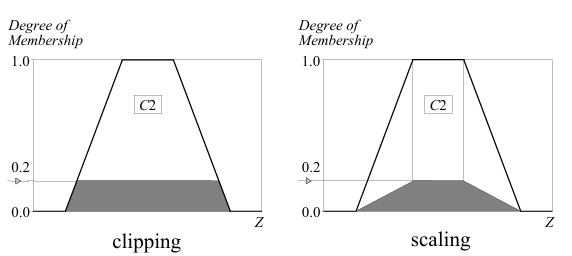
裁剪的计算更简单（特别是在去模糊化的时候），但会导致一部分信息丢失。缩放可以更好的保留原始形状，丢失信息较少，在模糊专家系统中非常有用。

这里以裁剪为例继续。

在将每一个元素的隶属度图像求出来后，将他们拼合在一起，就完成了输出逻辑聚合。如下图所示，给low填充0%，average填充15%，high填充45%，然后拼合在一起得到右侧图像。

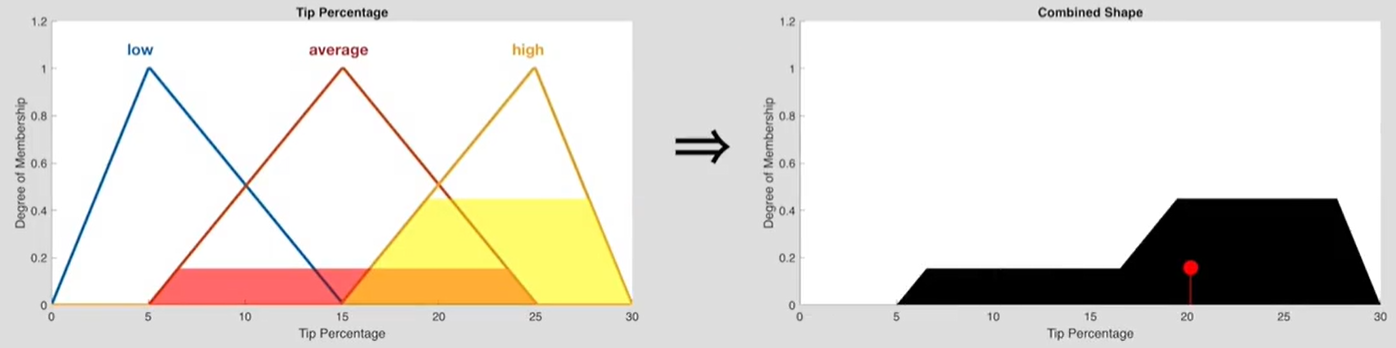
去模糊化

我们得到了输出的模糊逻辑图像，但是最后的输出需要是一个精确的数字，例如这次小费将会达到前80%的水平这样的数字。因此还需要将该图像去模糊化为一个精确数字。

同前面一样，去模糊化也有很多方式，最常用的是求质心点(centre of gravity)的方法。在上图这样的二维图像中，求质心点的通式为：

$$COG=\frac{\int_a^b\mu_A(x)xdx}{\int_a^b\mu_A(x)dx}$$

其中隶属度$\mu_A(x)$被抽象为了密度，可以想象图像是一条具有不同密度的线。

用一个离散的例子可以更好地观察这个公式：

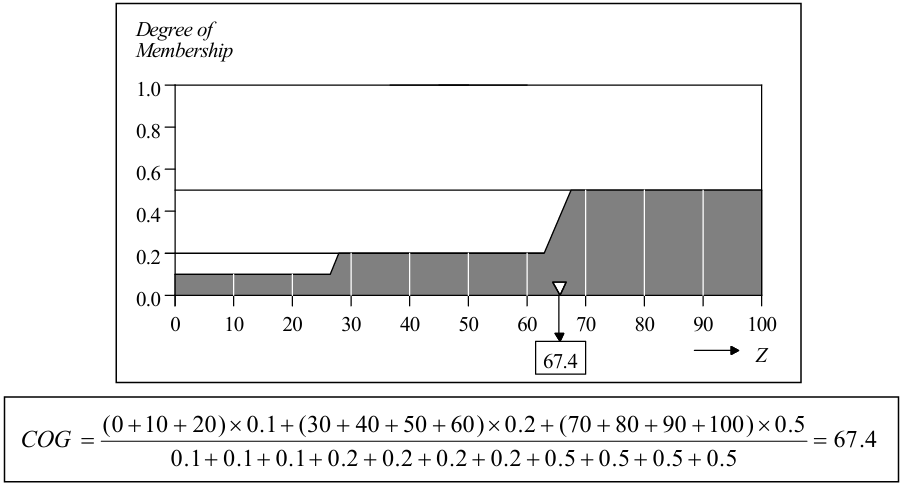
最后可以计算得出，得到的小费将可能会是20.2%

Sugeno推理

原理

上述这种输出模糊集同输入一样，使用隶属函数描述的被称为Mamdani推理。与之相对的还有一种Sugeno推理方式。在Sugeno的定义中，输出逻辑不再是一个函数，而是一个常数。例如

IF x IS A AND y IS B  THEN  z IS k

其中k是常数。

在Sugeno推理下，输出逻辑的聚合完全遵照clipping法则，如下图所示。

条件1：A3 OR B1 = max (0.0, 0.1) = 0.1，则将THEN的常数k1填充到0.1；其余条件同理

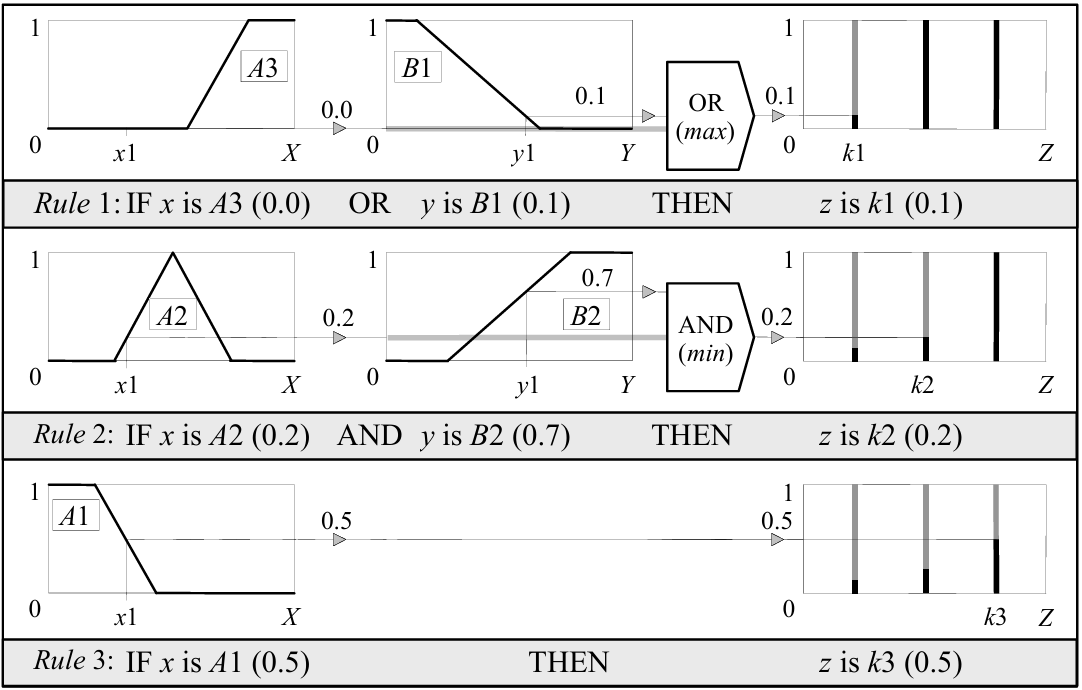
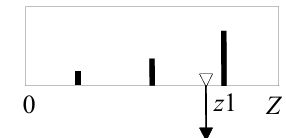
在去模糊化时，直接将他们加权求平均（Weighted Average, WA）即可，其中k1,2k,k3的值就是该点的权重，隶属度是该点的量，如下所示：

$$WA=\frac{\mu(k1)\times k1+\mu(k2)\times k2+\mu(k3)\times k3}{\mu(k1)+\mu(k2)+\mu(k3)}$$

与Mamdani的差异

相较于Sugeno，mandani可以能够以更直观、更人性化的方式描述专业知识。然而，Mamdani型模糊推理需要大量的计算负担。

Sugeno方法在计算上效率很高，并且可以很好地嵌入优化和自适应技术，这使得它在控制问题中非常有吸引力，特别是对于动态非线性系统。

自适应神经模糊推理系统

在前面提到，NN可以根据自我学习进化。而fuzzy system依托于fuzzy rules则是统计或经验模型，这使得其是一个不可改变的系统。而自适应神经模糊推理系统(Adaptive Neuro-Fuzzy Inference System, ANFIS)则结合了二者优点，又可以接受模糊的输入，又可以自我学习进化。

回顾一下fuzzy system, 它的输入又统计学或经验模型进行模糊化，然后使用Min-Max或T-norms之类的逻辑运算规则，依照rules将输入映射至模糊输出，最后聚合输出并去模糊化求出数值。

ANFIS与传统模糊系统有差异，它的模糊化操作并不是根据统计学或经验模型直接得出的，而是使用训练数据集自我习得的。rules也并非人为指定，而是具备所有输入rules的两两组合，例如有x和y两个输入，x 和 y分别有(A1 A2) 和 (B1 B2)两个元素，则rules就有A1 AND B1, A1 AND B2, A2 AND B1, A2 AND B2四种。输入到输出模糊集的映射，也就是THEN后面的东西也并非人类指定，而是自我学习完成。下面将会详细介绍。

下图是一个经典的2输入2 rules ANFIS模型。

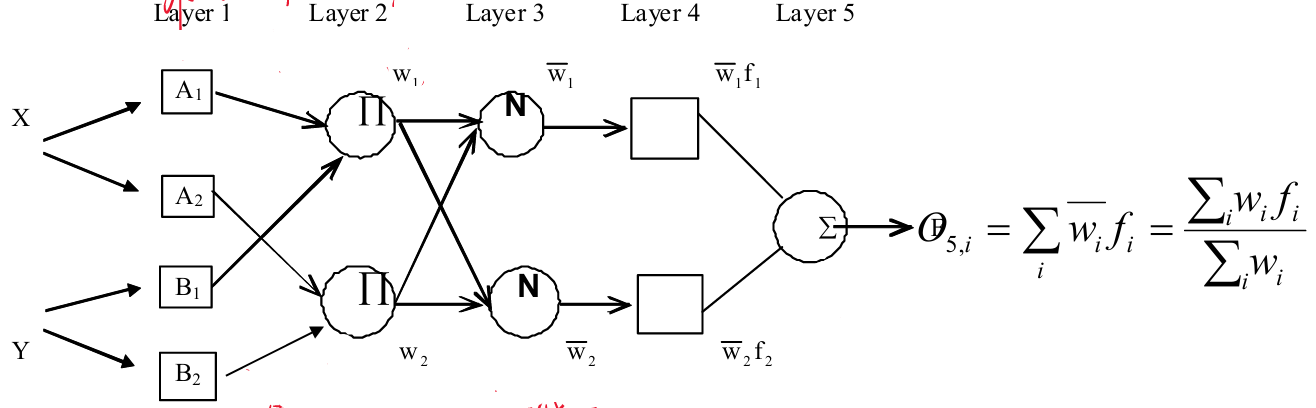
layer1（自适应层）：输入模糊化层。该层会预设一个贝尔函数(Bell function)作为隶属函数，其通式为

$$\frac{1}{1+\bigg|\frac{x-c_i}{a_i}\bigg|^{2b_i}}$$

图像如下所示。其中$a_i,c_i,b_i$被称为”Premise Parameters”会根据训练数据使用在后向传输使用梯度下降法（Gradient Descent）自我学习，以改变隶属函数形状。

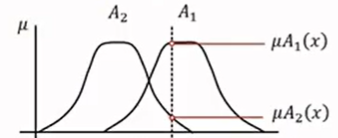
layer2（固定层）:触发强度层。该层会计算layger1中所有rule的两两AND组合，输出其“强度”。其AND运算并非之前介绍的minimum T-norm 法则，而是product T-norm法则，product T-norm直接计算两个集合值的实数乘机。例如上图$w1=A1\cdot B1$，如此计算得到的便是强度

layer3（固定层）:触发强度归一化层。该层旨在将第二层得到的强度数据归一化。以上图举例，归一化的公式为：

$$O_{3,i}=\overline w_i=\frac{w_i}{w_1+w_2}, i =1,2$$

其中$O_{3,i}$表示第三层的第i个output，例如$O_{3,1}=\frac{w_1}{w_1+w_2}$

layer4（自适应层）：计算规则输出层，该层使用上一层输出的$w_i$乘上函数$f_i$。$f_i$是一个自学习的函数，其通式为

$$f_i=c_0+c_1x_1+c_2x_2+...c_nx_n$$

对于上面合格例子，其式子就是$f_i=p_ix+q_iy+r_i$。其中$p_i,q_i,r_i$被称为consequent parameters，是训练优化的对象；x和y是输入的数据的值,。该层在前向传输时，使用LSE进行训练。

layer5（固定层）：去模糊化层，该层将4层的结果加起来，直接输出。

$$O_{5,i}=\sum_i\overline w_if_i$$

这里的梯度下降法和LSE还可以换成其他的优化算法

模糊关系

模糊关系矩阵

模糊关系矩阵的求法

多层模糊关系矩阵压缩

试想一下，已知“逆天”和“玩原神”之间存在一层模糊关系1，“玩原神”和“米孝子”之间存在一层模糊关系2。那么是否可以将关系1和关系2合起来表达，使得可以通过输入“逆天”的成分推断“米孝子”的成分？

这样合二为一的矩阵被称为模糊关系矩阵。在没有模糊关系矩阵时，“逆天”作为输入，需要先和模糊关系1进行模糊推理，得到输出1，再将输出1输入到模糊关系2，得到最终输出。而有了模糊关系矩阵，直接将“逆天”输入模糊关系矩阵，即可得到最终输出。

模糊关系矩阵压缩的操作类似于矩阵乘法，只不过原本的乘和加的操作变成了模糊集逻辑操作。在max-min规则中，就是将矩阵乘法的乘号换成min，加号换成max。在max-product规则中，乘号不变，加号换成max。举个例子：

现有模糊关系矩阵A和B，如下：

模糊拓展定理

模糊四则运算