滤波器基本参数

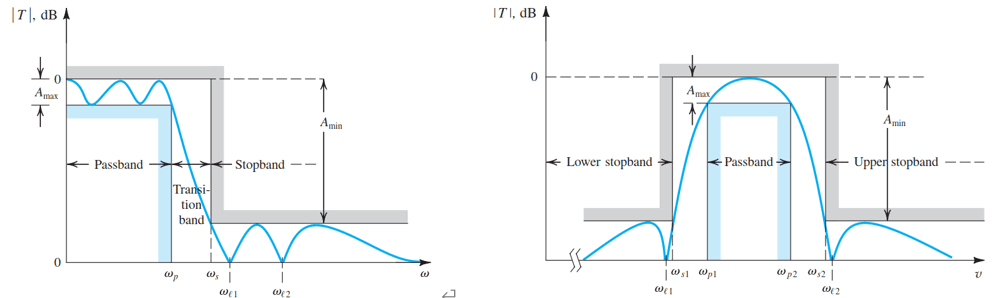
上图展示了滤波器通带、阻带、过渡带。

特征角频率和特征频率($f_0/f_n$) pole frequency/ nature frequency

它只与滤波用的电阻和电容元件的参数有关，通常对于带通(带阻）滤波器，称为带通(带阻）滤波器的中心角频率或中心频率$f_0$，是通带(阻带）内电压增益最大(最小）点的频率。

滤波器的截止频率（$f_c$）cut-off frequency

一般地是指幅度响应比通带低3 dB时的频率。无论是什么样的滤波器，截止频率一般都是指-3db的位置，也就是说从滤波器的通带的增益算起，下降-3db的位置。

Chenqiao原话：但是一些文献里面认为$f_0$就是截止频率$ f_c $，截止频率不一定需要在-3dB point。这里需要根据实际情况讨论。

无源滤波器(Passive Filter)

电容、电抗和阻抗的关系：

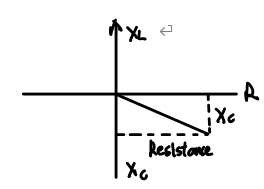
所有滤波器的公式都是将电容和电抗表现成阻抗的形式，代入电路得出的。

一阶无源滤波器

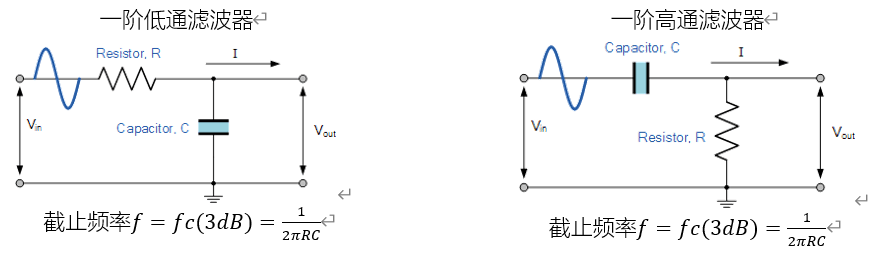
低通:

一阶低通滤波器：输出的电压等于夸在电容两端的电压，输出信号的相位

$\psi=\phi_0-arctan⁡(R/X_C )=\phi_0-arctan⁡(2πfRC)。$

因此，当到达截止频率$X_C=R$时，相位移动为-45°

高通：

输出的电压等于夸在电阻两端的电压，相位：

$\psi=\phi_0+π/2-arctan⁡(2πfRC)$

因此，当到达截止频率$X_C=R$时，相位移动为+45°

二阶滤波器

对于高阶滤波器，可以看成多个一阶串联，因此相位移动是叠加的。例如二阶高通滤波器截止频率的相位移动就是+90°

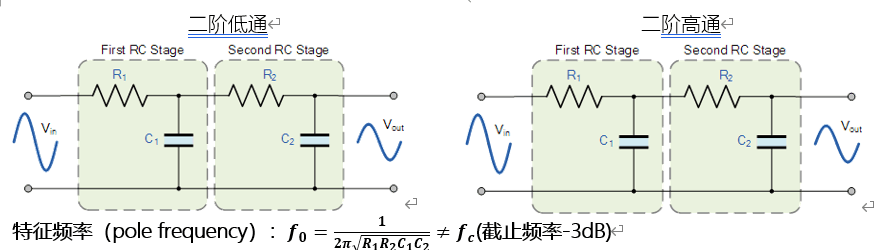
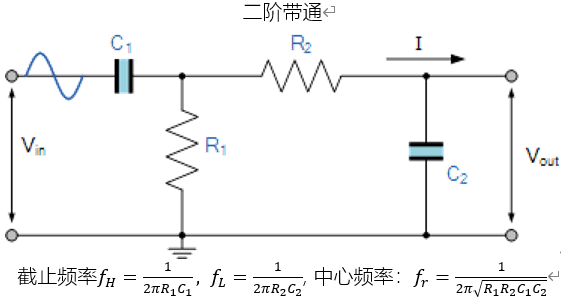
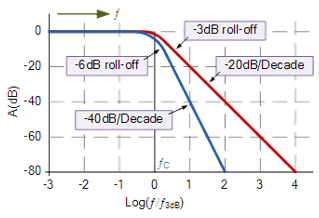
增益下降slope比较

二阶滤波器可以看做两个一阶滤波器串联。因此假设对于某一频率，一个二阶滤波器由两个同样的一阶滤波器串联而成。一阶滤波器的slope=-20dB/Decade, 那么二阶滤波器slope就是一阶滤波器的平方也就是-40dB/ Decade. (Decade=f/fc(3dB))

对于二阶带通滤波器而言，两端的slope是两个独立的一阶滤波器，因此还是-20dB/ Decade.

有源滤波器(Active Filter)

有源滤波器带有运放，因此可以实现增益大于1（0dB）。且提供更好的输入输出阻抗。

有源低通滤波器

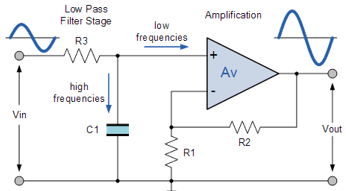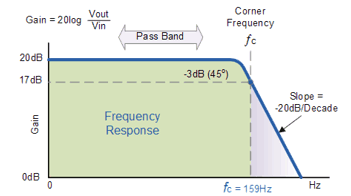其截止频率$f=1/2πRC$,

增益$DC Gain=(1+R_2/R_1 )$,

如果把低通滤波器的电阻放在反馈电阻上，同样能通过影响不同频率的放大倍数进行滤波。这样可以得到更好的输入阻抗。

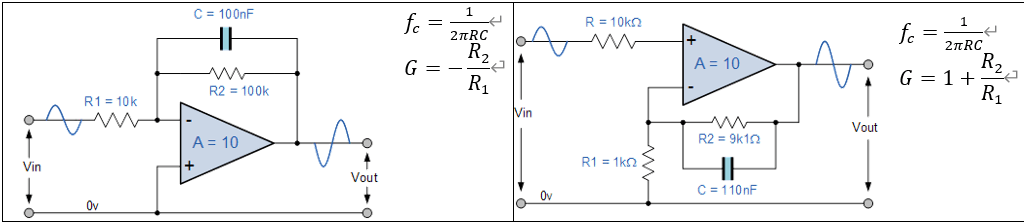
一阶有源HPF只需要把电容更换位置，放在信号输入端即可（也就是R1前面）。

有源高通滤波器(二阶)

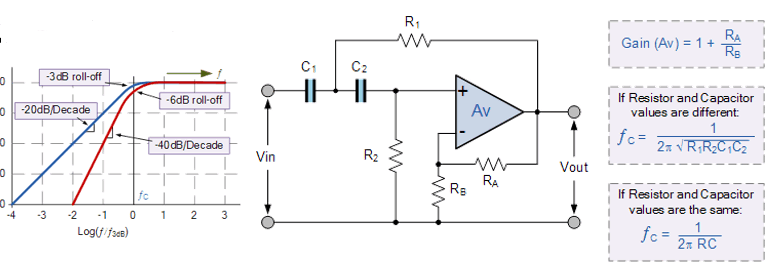
同无源滤波器分析的一样，有源一阶滤波器的slope斜率为-20dB/Decade, 二阶为-40dB/Decade.

有源带通滤波器(二阶)

有源带阻滤波器

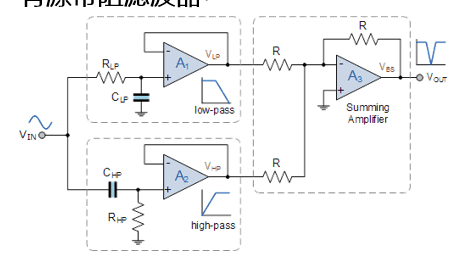
相当于是一个有源加法器，输入信号为一个高通的输出和一个低通的输出。增益-频率响应为高通和低通的叠加。
有源的二阶带通和带阻中心频率计算公式都是

$f_0=\sqrt{(f_L⋅f_H)}$

陷波滤波器(Notch Filter) 是带阻滤波器的一种，只不过阻带很窄。（好像不是重点，没考过）

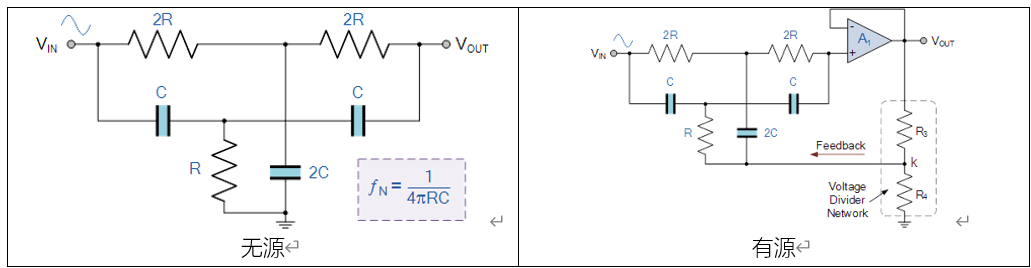
Sallen-Key 滤波器（五星级）

Sallen-key是设计有源滤波器设计的一种拓扑结构，VCVS（Voltage-controlled voltage-source）滤波器的变种，由麻省理工学院林肯实验室的R. P. Sallen and E. L. Key 在1955所提出。

Q Factor

用频率定义Q：电路发生谐振的频率 ω0 称为谐振频率谐振峰两边 I ＝（1/2） Im 处的频率值ω2j 和 ω1j 之间宽度定义为通频带宽度 BW，衡量一个谐振器在电路中性能的好坏。常用品质因数 Q ＝ ω0/ω2j －ω1j 来描述，Q 的物理意义是在谐振频率ω0 附近将具有更强的尖峰；对于离 ω0 较远的频率，则影响很弱或不影响。

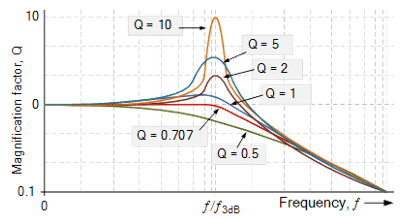
对低通和高通滤波器而言,Q值等于滤波器电路电压增益（截止频率对应处的增益）模$|A_u |$与通带增益的模之比 $|A_{up}|$；对带通(带阻）滤波器而言，Q值等于中心角频率与通带(阻带）宽度bw之比。

S-K滤波器的整体模型

图中电阻根据低通、带通、高通不同要求替换成电容。

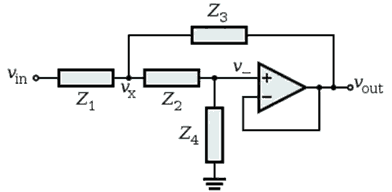
计算通式为：

$\frac{V_{out}}{V_{in}}=\frac{Z_3\times Z_4}{Z_1\times Z_2 + Z_2\times Z_3 +Z_3 \times Z_4 +Z_1 \times Z_3}$

S-K低通&高通滤波器

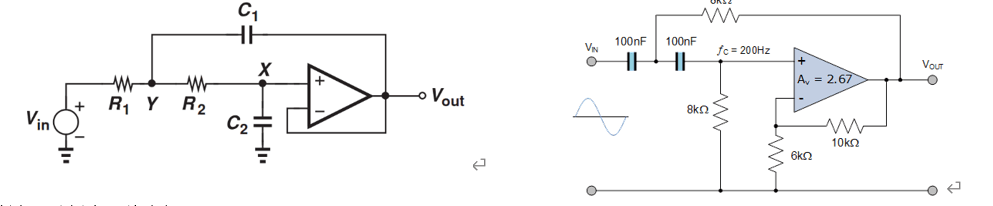
以低通滤波器为例：

$Z_1=R_1,Z_2=R_2,Z_3=\frac{1}{(sC_1 )},Z_4=\frac{1}{(sC_2 )}, 其中 s=jω$ $A=\frac{\frac{1}{sC_1}\times \frac{1}{sC_2}}{R_1R_2+R_2\frac{1}{sC_1}+\frac{1}{sC_1}\times \frac{1}{sC_2}+R_1\frac{1}{sC_1}}$ $= \frac {1}{R_ {1}R_ {2}C_ {1}C_ {2}s^ {2}+R_ {2}C_ {2}s+1+R_ {1}C_ {2}s}$ $= \frac {1}{R_ {1}R_ {2}C_ {1}C_ {2}s^ {2}+C_ {2}s(R_ {1}+R_ {2})+1}$

特征频率:

（有时候认为$f_n=f_c$，$f_c$不在-3dB点，所以截止频率也是这个，具体要看题目）

$f_n=\frac{1}{(2\pi\sqrt{(R_1 R_2 C_1 C_2 )}}$

品质因子Q：

$Q=\frac{1}{R_1+R_2}(\sqrt{R_1 R_2 \frac{C_1}{C_2} })$

当$R_1=R_2, C_1=C_2$ 时，Q 有：

$Q=\frac{1}{3-A}$

其中A为放大电路的放大倍数。

设计S-K滤波器的例题

设计一个具有以下特性的二阶高通Sallen-Key滤波器电路：$f_C=200Hz，Q=3$。

解：

为简化计算，认为$R_1=R_2,C_1=C_2$

$f_c=1/2πRC=200Hz$, 选择c=100nF继续计算， R=7957Ω。（这道题认为$f_c=f_0$，PPT上举例原题）

$Q=3=\frac{1}{3-A},A=\frac{3Q-1}{Q}=2.667$

所以放大电阻分别取10K和6K

设计S-K滤波器生成类型的判定：

滤波器的类型是看 $\omega_0$ 处有没有bump来判定的，因此使用品质因素Q来判定

巴特沃夫滤波器没有bump,因此Q<1 贝塞尔滤波器Q≈1 切比雪夫滤波器Q>1