Control Systems Part1-1-控制系统概述及其基本分析

控制系统概述

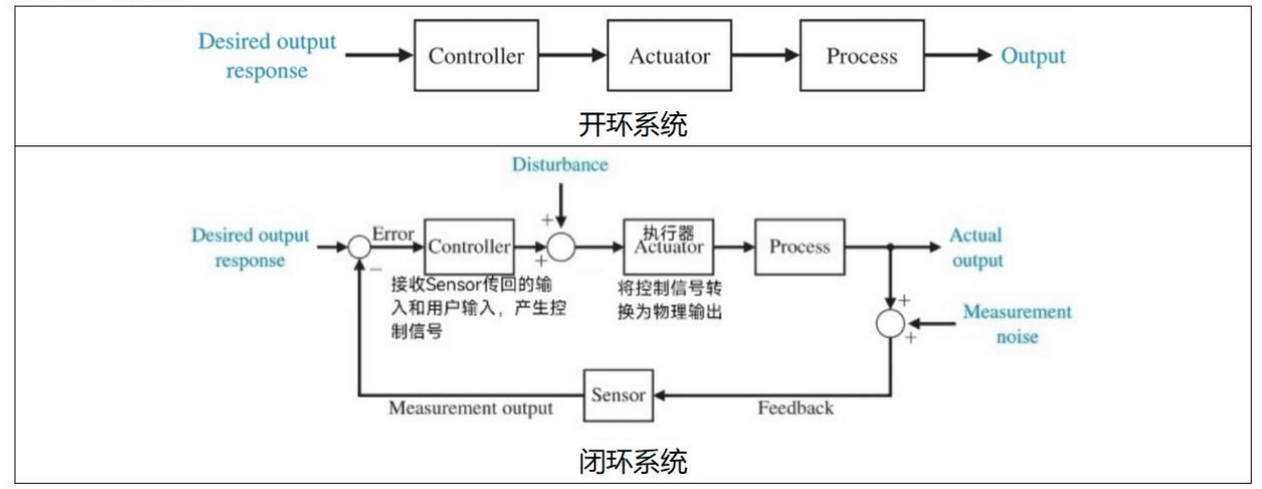
如上图所示，根据有无feedback，控制系统被分为开环控制系统和闭环控制系统两类。在一个抽象出的系统中，使用Sensor取回需要的数据，Controller处理数据并转换为控制信号，Actuator收到控制信号后将其转化为物理上的输出

这一门课仅涉及闭环线性时不变控制系统

开环控制系统

开环控制系统因为没有反馈的存在，因此系统的精度取决于校准的程度。

而且，开环控制系统无法消除收到的干扰或运行变化所造成的影响。

闭环控制系统

闭环控制系统将它现在的实际输出与期望的输出进行对比，再进行控制。这个过程被称为反馈。

通常来说，使用负反馈来控制一个系统。（i.e., 将系统期望的输出-现在的输出，得到error值）。在这门课中，只学习负反馈的情况。

对系统进行建模（引入）

使用拉普拉斯变换表达系统传输函数

一个带有反馈的系统，其系统可以用一个差分方程来描述。通式是：

$$\frac {d^ {n}y}{dt^ {n}} + a_ {n-1} \frac {d^ {n-1}y}{dt^ {n}1} + a_ {1} \frac {dy}{dt} + a_ {0} y(t)= b_ {m} \frac {d^ {m}x}{dt^ {m}} + b_ {1} \frac {dx}{dt} + b_ {0} x(t)$$

通过变换将$y(t)$移动到一边之后，可以得到带有$x(t)$的和不带$x(t)$的两部分。带有$x(t)$的部分构成了系统的强迫响应（即，由外部激励引起的）。没有$x(t)$的部分是系统系统的自由响应。如下图

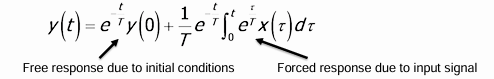
对这个系统函数进行拉普拉斯变换，$y(t)$和$x(t)$变换为$Y(s)$和$X(s)$。移项后即可传输函数$H(s)$

$$H(s)=\frac{Y(s)}{X(s)}=\frac{b_ms^m+b_{m-1}s^{m+1}+...+b_1s+b_0}{s^n+a_{n-1}s^{n-1}+...+a_1s+a_0}$$

对于这个传输函数：

• 分子称为特征多项式（Characteristic Polynomial）: 传输函数的分母
• 特征函数（Characteristic Equation）: 让传输函数分母=0
• 极点：分母=0的解
• 零点：分子=0的解

系统的各项指标

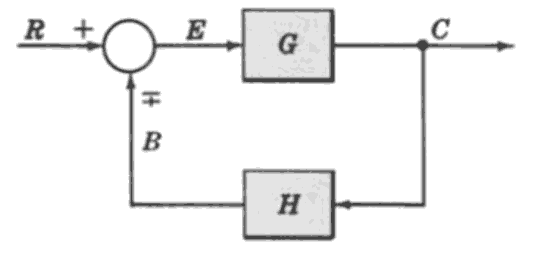
任何一个系统都可以被描述为上图的形式，其中：

• G：前向传输函数（Forward Transfer Function）
• H：反馈传输函数（Feedback Transfer Function）
• GH：开环传输函数（Open-loop transfer function）
• C/R：闭环传输函数（closed-loop transfer function）$\frac{C}{R}＝\frac{𝐺}{1±𝐺𝐻}$；对于分母，正反馈是减，负反馈是加。
• E/R：误差比（Error ratio）$\frac{𝐸}{R}＝\frac{1}{1±𝐺𝐻}$
• B/R：primary feedback ratio $\frac{𝐵}{𝑅}＝\frac{𝐺𝐻}{1±𝐺𝐻}$

开环与闭环传输函数：

对于上图所示的这个系统，其闭环传输函数为$\frac{C}{R}＝\frac{𝐺}{1±𝐺𝐻}$​，其推导很简单，以负反馈系统为例：

$$[𝑅−𝐶⋅𝐻(𝑠)]G(𝑠)=C$$ $$RG(𝑠)−CG(𝑠)H(𝑠)=C$$ $$RG=C[1+𝐺(𝑠)𝐻(𝑠)]$$ $$\frac{𝐶}{𝑅}=\frac{𝐺}{1+𝐺𝐻}$$

研究闭环传递函数的原因很好理解：C(s)=R(s)H(s)，可以轻易通过闭环传输函数得到系统输出

那什么是开环传递函数呢？其定义是：断开系统的主反馈通路，则前向通路传递函数$G(s)$与反馈通路传递函数$H(s)$的乘积称为系统的开环传递函数。因此，该系统的开环传递函数就是$GH(s)$

为什么需要开环传递函数呢？开环传递函数虽然没有直接的物理意义，但是其却包含了系统内所有的传输函数，因此可以从数学层面通过开环传递函数对系统的零极点、稳定性进行研究，且相较于闭环传递函数，减少了计算量。

开环传递函数是针对于闭环系统而言的，而不是指开环系统的传递函数

二阶系统传输函数的构成

对于任意一个二阶系统，其可以表示为

$$\frac{\omega_n^2}{s^2+2\zeta\omega_ns+\omega_n^2}$$

其中：

• $\zeta$称为阻尼比(damping ratio)。
• $\omega_n$称为无阻固有频率（damped natural frequency），其物理意义是在系统没有阻尼的时候，自然振荡的频率。

对这个系统求单位阶跃响应（$u\left(t\right)\ $）：

$$L\left[u\left(t\right)\right]＝u(s)=\frac{1}{s}$$ $$C\left(s\right)=u\left(s\right)H\left(s\right)=\frac{\omega_n^2}{\left(s^2+2\zeta\omega_ns+\omega_n^2\right)s}$$

将该式因式分解后反拉普拉斯变化得到时域响应

$$C\left(s\right)=\frac{1}{s}-\frac{s+2\zeta\omega_n}{s^2+2\zeta\omega_ns+\omega_n^2}=\frac{1}{s}-\frac{s+\zeta\omega_n}{\left(s+\zeta\omega_n\right)^2+\omega_d^2}-\frac{\zeta\omega_n}{\left(s+\zeta\omega_n\right)^2+\omega_d^2}$$ $$c(t)=1-\frac{1}{1-\zeta^2}e^{-\zeta\omega_nt}sin(\omega_dt+\beta), \beta=arctan(\sqrt{1-\zeta^2}/\zeta)=arccos\zeta$$

其中$\omega_d=\omega_n{\sqrt{1-\zeta^2}}$，称为阻尼固有频率（damped natural frequency），是系统受阻时的角频率。
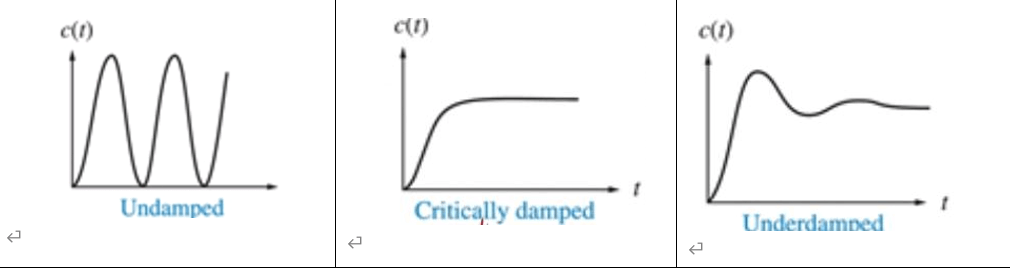
在$\zeta=0$时，称为无阻尼（undamped），系统持续振荡，系统极点位于虚轴上；
在$\zeta＝1$时，称为严阻尼（Critically damped），系统不会出现振荡，而是直接逼近稳态值，极点位于左实轴；
在$0<\zeta<1$时，称为欠阻尼（underdamped）, 系统在振荡后收敛于稳态值，极点位于s域左侧，有虚部分量。
如下面三图所示

瞬态响应的各项指标

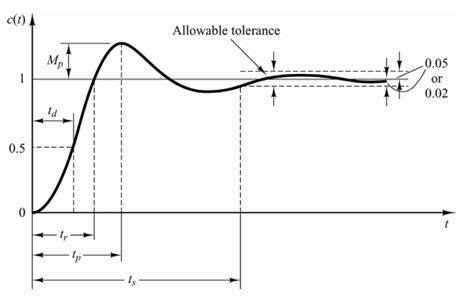
在这样的一个二阶系统响应中：

• Raise time $t_r$: 响应从10%-90% 或 0%-100% 所需的时间；

$$t_r=\frac{\pi-\beta}{\omega_d}$$

• Peak time $t_p$：响应到达最高峰值所需的时间；

$$t_p=\frac{\pi}{\omega_d}$$

• Maximum Overshoot $M_p$：$\frac{响应过冲-终值}{终值} $的比例；

$$M_p=e^{-(\sigma/\omega_d)\pi}=e^{-(\sqrt{1-\zeta^2})\pi}\times100%$$

• Settling time $t_s$：响应稳定至稳态值所需的时间，通常允许2%或5%的误差：（下式中T被称为时间常数，由瞬态响应的衰减速度决定，$T=\frac{1}{\zeta\omega_n}$。）

$$t_s=4T=\frac{4}{\zeta\omega_n}(2\% criterion); t_s=3T=\frac{3}{\zeta\omega_n}(5\% criterion)$$

系统稳态分析

基于开环传递函数的系统的分类

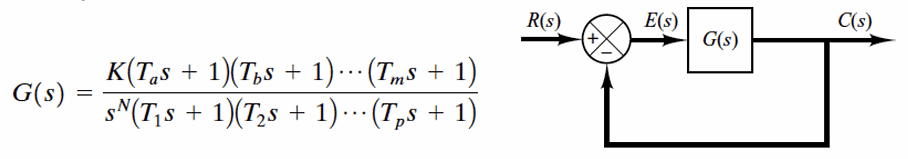
对于G(s)，如果其分母有单独的$s^N$，N为几它就是type N系统。例如没有单独的s只有（Ts+1），那就是type0系统；有s(Ts+1)，就是type1系统

注意：系统的阶数(order)是指的分母内s的最高次，这里系统的类别（type）是指的孤立s的次数

系统的稳态误差

对于一个实际的控制系统，其稳态输出不可能在任何 情况下都与输入量一致或相当，也不可能在任何形式的扰 动作用下都能准确地恢复到原平衡位置。因此控制系统的稳态误差是一项重要的技术指标。

稳态误差的定义

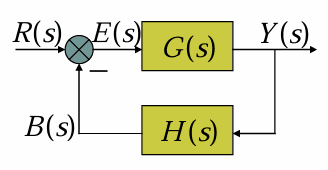
系统误差的定义：系统的输入$r(t)$和主反馈信号$b(t)$之差。

$$e(t)=r(t)-b(t)$$

稳态及误差：当时间趋于无穷时的系统误差即为稳态误差，记为$e_{ss}$

$$e_{ss}=\lim_{t\rarr\infty}e(t)$$

只有当系统稳定时，研究稳态误差才有意义。

如何求稳态误差

对于任意一个系统，其开环传递函数为G(s)H(s)，其中前向传递函数$G(s)$:

$$G(s)=\frac{K(T_as+1)(T_bs+1...(T_ms+1))}{(T_1s+1)(T_2s+1)...(T_ps+1)}$$

闭环传递函数是输出比输入得到的，因此有

$$\frac{G(s)H(s)}{1+G(s)H(s)}=\frac{Y(s)}{R(s)}$$ $$Y(s)=\frac{G(s)H(s)}{1+G(s)H(s)}R(s)$$

根据上图，$B(s)$有：

$$B(s)=Y(s)H(s)$$

而$E(s)$恰好等于$R(s)-B(s)$，因此：

$$E(s)=R(s)-Y(s)H(s)=R(s)-\frac{G(s)H(s)}{1+G(s)H(s)}R(s)=R(s)\bigg[\frac{1+G(s)H(s)-G(s)H(s)}{1+G(s)H(s)}\bigg]$$ $$=R(s)\frac{1}{1+G(s)H(s)}$$

而前面小节介绍的误差比就是:

$$\frac{E(s)}{R(s)}=\frac{1}{1+G(s)H(s)}$$

现在已经有了$E(s)$的表达式，由终值定理，$\lim_{s\rightarrow0}sF(s)=\lim_{t\rightarrow\infty}f(t)$，也就是系统稳定的情况。因此：

$$e_{ss}=\lim_{t\rarr\infty}e(t)=\lim_{s\rarr0}sE(s)=\lim_{s\rarr0}s\frac{1}{1+G(s)H(s)}R(s)$$

只有稳定的系统，才可计算稳态误差。

不同type系统的稳态误差

为了更直观地简便举例解释，现考虑H(s)为1，即单位负反馈的情况。此时$G(s)H(s)=G(s)$，那么$\frac{1}{1+G(s)H(s)}R(s)$可以作如下推导：

$$G(s)=\frac{K(T_as+1)(T_bs+1...(T_ms+1))}{(T_1s+1)(T_2s+1)...(T_ps+1)}$$ $$\frac{1}{1+G(s)H(s)}R(s)=\frac{1}{1+\frac{K(T_as+1)(T_bs+1...(T_ms+1))}{(T_1s+1)(T_2s+1)...(T_ps+1)}}R(s)$$ $$=\frac{(T_1s+1)(T_2s+1)...(T_ps+1)}{(T_1s+1)(T_2s+1)...(T_ps+1)+K(T_as+1)(T_bs+1...(T_ms+1)){}}R(s)$$

也就是，这个式子变成了：（这个式子后面作为辅助解释）

$$\frac{G(s)分母}{G(s)分母+G(s)分子}R(s)$$

unit step 输入下

输入信号u(t)的$U(s)=\frac{1}{s}$。此时：

$$\lim_{s\rarr0}sE(s)=\lim_{s\rarr0}s\frac{1}{1+G(s)H(s)}R(s)=\lim_{s\rarr0}sE(s)=\lim_{s\rarr0}\frac{1}{1+G(s)H(s)}$$

记单位阶跃输入下的静止位置误差常数 （static position error constant）是$K_p$，等于开环传递函数$G(s)H(s)$的极限:

$$K_p=\lim_{s\rarr0}{G(s)H(s)}$$

那么$e_{ss}$就可以由如下式子求到：

$$e_{ss}=\frac{1}{1+K_p}(仅unit\ step输入适用)$$

同时我们发现，对于G(s)没有孤立s在分母的函数（即type0系统），$e_{ss}=\frac{1}{1+K_p}$适用。但是一旦G(s)的分母存在孤立s，那么$K_p=G(0)=\infty$，$e_{ss}=0$；

这一点通过上面推出的$\frac{G(s)分母}{G(s)分母+G(s)分子}R(s)$也很好解释，G(s)分母存在s，且$s\rightarrow0$，因此$e_{ss}=0$

因此，对于系统输入单位阶跃响应，稳态误差有：

• type0系统的$e_{ss}=\frac{1}{1+K_p}$
• type1或更高type系统$e_{ss}=0$，$K_p=\lim_{s\rightarrow0}{G(s)H(s)}$

unit ramp 输入下

输入信号$r(t)$的$R(s)=\frac{1}{s^2}$，此时：

$$\lim_{s\rarr0}sE(s)=\lim_{s\rarr0}s\frac{1}{1+G(s)H(s)}R(s)=\lim_{s\rarr0}sE(s)=\lim_{s\rarr0}\frac{1}{s+sG(s)H(s)}$$

因此$s\rightarrow0$，分母$s+sG(s)H(s)$前面孤立的s可以直接当0对待，因此分母只剩下$sG(s)H(s)$

记单位斜坡输入下静止速度误差常数 （static velocity error constant）是$K_v$，等于$sG(s)H(s)$的极限:

$$K_v=\lim_{s\rarr0}{sG(s)H(s)}$$

此时$e_{ss}$

$$e_{ss}=\frac{1}{K_v}$$

当G(s)分母没有孤立s（即，type0系统时），$K_v=sG(0)=0$

$$e_{ss}=\frac{1}{K_v}=\infty$$

使用$\frac{G(s)分母}{G(s)分母+G(s)分子}R(s)$也很好解释，$R(s)=\frac{1}{s^2}$，$G(s)分母$未能对其引入的s进行消除，分母带趋近于0的s，因此$e_{ss}=\infty$

同理可得，当type1系统时，$e_{ss}=\frac{1}{K_v}$，type2及以上系统$e_{ss}=0$

因此，对于系统输入单位斜坡响应，稳态误差有：

• type0系统$e_{ss}=\infty$
• type1系统$e_{ss}=\frac{1}{K_v},K_v=\lim_{s\rightarrow0}{sG(s)H(s)}$
• type2或更高type系统$e_{ss}=0$

PPT还介绍了unit-parapolic input和它的$K_a$推导思路和前面一致。后面没怎么用，这里就省略了

总览

劳斯-赫尔维茨（Routh–Hurwitz）稳定性准则

参考视频：YouTube-Brian Douglas

Routh-Hurwitz 稳定性准则是对控制系统稳定性的一种数学检验，是线性时间不变 （LTI） 控制系统稳定性的必要和充分条件。

在信号与系统中学过，系统特征方程（传输函数的分母=0）解出来的特征根有：

• 完全在左半平面时，系统stable
• 在虚轴上时，系统critical stable（保持频率振幅不变的震荡）
• 出现在右半平面时，系统unstable

在系统阶数较少时，我们可以利用因式分解将分母拆开，来求得极点。也可以很轻易地用部分分式展开法来求逆变换，观察其时域区域在$t\rightarrow\infty$是否收敛。

$$H(s)=\frac{1}{s+1}\frac{1}{s-2}\frac{1}{s+3}=\frac{A}{s+1}+\frac{B}{s-2}+\frac{C}{s+3}$$

但是，当遇到阶数非常非常高的系统时怎么办呢？有没有什么办法无需进行因式分解，就可以看出有没有极点出现在右半平面的方法？这就是Routh-Hurwitz 稳定性判据在干的事儿。

Routh-Hurwitz判据

引入

如果一个特征方程里面的所有项，有一项出现了与其他不同的符号，例如下面这个

$$s^4+3s^3-5s^2+s+2$$

此时可以立马判定这个系统是不稳定的，因为它一定会拆分出一个$(s-C)$(C是任意正常数项)的项目，来凑这个负号。

但是当符号全部相同时，就无法判定了。因为这种情况下可能会节出来实部为正，含有虚数的特征根。（无论是正负号，若全负号可以把它提一个-1出来放在传输函数分子，变成正号）。例如下面这个例子

$$G(s)=\frac{1}{s^4+2s^3+3s^2+10s+8}=\frac{1}{s^2-s+4}\frac{1}{s+2}\frac{1}{s+1}$$ $$roots:0.5\pm j\sqrt{3.75};\ -2;\ -1$$

因此我们必须使用其他更复杂的代数手段来判定，简单地观察符号是行不通的。

Routh 矩阵

Routh矩阵定义了一种填写矩阵的方法，可以通过观察矩阵的第一列来看出是否有右半平面的根

首先，假设特征函数是：

$$D(s)=As^6+Bs^5+Cs^4+Ds^3+Es^2+Fs^1+Gs^0$$

因为特征函数有6阶，因此有7列。

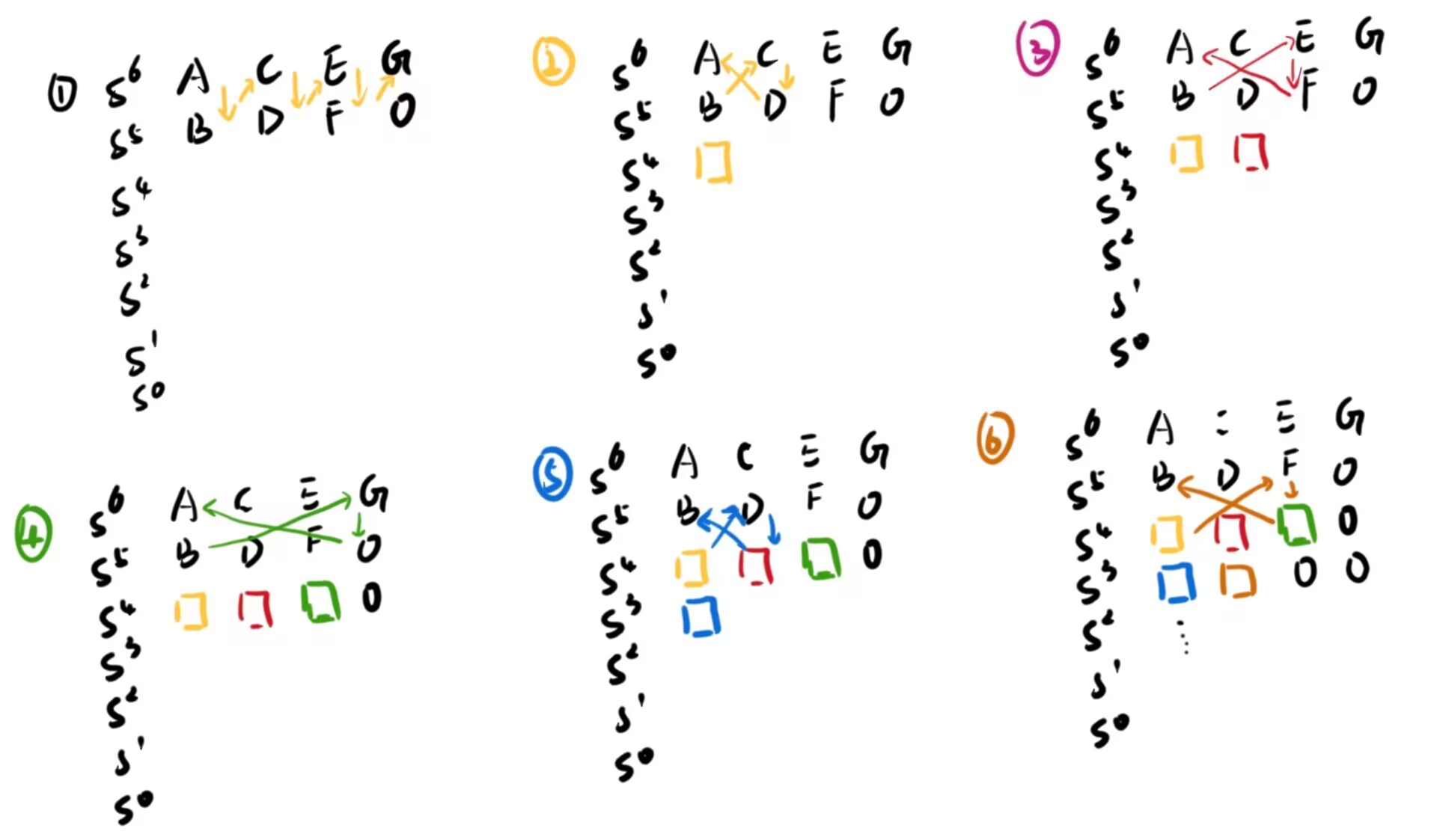
1. 首先将ABCDEFG按照上图第一步填入矩阵
2. 使用$\frac{BC-DA}{B}$算出黄色格子，如上图第二步
3. 使用$\frac{BE-FA}{B}$算出红色格子，如上图第三步
4. 使用$\frac{BG-0\times A}{B}$算出绿色格子，如上图第四步；此时到达了末尾，因此绿色格子后面填0，换行
5. 使用$\frac{黄\times D-红\times B}{黄}$算出蓝色格子，如上图第五步
6. 使用$\frac{黄\times F-绿\times B}{黄}$算出棕色格子，如上图第六步；此时棕色格子后面，绿色格子下面按照这个规则算出来等于0，因此换行；
7. 保持这个规则，一直算到全部为0的一行，舍弃掉该行，剩下的就是Routh矩阵

通式可以写为：

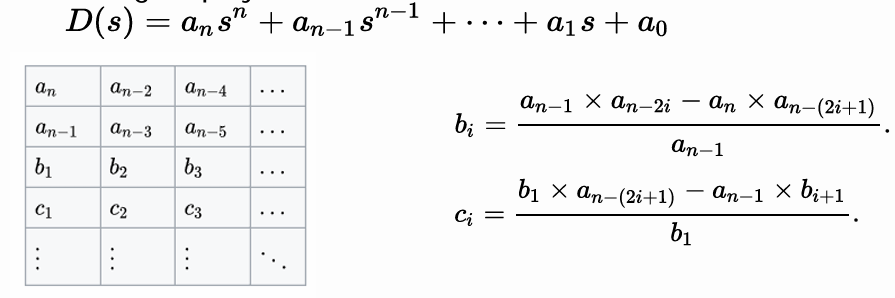
稳定性判定

• 当Routh矩阵的第一列全部是正数时，系统稳定
• Routh矩阵的第一列有几次符号变化，就有几个右边平面的根

举个例子

沿用前面例子的系统传输函数：

$$G(s)=\frac{1}{s^4+2s^3+3s^2+10s+8}=\frac{1}{s^2-s+4}\frac{1}{s+2}\frac{1}{s+1}$$ $$roots:0.5\pm j\sqrt{3.75};\ -2;\ -1$$

首先，转写为Routh矩阵，上式特征方程为$s^4+2s^3+3s^2+10s+8$。按照下图展示的步骤进行转写

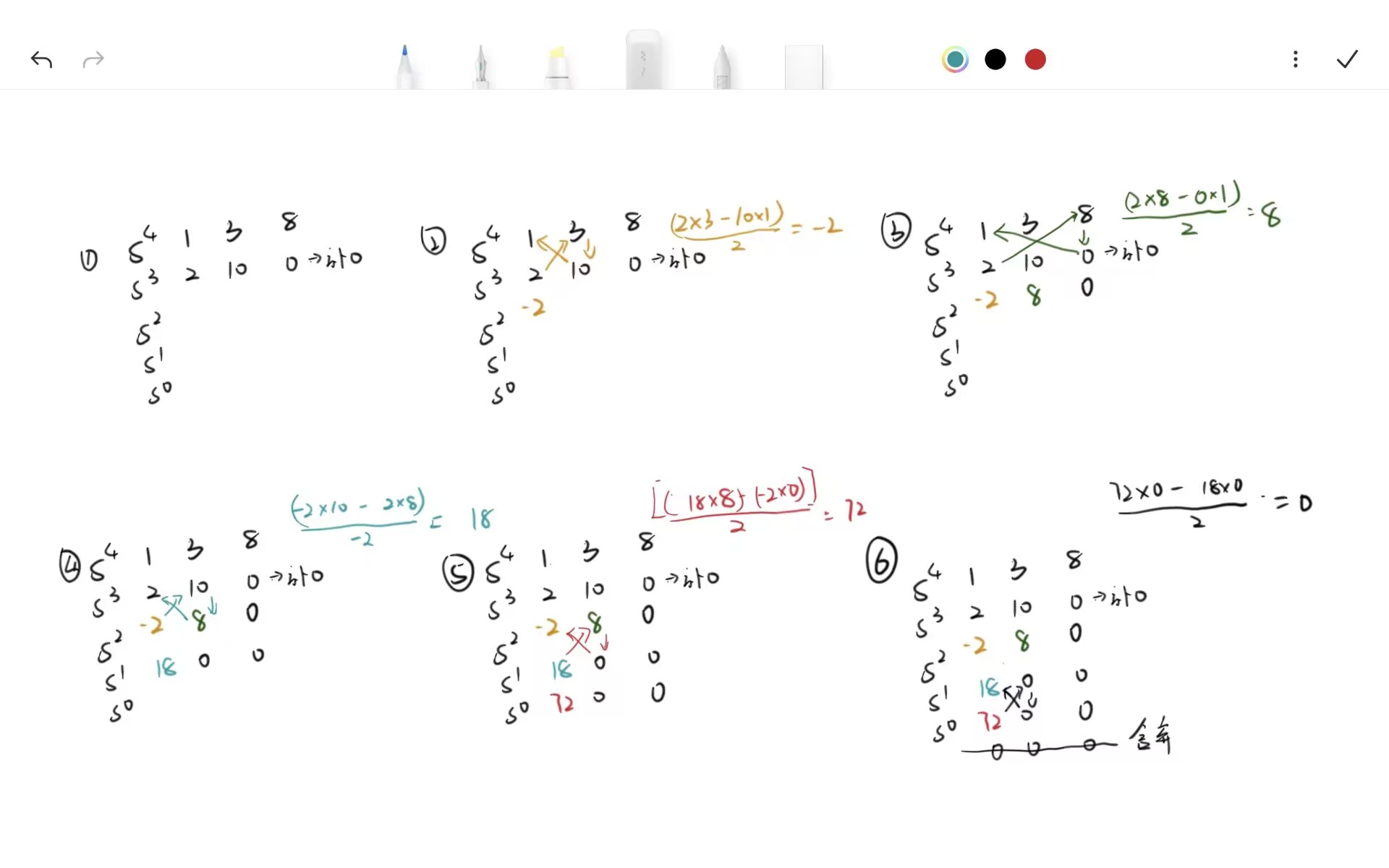
在Routh矩阵中，第一列经历了从2到-2 和 从-2到18 两次符号变换。因此：系统不稳定，有两个位于右侧的根