Control-Systems-Part2-Lectrue4-根轨迹

引入

我们在研究系统极点的路径时，都是对闭环传递函数而言的。因为闭环传递函数的零极点可以直接反应系统的一些特性，例如稳定性，收敛速度，是否存在过冲等等。

考虑下图这样的一个系统，其系统闭环传递函数为$\frac{KG(s)}{1+KG(s)H(s)}$。我们研究的就是$1+KG(s)H(s)=0$时产生的极点。但是，我们的分析对象其实是$G(s)H(s)$这个开环传递函数，我们是通过分析OLTF，来研究CLTF的根。

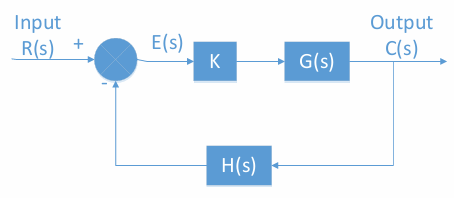
而所谓根轨迹，就是随着增益K的变换，CLTF极点的移动路径。而这个轨迹可以通过CLTF，即$G(s)H(s)$的极点和零点绘制出来。

根轨迹的基本特性

Dr.Huda PPT上的规则比较基础，但下一章会用到超出这个范围外的知识。这个视频讲了更普适的规则【自动控制原理】8_根轨迹_Part2_根轨迹手绘技巧_哔哩哔哩_bilibili。下面的笔记是结合二者写的

根轨迹的数种规则

规则1：系统的根轨迹条数等于系统极点个数或零点个数（取最大的那个）

例如$G(s)=\frac{(s+4)(s+1)}{(s+3)(s+0.5)}$，系统有2个零点2个极点，Max(2,2)=2，因此系统有两条根轨迹

规则2：根轨迹总是从OLTF的极点移动到OLTF的零点

我们先来研究一下系统的特征方程。为了简化举例，这里考虑单位反馈系统，其传递函数是：

$$\frac{1}{1+KG(s)}$$

其特征方程是：

$$1+KG(s)=0$$

其中，$G(s)$称为Loop gain（$KG(s)$才是OLTF），其可以拆分为分子和分母部分：$G(s)=\frac{M(s)}{D(s)}$，特征方程为

$$1+K\frac{M(s)}{D(s)}=0$$

改写一下就是：

$$D(s)+KN(s)=0$$

前面提到，根轨迹是$K=0\to\infty$。当$K=0$时，特征方程的是$D(s)=0$，因此是OLTF的极点；当$K=\infty$时，特征方程是$N(s)=0$，因此是OLTF的零点。

规则3：实轴上的根轨迹存在于从右向左数，OLTF的奇数个极点或零点的左侧。

如下图所示。需要注意的是，只在实轴上有这个规则。

规则4：如果复数根存在，则其一定是共轭的，即沿着实轴对称

规则5：若极点和零点的个数不足以让它们成对，则会孤立的根轨迹会指向无穷或从无穷来

• 对极点而言，它将指向无穷。如下图

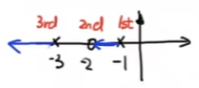
• 对零点而言，将从无穷指向它。如下图

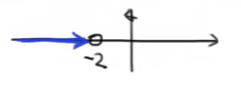
规则6：根轨迹沿渐近线移动。渐近线求法如下

记极点个数为n，零点个数为m。渐近线与实轴的交点是：

$$\sigma=\frac{极点的和-零点的和}{n-m}$$

渐近线与实轴的夹角是：

$$\theta=\frac{2q+1}{n-m}\pi,q=0,1,...,n-m-1$$

举个例子：对于$\frac{1}{(s+1)(s+2)}$

$$\sigma=\frac{-1-2+0}{2}=-1.5$$ $$\theta_1=\frac{1}{2}\pi,\theta_2=\frac{3}{2}\pi$$

如下图

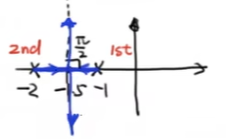
规则7：两条根轨迹永不相交

规则8：如果至少有两条根轨迹指向无穷，则所有根的合是一个常数

汇总：

• 规则1：系统的根轨迹条数等于系统极点个数或零点个数（取最大的那个）

• 规则2：根轨迹总是从OLTF的极点移动到OLTF的零点

• 规则3：实轴上的根轨迹存在于从右向左数，OLTF的奇数个极点或零点的左侧。

• 规则4：如果复数根存在，则其一定是共轭的，即沿着实轴对称

• 规则5：若极点和零点的个数不足以让它们成对，则会孤立的根轨迹会指向无穷或从无穷来（极点无穷去，零点无穷来）

• 规则6：根轨迹沿渐近线移动，渐近线与实轴交点：$\sigma=\frac{极点的和-零点的和}{n-m}$，与实轴角度：$\theta=\frac{2q+1}{n-m}\pi,q=0,1,…,n-m-1$。（其中n为极点个数，m为零点个数）

• 规则7：两条根轨迹永不相交

• 规则8：如果至少有两条根轨迹指向无穷，则所有根的合是一个常数

从特征函数的角度理解根

这里的东西会在下一章设计补偿器用到

特征方程对OLTF提出的要求

回看特征方程：

$$1+KG(z)=0$$

$KG(z)$为系统OLTF，如果将其记为$F(Z)$，则有：

$$1+F(z)=0,F(z)=-1$$

这就要求复数$F(z)$满足：

$$|F(z)|=1$$ $$\angle F(z)=\pm180^\circ(2k+1),k=0,1,2,...$$

$F(z)$的模长和角度

对于任意的$F(z)$，其可以被拆分为多个复数相乘，例如如下例子

$$F(z)=\frac{a_3+ib_3}{(a_1+ib_1)(a_2+ib_2)}=\frac{r_3\angle\theta_3}{r_1\angle\theta_1r_2\angle\theta_2}$$

此时$|F(z)|$和$\angle F(z)$可以表示为：

$$|F(z)|=\frac{r_3}{r_2r_1}$$ $$\angle F(z)=\angle(\theta_3-\theta_1-\theta_2)$$

Breakaway 和 Breakin ponit 的计算

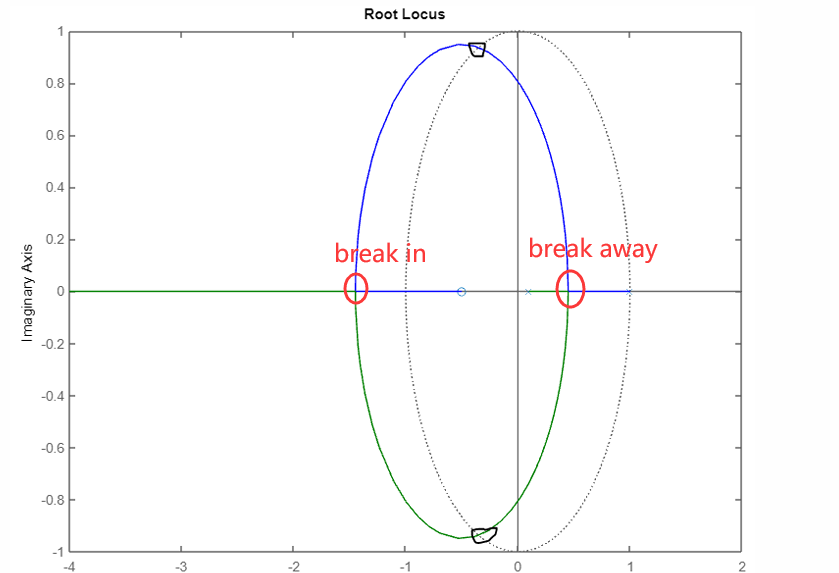
根轨迹相离的地方叫做Breakaway Point, 重新相交的地方叫做Breakin Point。如下图所示

如果将OLTF$F(z)$拆分为分子分母的形式，特征方程可以写为：

$$1+\frac{KN(z)}{D(z)}=0$$ $$K=-\frac{D(z)}{N(z)}$$

对k求导：($上导下不导-下导上不不导/分母^2$)

$$\frac{dK}{dz}=-\frac{D'(z)N-N'(z)D(z)}{N^2(z)}$$

让$-\frac{D’(z)N-N’(z)D(z)}{N^2(z)}=0$，解出来的z就是breakout 和 breakin point

举个例子，对于系统函数$G(z)=\frac{(z+0.5)}{(z-1)(z-0.1)}$

$$K=-\frac{(z-1)(z-0.1)}{(z+0.5)}$$ $$\frac{dK}{dz}=-\frac{[(z-1)+(z-0.1)](z+0.5)-(z-1)(z-0.1)}{(z+0.5)^2}=-\frac{z^2+z-0.65}{(z+0.5)^2}$$

令$-\frac{z^2+z-0.65}{(z+0.5)^2}=0$，即$z^2+z-0.65=0$，解出来$z_1=0.4487,z_2=-1.4487$。由于原loop gain的极点分别在1和0.1，而零点在-0.5，因此靠左的$z_2$是Break in point，$z_1$是Break out。它对应的图像就是这一小节开头的那张图。

从根的角度研究采样周期T对系统的影响

T对系统稳定性的影响

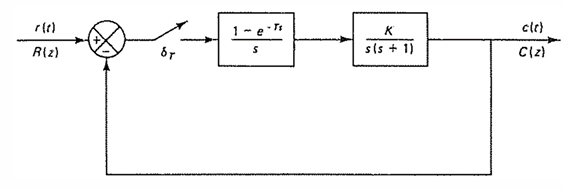
考虑下图含ZOH的系统

$$G_{ZA}(z)=(\frac{z-1}{z})Z[\frac{G(s)}{s}]=(\frac{z-1}{z})Z[\frac{K}{s^2(s+1)}]$$ $$=K(\frac{z-1}{z})Z[\frac{1}{s^2}-\frac{1}{s(s+1)}]=K\bigg(\frac{z-1}{z}\bigg)\bigg(T\frac{z}{(z-1)^2}-\frac{z(1-e^{-T})}{(z-1)(z-e^{-T})}\bigg)$$ $$=K\frac{z(T-1+e^{-T})-Te^{-T}+1-e^{-T}}{(z-1)(z-e^{-T})}$$

• T=1s时，解出poles:1，0.3678；zeros：-0.7181
• T=2s时，解出poles:1，0.1353；zeros：0
• T=2s时，解出poles:1，0.0183；zeros：0.301

分别代入三个T，使用$\frac{dK}{dz}=-\frac{D’(z)N-N’(z)D(z)}{N^2(z)}=0$解出三个T下的break in 和 Break out point。画出根轨迹，如下：

可以看到，T=1时根轨迹出单位圆的K=2.3925；T=2时出单位圆的K=1.4557；T=4时出单位圆的K=0.9653。因此，采样周期大，系统稳定性越差。

经验法则是：

• 如果闭环系统欠阻尼，则单位震荡周期内进行 8 到 10 次采样。
• 如果闭环系统过阻尼，在阶跃响应的上升时间内采样 8 到 10 次

T对系统瞬态响应的影响

我们在前面介绍过，在z域下，根越靠近$\pm 180^\circ$，单位阶跃响应的震荡频率越；根越靠近单位圆，瞬态响应收敛越慢。

观察下图的根轨迹，对于更大的T，break in point会来得更快，走出单位圆的K也会更小，即根会越快到180度，同时收敛也更慢。体现在瞬态响应上就如下图

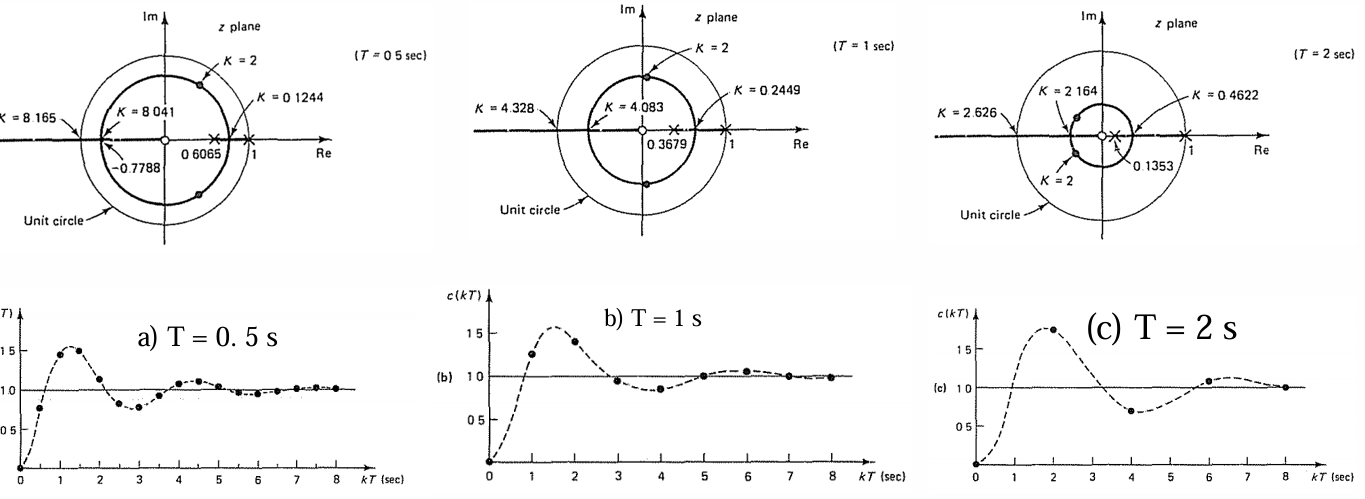
T对系统稳态误差的影响

考虑下图系统

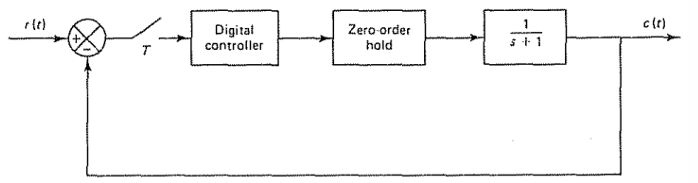
$G_{ZA}$的求法前面已经演示很多，这里不再赘述。系统特征方程为：

$$1+K\frac{z}{z-1}\frac{(1-e^{-T})}{(z-e^{-T})}=0$$

考虑unit ramp input下的稳态误差$k_v$。代入前面介绍的公式：

$$K_v=\lim_{t\to1}\frac{(1-z^{-1})GH(z)}{T}$$

• T=0.5s时，$GH(z)=\frac{0.3935Kz}{(z-1(z-0.6065))}$

代入算出$K_v=4$，$e_{ss}=\frac{1}{K_v}=0.25$

• T=1s时，$GH(z)=\frac{0.6321Kz}{(z-1(z-0.3679))}$

代入算出$K_v=2$，$e_{ss}=\frac{1}{K_v}=0.5$

• T=2s时，$GH(z)=\frac{0.8647Kz}{(z-1(z-0.1353))}$

代入算出$K_v=1$，$e_{ss}=\frac{1}{K_v}=1$

由此可见，T越大，系统的稳态误差越大