Control Systems Part1-2&3-频率响应分析法:几种图像和渐进法绘制波德图
波德图 (Bode plot)
引入-什么是波德图
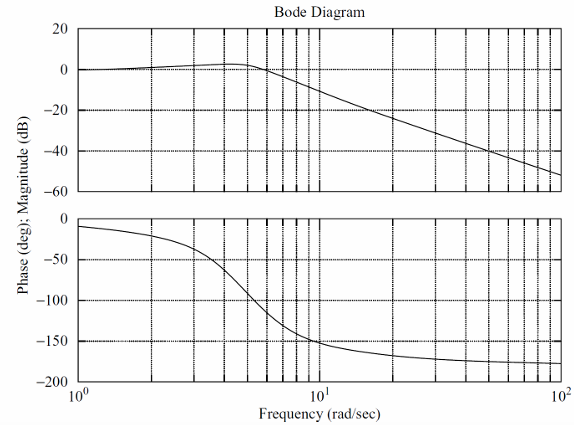
波德图是一种用于体现系统开环传输函数(open loop transfer function)频率响应的图。波德图一般是由二张图组合而成,一张幅频图(幅度通常以dB为单位),一张相频图(相位通常以degree 为单位),两图都采用对数形式的横坐标(频率轴,单位rad/sec)。下图是一个波德图的例子
采样法画波德图
幅频图
- 将$s=j\omega$代入求开环传输函数的幅频响应 $|H(s)|$(拉普拉斯变换$s=\sigma+j\omega,\ \sigma=\ 0$ 就等效于傅里叶变换了,详见信号与系统-拉普拉斯变换)
- 将其转换为对数形式($20log\left(\left|H\left(j\omega\right)\right|\right)$)
- 变化频率$\omega$计算输出得到幅频图。(注:$|H(j\omega)|$就是开环传输函数在复平面的模长,也就是$\sqrt{\left(Real^2+Img^2\right)}$)
相频图
依旧代入s=j\omega,求开环传输函数的相频响应$angle(H(j\omega))$。具体步骤如下:
- 分别求得开环传输函数的实部和虚部,将其画在复平面上
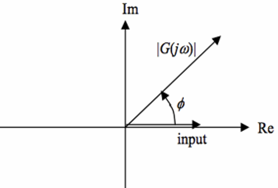
- 如果开环传输函数落在第一、四象限:$\phi=arctan\left(\frac{Im}{Re}\right)$,注意这里 Im 和 Re 不是绝对值,要带符号的!
- 如果开环传输函数落在第二象限:$\phi=\pi-arctan\left(\frac{\left|Im\right|}{\left|Re\right|}\right)$,或是$\phi=\pi+arctan\left(\frac{Im}{Re}\right)$,因为这里Im一定是正,Re一定是负,因此二式等效。
- 如果开环传输函数落在第三象限:$\phi=arctan\left(\frac{\left|Im\right|}{\left|Re\right|}\right)-\pi$
(这一部分就是复变函数里面复数角度主值的求法)
形象一点来说这个相位角就是,一二象限为正,三四象限为负,取开环传输函数向量到正半Re轴的角度。至此,得到相频图。
幅频图和相频图可以叠加在一张图上,也可以分开作图。
到这里可以发现,画幅频图和相频图需要变化$\omega$进行扫频操作。这个由人来画是非常困难的,后面会介绍更友好的渐近线画法(非常重要)。在MATLAB中,可以使用函数bode()来绘制波德图。
系统函数不同成分对幅频、相频图的影响
积分和微分
Recall——拉普拉斯变换的时域积分性质:
Recall——拉普拉斯变换的时域微分性质,若$f(t)$为因果信号,则有:
因此,我们把函数函数分母含有孤立的s称为积分器,把分子含有孤立的s称为微分器。
现在假设一个系统传输函数有一个微分器或积分器,把它分离出来,可以写成
其中$G’(s)$表示剥离和积分器或者微分器的传输函数;$s^{\pm1}$的-1和+1分别代表微分器和积分器。
(1)积分或微分对幅频图像的影响
在采样法画波德图中提到,幅频需要将其转化为$20log\left(\left|H\left(j\omega\right)\right|\right)$后计算结果。不妨将$s^{\pm1}G’(s)$代入 (这里面$s=j\omega$频率都为正),来将积分器或微分器对幅频图的影响剥离开。可以发现:
也就是说,对于积分器,其会带给幅值一个$-20log(s)$的减少;而微分器会给幅值带来$20log(s)$的增加。那么这个加减量和频率的关系是怎么样的呢?将频率代入:$20log(\omega)$
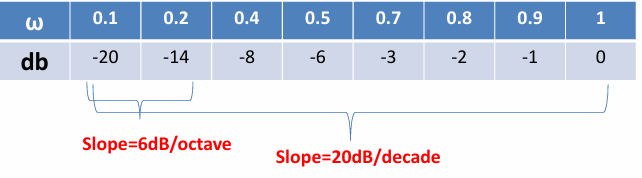
此时可以发现,频率每增加10倍,幅值上升或下降20dB,因此:
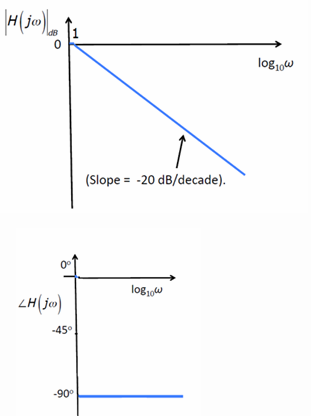
- 积分器$\frac{1}{s}$对幅值的影响是-20dB/decade
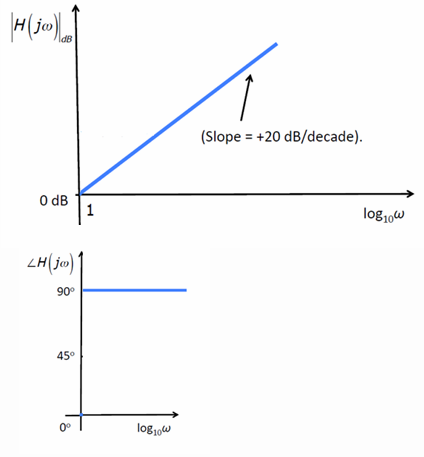
- 微分器s对幅值的影响是+20dB/decade
- 有几个微分器或者积分器,就叠加几次;例如有两个微分器,就是-20dB/decade+(-20dB/decade)=-40dB/decade
(2)积分或微分对相频图的影响
考虑一个只有微分器或者积分器的系统,也就是说它的实部为0,虚部由微分器或积分器引入:
- 微分器系统内$虚部=j\omega$,实部等于0,因此向量在正虚轴上,相位为$+90\degree$
- 微分器系统内$虚部=\frac{1}{j\omega}=j\frac{1}{-\omega}$,因此向量在负虚轴上,相位为$-90\degree$
如果系统内有多个积分器或微分器,他们会互相约掉,只留下最多的;例如假设有2个积分器4个微分器,$\frac{1}{s^2}{s^4}=s^2$,此时$虚部=j\omega^2$因此在正虚轴上,相位为$+90\degree$;
换句话说,如果微分占主导,则为$+90\degree$;如果微分占主导,则为$-90\degree$
下图分别展示了微分器(左)积分器(右)的影响。
 |
 |
增益
增益只作用于传输函数的分子,是一个常数项,用K表示。例如$\frac{K}{s+1}$。如果把这个K提出来,可以理解为将系统$\frac{1}{s+1}$的结果放大了K倍。将增益从传输函数内剥离:
同样地,$G’(s)$表示剥离了增益剩下的传输函数。
(1)对幅频图而言
(在下面默认增益为正)
所以,增益对幅频图而言,会将其整体抬升$20log(K)$
(2) 对相频图而言
增益的影响并不会改变虚部和实部的比例,因此它的相频图无影响
一阶系统
一个一阶系统的s域表示是$(Ts+1)^{\pm 1}$。我们还是将其从一个传输函数内剥离开,和前面一样的思想,这里就不重复了。
(1)对幅频图而言
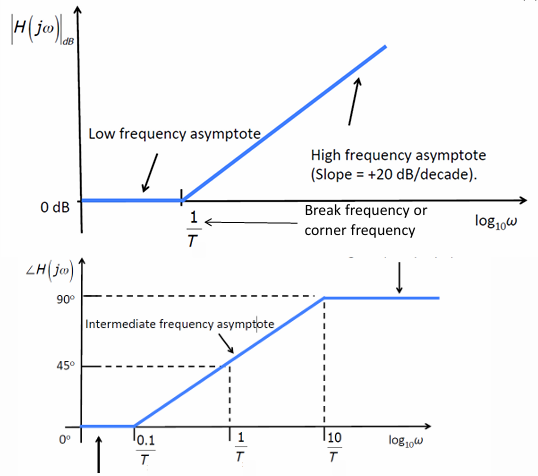
- 当$(\omega T)^2$很小时,可以近似忽略掉它,认为其对幅值的影响为0;这个很小的界限是$\omega<<1/T$,在这里为了方便就取$\omega<1/T$。我们将$\frac{1}{T}$称为Break frequency 或 corner frequency;
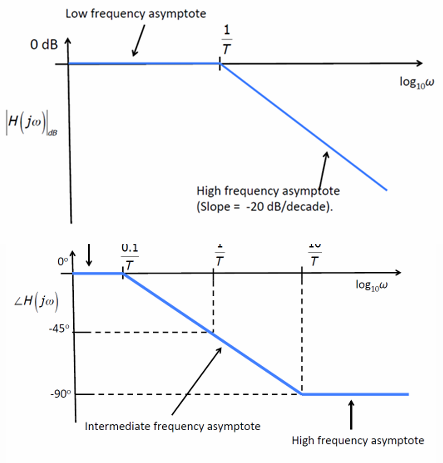
- 当$(\omega T)^2$很大时,可以近似忽略掉1,认为其对幅值的影响是$\pm 20log(\omega T)=\pm[20log(\omega)+20log(T)]$。这以引入里面那个波德图举例,因为T一般小于1,因此$20log(T)$一般为负值,代入$-[20log(\omega)+20log(T)]$相当于加了一点增量,这就是引入里面那个图在下降点附近有略微抬升的原因,即,高阶系统需要对谐振频率进行抬升补偿的原因。因为近似法只是求个大概,因此这里忽略这个20log(T)。因此当$\omega>1/T$时,认为其和积分器一样,提供20dB/decade 的上升或下降。
PPT下面会介绍二阶系统的谐振频率补偿,后面不会用,笔记省略了,但是这里展示了为什么会产生谐振峰值振幅。
(2)对相频图而言
- 对于$(Ts+1)^{1}$,在$s=j\omega$很小时,几乎由实部1占据主导,因此其相位是$0\degree$;而当$s$大到一定程度,虚部会慢慢发力,会慢慢将相位拉到90°。认为这个很小的界定点是$s=\frac{T}{10}$,认为很大的界定点是$s=10T$。这刚好是2个decade变化90度,因此斜率为$45\degree/decade$
- 同理,对于$(T_s+1)^{-1}$,在$s=j\omega$很小时,其相位是$0\degree$;而当$s$大到一定程度,会慢慢将相位拉到-90°。斜率为$-45\degree/decade$
分别如下面2图所示
 |
 |
PPT上有一种先分别画出微(积)分器、增益、一阶系统三者波德图,再将其叠加的方法(相当于分别考虑其三者对幅度和相位的影响,再叠加在一起),但是这种方法不好用,就不在这里详细介绍了,看懂了上面的推导应该可以轻易看懂PPT上的叠加法。
五星级归纳和五星级起始幅度相位确定
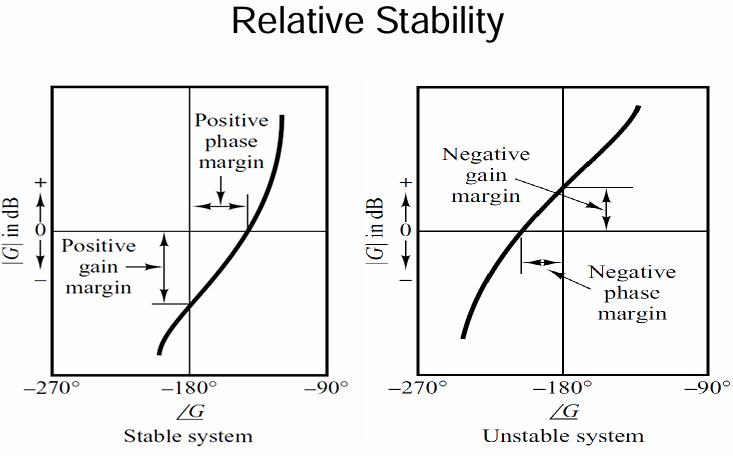
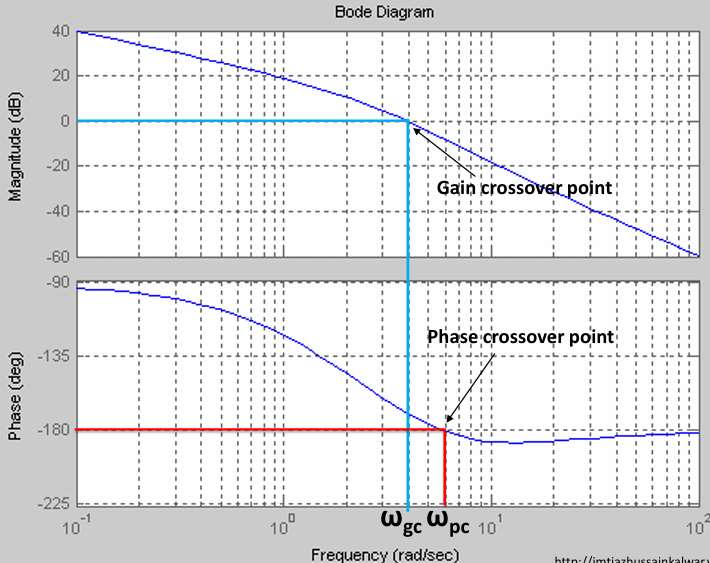 - **幅值裕度(gain margin,GM)**:0dB与 在 相位穿越频率对应的幅度值 的差值,即:$0dB-Magitude(\omega_{phase\ crossover\ frequency})$
- **相位裕度(phase margin,PM)**幅度穿越频率对应的相位 与 -180° 的差值,即:$Phase(\omega_{magitude\ crossover\ frequency})-(-180\degree)$=$Phase(\omega_{magitude\ crossover\ frequency})+180\degree$
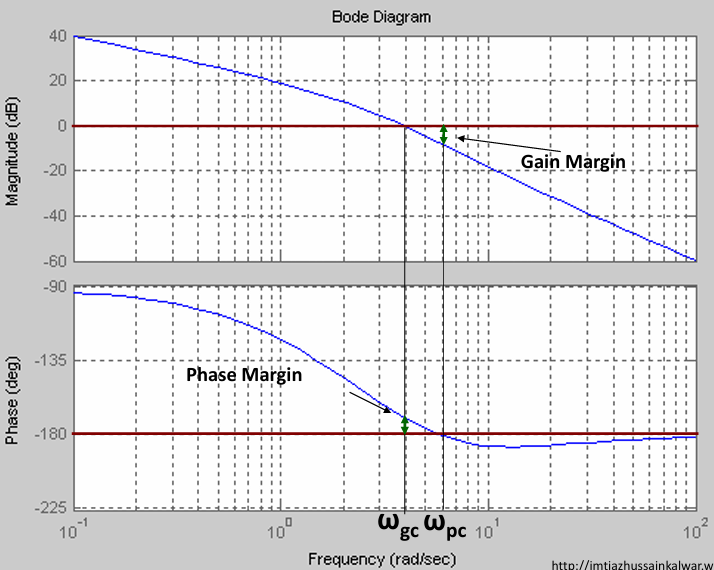
### 幅值裕度、相位裕度与稳定性的关系
- **幅值裕度(gain margin,GM)**:0dB与 在 相位穿越频率对应的幅度值 的差值,即:$0dB-Magitude(\omega_{phase\ crossover\ frequency})$
- **相位裕度(phase margin,PM)**幅度穿越频率对应的相位 与 -180° 的差值,即:$Phase(\omega_{magitude\ crossover\ frequency})-(-180\degree)$=$Phase(\omega_{magitude\ crossover\ frequency})+180\degree$

### 幅值裕度、相位裕度与稳定性的关系
五星级关系
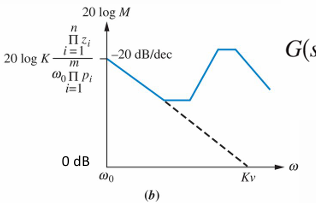
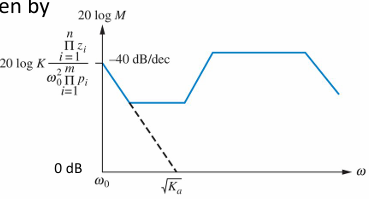
极坐标图 (Polar plot)
引入-什么是极坐标图
对于一个系统,它的开环系统函数为$GH(s)$,这是一个复数,可以写成$|GH(j\omega)|\angle(\theta)$或者$Real(GH(j\omega))+jImg(GH(j\omega))$的形式。
而回想一下坐标轴呢:
在极坐标系下,向量在坐标上的位置由其模长和角度决定,对应$|GH(j\omega)|\angle(\theta)$.
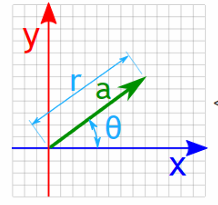
在笛卡尔子坐标系下我们把X轴定义为实轴,Y轴定义为虚轴,对应$Real(GH(j\omega))+jImg(GH(j\omega))$;
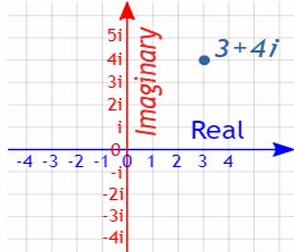
这两种坐标轴其实画出来的图像是完全一样的。
极坐标图就是在这样的坐标图下,把$s$从$0\rightarrow +\infty$时$GH(s)$的值画在坐标上。例如下面这个例子
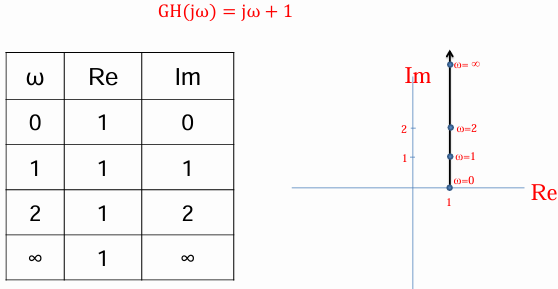
极坐标图的优势是:
- 极坐标图的优势在于可以在一个紧凑的图表中显示完整的频率响应信息
- 每种类型的传递函数都对应于一个特征轨迹,其基本性质很容易记住
如何绘制极坐标图
- 求出开环传输函数OLTF,将$s=j\omega$代入
- 求出$\omega=0$时$GH(j\omega)$的值,这是极坐标图的起始点
- 求出$\omega=\infty$时$GH(j\omega)$的值,这是极坐标图的终点
- 通过$Img(GH(j\omega))=0$解出$\omega$来检查其是否和实轴相交,并解出交点
- 通过$Real(GH(j\omega))=0$解出$\omega$来检查其是否和虚轴相交,并解出交点
- 再找几个$\omega$介于这些特殊点间的值,来提高绘图精度
- 平滑的曲线连接这些点
举个例子:$G(s)=\frac{1}{s(s+1)}$
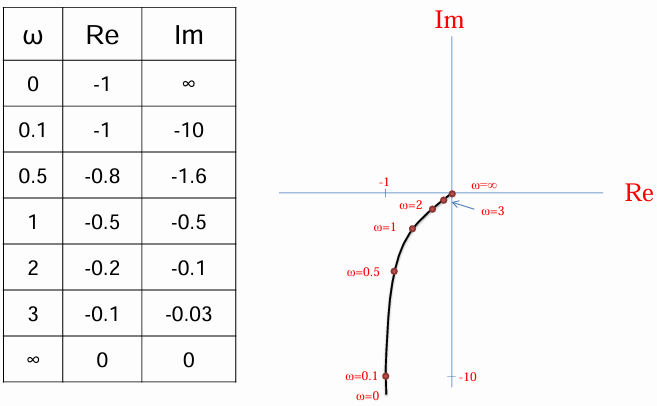
奈奎斯特稳定性准则(Nyquist Stability Criterion)
前置知识-柯西幅角定理 (Cauchy’s Argument Principle)
(参考资料中对柯西幅角定理进行了证明,若有兴趣可以自行了解)
柯西幅角定理:复平面1上的点通函数$F(s)$映射到复平面2(也就是,复平面1是s的值,复平面2是$F(s)$的值)。现有封闭曲线$C_S$包围复平面1上函数$F(s)$的Z个 零点和P个极点。当封闭曲线$C_S$以顺时针方向包围一周时, 在复平面2上也会有封闭曲线$C_F$将以逆时针方向绕原点旋转 N=P-Z 圈
- 若N为正数,则$C_F$以逆时针方向环绕,且包围原点;
- 若N为0,则$C_F$以顺时针还是逆时针方向环绕不确定,但不包围原点;
- 若N为负数,则$C_F$以顺时针方向环绕,且包围原点;
也就是说,可以通过经过函数映射的复平面的旋转关系,来判断画出来的线内是否包含零极点。如果我们去画一条包围s域右半平面的线,再去看经过系统函数映射出来的线的图像,那么是否就可以判断s平面右半包不包含零极点了?
奈奎斯特路径(Nyquist path)
上文提到的“一条包围s域右半平面的线”,就被称为奈奎斯特路径,也叫Nyquist counter。
奈奎斯特路径是 s 平面中的闭合等值线,它完全包围了 s 平面 的整个右半部分(Right Half Plane, RHP),同时不穿过(绕行)虚轴上或位于 0 处的 $G(s)H(s)$ 的任何极点。
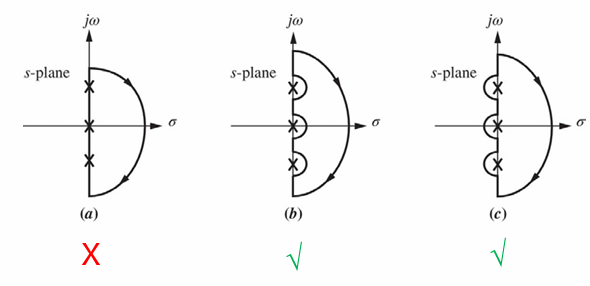
绘制奈奎斯特图
奈奎斯特图是极坐标图的延续,极坐标图的扫频范围是$0$到$\infty$,而奈奎斯特图的扫频范围奈奎斯特路径定义的范围。画图步骤如下:
如果$G(s)H(s)$在虚轴上没有极点,则:
- 解算出$G(s)H(s)$在虚轴的所有零极点
- 绘制从$\omega=0$扫频到$\omega=\infty$的极坐标图;此时完成了奈奎斯特路径上线条ad的扫频
- 绘制从$\omega=-\infty$扫频到$\omega=0$的极坐标图;此时完成了奈奎斯特路径上线条fa的扫频
- 求得$s=\lim_{R\rightarrow\infty}{Re^{j\theta}},-90\degree<\theta<90\degree$时$G(s)H(s)$的解,对应线条def,通常这个解会趋于一个点。
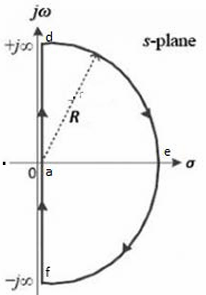
如果$G(s)H(s)$在虚轴上有极点,则:
在前面四步的基础上,需要执行第五步:
- 取$s\rightarrow poles$但不等于,半径为$\lim_{\rho\rightarrow0}{\rho e^{j\theta}}$,对极点进行绕行
举个例子
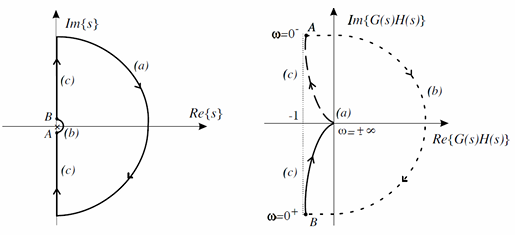
对于系统开环传输函数:
- 首先取$\omega=0^+$扫频到$\omega=\infty$的,可以画出路径下半平面的(c)
- 首先$\omega=0^-$扫频到$\omega=-\infty$的,可以画出上班平面的路径(c)
- 取$s=\lim_{R\rightarrow\infty}{Re^{j\theta}},-90\degree<\theta<90\degree$,对应的是$G(s)=0$这个点
- 取$s\rightarrow 0$且距0半径为$\lim_{\rho\rightarrow0}{\rho e^{j\theta}}$,$90°<\theta<-90°$对其进行绕行,对应是$|G(s)|\rightarrow \infty,$90°<\theta<-90°$,即路径(b)
奈奎斯特稳定性判
要研究系统是否稳定,就是去研究它的闭环传递函数的所有极点都在左半平面。然而,闭环传递函数是
我们现在的讨论都是基于开环传递函数$G(s)H(s)$做的,如何将它们关联呢?
令$G(s)=\frac{N_G}{D_G}$,$H(s)\frac{N_H}{D_H}$
此时我们发现,$G(s)H(s)$和$1+G(s)H(s)$的分母相等,即二者极点相等。$1+G(s)H(s)$的分子和$\frac{G(s)}{1+G(s)H(s)}$的分母相等,即$1+G(s)H(s)$的零点和$\frac{G(s)}{1+G(s)H(s)}$的极点相等。
此时,可以发现,$1+G(s)H(s)$的极点和$G(s)H(s)$的极点相同;
假设现在这个用作映射的函数$F(s)=1+G(s)H(s)$,那么$N=P-Z$的意义就是,被s域右半平面框住的$G(s)H(s)$的极点个数减去$\frac{G(s)}{1+G(s)H(s)}$的极点个数;
我们将$F(s)$左右同时减1做为新的映射函数,$F’(s)=F(s)-1=G(s)H(s)$。因为这个映射是线性的,所以对于映射过去的绕圈圈的图就是把围绕(0,0)绕圈变成了围绕(-1,0)绕圈,其他性质不变(即零极点让它绕圈的方向和次数)。这个$F’(s)$,就是奈奎斯特图的映射了。
我们知道,当$\frac{G(s)}{1+G(s)H(s)}$右半平面出现极点时,即$Z!=0$时,系统就不稳定。若$Z=0$,那么系统就稳定。换句话说,也就是N=P时,系统稳定。N代表的是绕圈的圈数,P代表的时OLTF的极点个数。至此我们得到了奈奎斯特稳定性判据。
奈奎斯特稳定性判据:当奈奎斯特图绕圈的圈数等于OLTF右侧极点个数时,系统稳定。(N=P 或 N=P-Z, Z=0)
举个例子
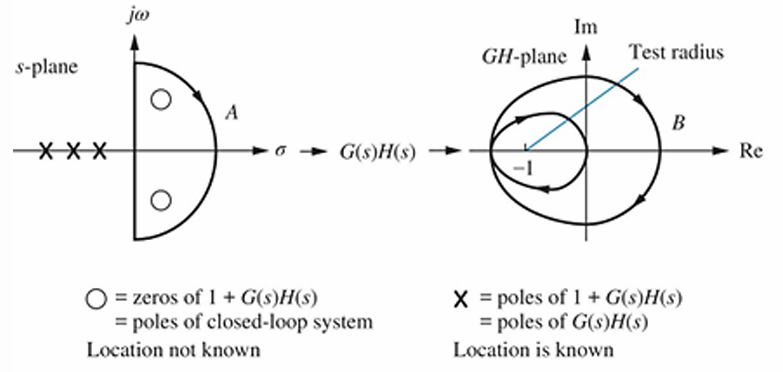
对于上图,被奈奎斯特路径框住的零点有2个,因此Z=2;极点0个,因此P=0;$N=P-Z=-2$,因此奈奎斯特图顺时针绕两圈。但是由于$N!=P$,所以系统不稳定。
奈奎斯特图与幅值裕度和相位裕度的关系
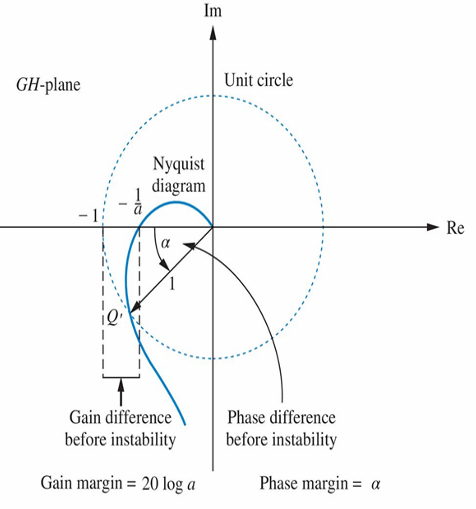
回顾前面,幅值裕度是指的$0dB-相位穿越频率下的幅度$的值。而奈奎斯特图下,某一点距原点的距离就是其幅值,距离正半轴的角度是其相位。
相位穿越频率是相位等于$-180°$的时候,也就是其与负半实轴的交点。而0dB就是增益为1时,也就是单位圆。也就是说,幅值裕度就是$20log(1-负半实轴交点的幅值)$。
同理可得,相位裕度就是$曲线与单位圆的交点的相位-180°$。如下图所示
尼柯尔斯图 (Nichols Chart)(了解即可)
引入-M环和N环
M环
常数 M 环(Constant M-Circles)是单位反馈系统的闭环幅度频率响应的轨迹。
假设有一个单位反馈控制系统:
代入$s=j\omega$,去掉拉普拉斯变换的衰减常数;并将其虚部和实部拆分。
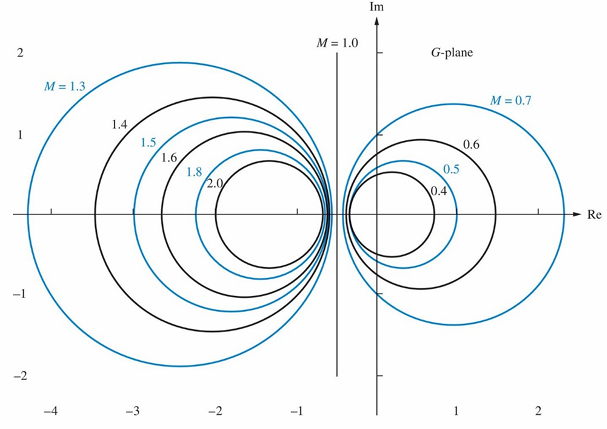
那么这个信号在某一频率$\omega$下的幅度就是$|T(j\omega)|$,记幅度为$M$,有:
这个式子经过移相改写之后可以改写成一个圆的表达式(这里就不推了,这不是重点),圆的大小随着M的大小变化而变化,如下图所示
N环
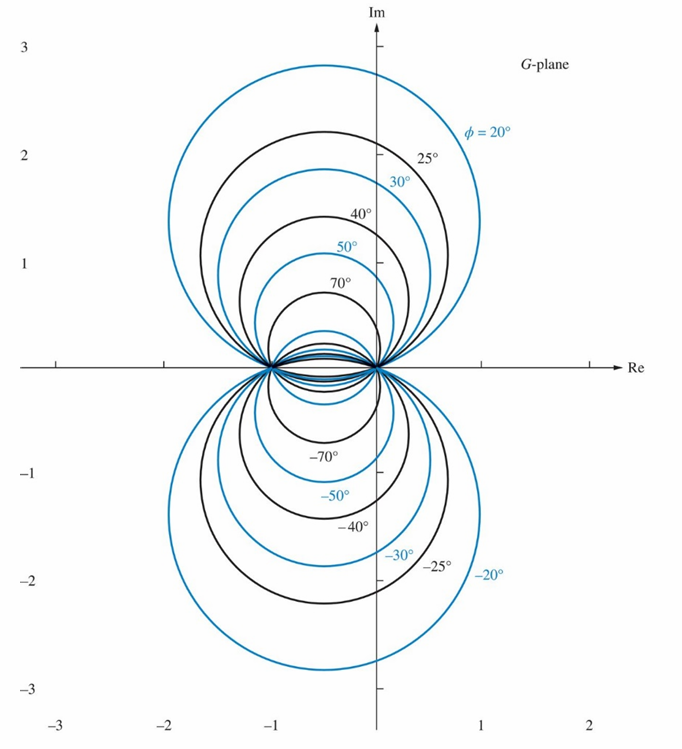
常数 N 环(Constant N-Circles)是单位反馈系统的闭环相位频率响应轨迹。
对于和M环一样的系统:
这个也是个随着相位$\phi$改变而增大的圆
使用极坐标表示的幅度和相位,那不就是N环和M环的交点吗?
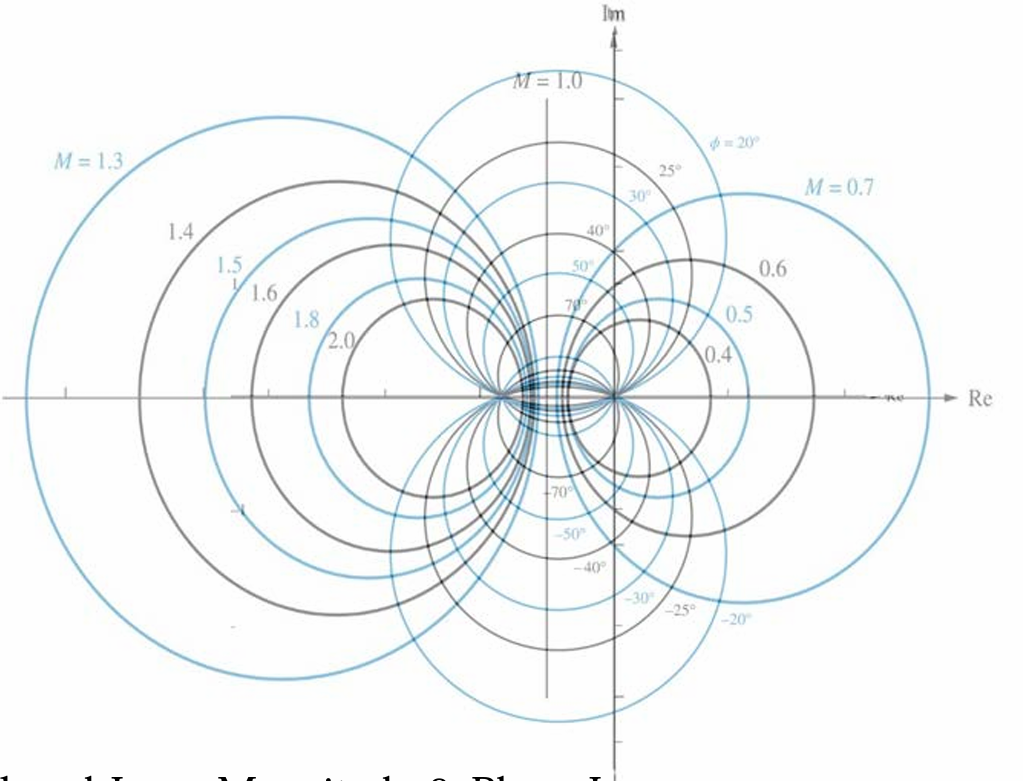
尼柯尔斯图
在上面的M环和N环中,是M环和N环都没有以对数形式给出。而尼科尔斯图对其进行了改进,尼柯尔斯图是将线性非时变系统在不同频率下的增益分贝值及相位绘在一直角坐标系的图上,尼柯尔斯图将二种波德图(波德增益图及波德相位图)结合成一张图,而频率只是曲线中的参数,不直接在图中显示。
尼科尔斯图的坐标有两部分:
- 下面和右侧的线性坐标表示OLTF的幅值和相位,其中横轴表示开环相位,纵轴表示开环幅值
- 中间一圈一圈的表示M环和N环
画尼科尔斯图时,只需使用开环传递函数,和画极坐标图类似的操作即可。
例如:
这是开环传递函数,从$0-\infty$范围内进行扫频,求得OLTF的幅值和角度,对应线性坐标系标上去即可。
这条线和非线性坐标系交点处由M环和N环得出的闭环传输函数特征。
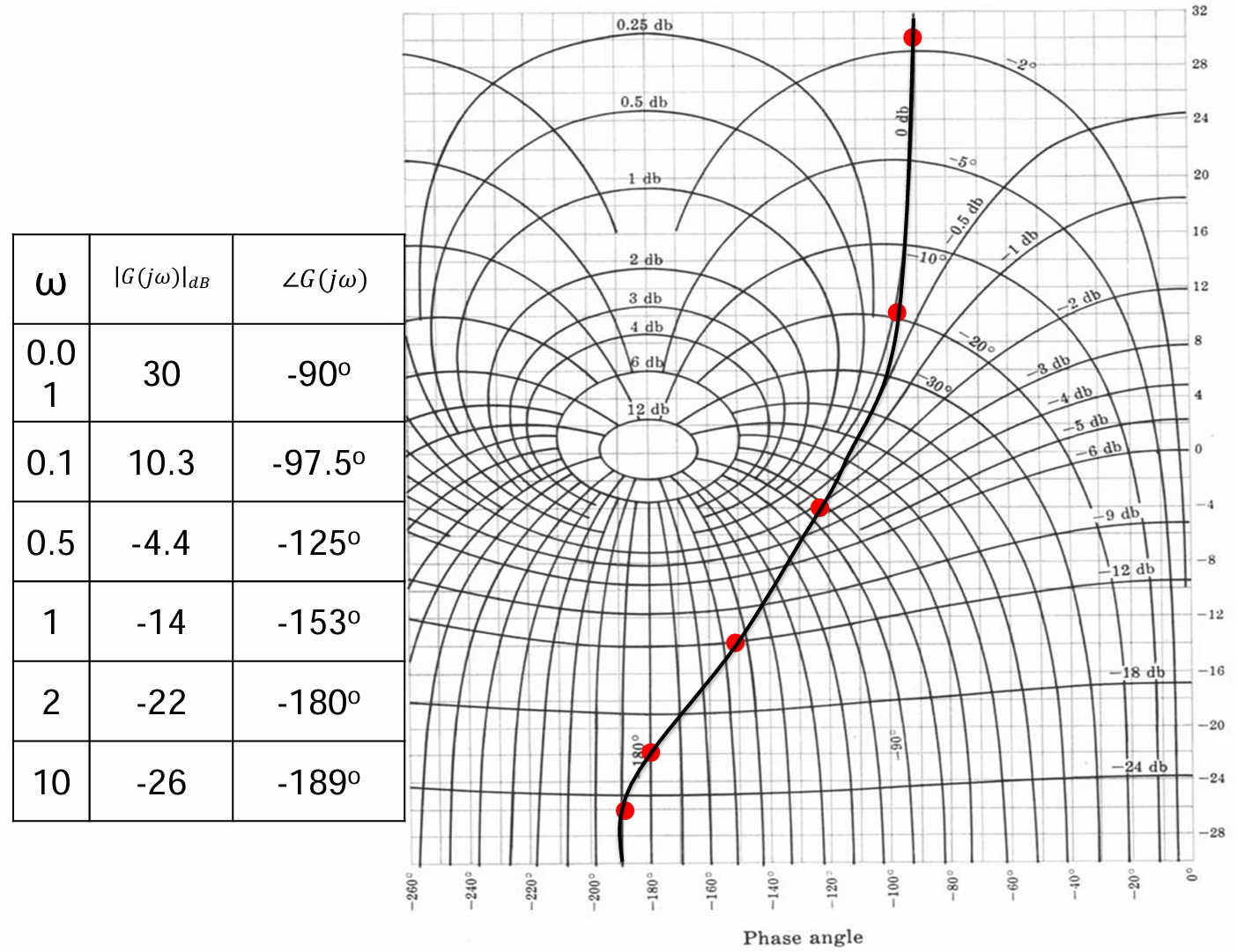
其幅值裕度和相位裕度如下图,都是线性坐标系下的交点。