预补偿器（Pre-Compensator）的介绍

预补偿器和上文PID控制器位于系统中同一位置，它旨在用于调整系统响应的各个方面，包括稳态误差、Overshoot、setting time等等。在不重新设计整个控制系统的情况下，使用预补偿器是一种相对简单的方法来修改系统。PID其实就是一种特殊的预补偿器。

它的优点有：

简单：无需重新设计整个系统
精确：可以通过对与补偿器的设计来消除系统稳态误差
灵活：它可以影响系统的方方面面而不直接修改系统

它的缺点有：

带宽限制：提高稳态误差性能会导致带宽变窄，从而影响系统快速响应变化的能力。
稳定性问题：如果设计不当，添加预补偿器可能会破坏系统的稳定性，特别是如果引预补偿器入了明显的相位滞后。
设计中的复杂性：对于某些系统，设计有效的预补偿器需要对系统响应进行复杂的分析和理解，这可能既复杂又耗时。

根轨迹下预补偿器的设计

前置知识：如何判断根是否在根轨迹上

频率响应下的预补偿器（Pre-Compensator）设计

引入-PID控制器与与补偿器的关系

PI控制器

前面提到PI控制器有消除稳态误差的能力。PI控制器的通式为：

$G_c(s)=K_p(1+\frac{1}{K_is})=\frac{K_pK_is+1}{K_is}$

但是由于PI控制器给分母引入了孤立s，会改变系统的类型造成高频衰减，从而破坏原本调好的动态响应。有没有什么类 PI 补偿的表达式，它在 s = 0 时产生显著的增益，从而减小稳态误差，但在较高频率下几乎为 1，对动态响应没有影响呢？

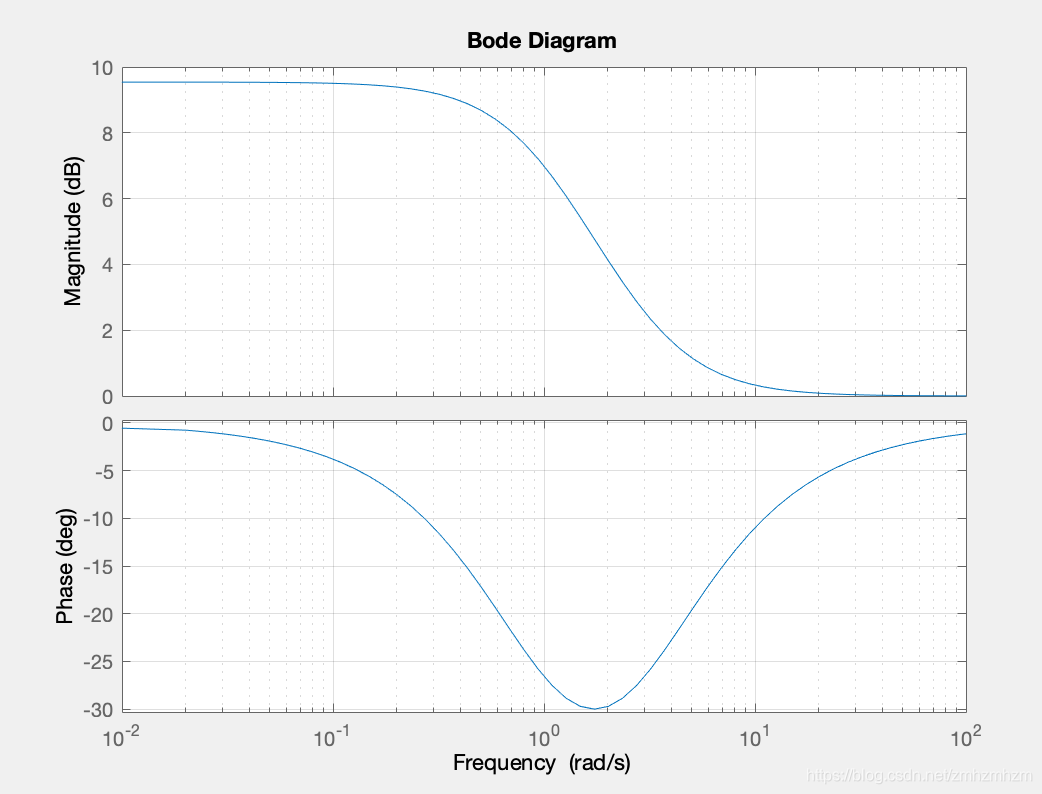
答案就是在分母上将在原点的极点移动一下，移动成靠近0的极点，这个极点的影响范围主要在低频（回顾波德图，0.1T-10T范围）。因此在低频时其幅频图还是收原来的PI控制器影响为主，但是在高频这个极点的贡献就失效了，而不像在直接在原点一样对全频有效；同时也因为这个移动，导致稳态误差无法彻底被消除，因此设计时还是需要考虑稳态误差。这就是相位滞后补偿器（Phase Lag Compensator）。

$G_{lag}(s)=K\frac{\tau s+1}{\alpha\tau s+1},\alpha>1$

在这个表达式下，又保留了s = 0 时产生显著的增益，从而减小稳态误差的特性。管他叫滞后补偿器的原因是这个补偿器函数的波德图相位是负数，如下图。

在这里插入图片描述

PD控制器

前面提到PI控制器有增加相位裕量的能力（增加系统稳定性）；同时，不影响稳态误差。其通式为：

$C(s)=K_p(1+K_ds)$

我们注意到，PD 补偿的幅度会随着频率的增加而不断增大。这一特性并不受欢迎，因为它会放大高频噪声。

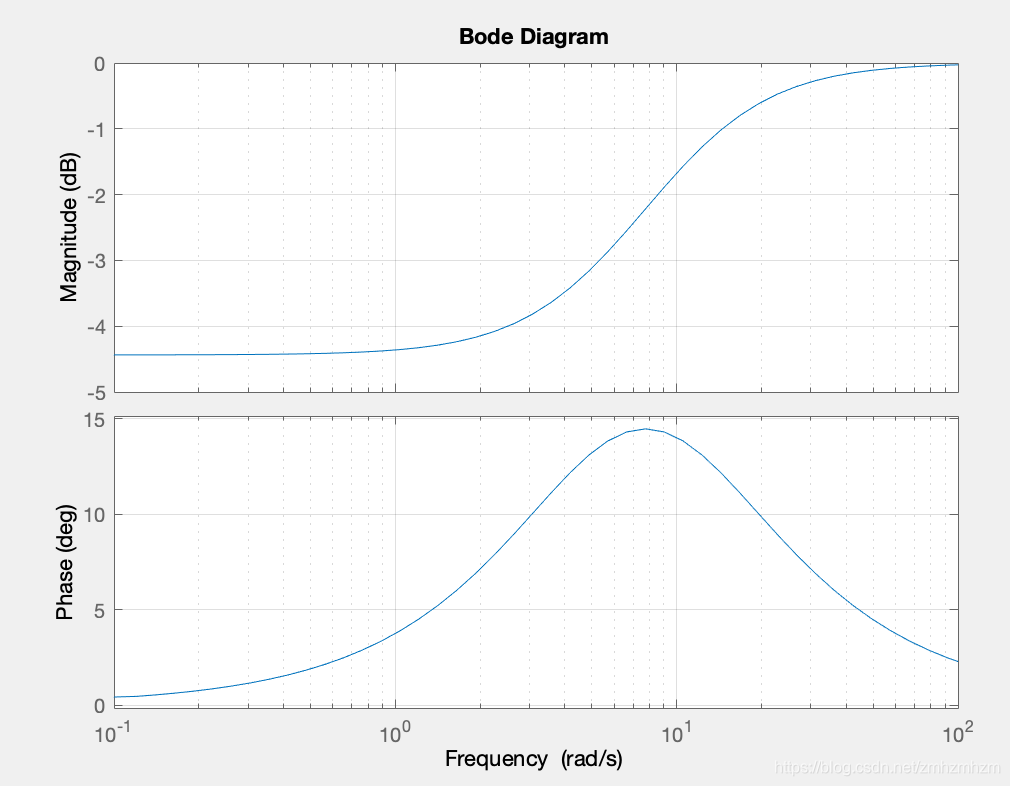
为了减轻 PD 补偿的高频放大，在比 PD 补偿器高得多的频率处，在分母中添加了一个一阶极点来抵消零点的增益（可以回顾波德图，这个一阶极点的影响范围会被局限在高频）。这就是超前补偿器（Phase Lead Compensator）。

$G_{lead}(s)=K\frac{\tau s+1}{\beta\tau s+1},\beta<1$

管它叫超前补偿器的原因是补偿器函数波德图的相位是正数，如下图：

在这里插入图片描述

超前-滞后补偿器介绍

滞后补偿器

用途：主要用于改善稳态误差，而不会显著影响系统的稳定性裕度。

工作原理：滞后补偿器通常在系统的传递函数中添加一个极点和一个零点，零点位于极点的左侧。这种配置增加了低频增益，而不会显著影响高频增益（高频零极点同时发力了），从而通过增加系统的类型或其直流增益来提高系统跟踪稳态值（如阶跃响应）的能力。

应用：适用于需要稳态精度但不希望对瞬态响应或高频特性进行重大修改的系统。

超前补偿器

用途：旨在改善系统的瞬态响应，包括减少上升时间、建立时间和增加相位裕量（从而提高稳定性）。

工作原理：超前补偿器在系统的传递函数中引入零点和极点，零点位于极点左侧）。在低频时以零点提供的为主导，使系统响应更快、响应速度更快。

应用：通常用于使系统响应更快或使边缘稳定系统稳定的情况。它们在控制系统中很常见，因为控制系统的响应速度和稳定性比稳态精度更重要。

超前-滞后补偿器

用途：结合超前和滞后补偿器的特性，以改善系统的瞬态和稳态响应

工作原理：超前滞后补偿器引入了两组极点和零点：一对提供相位超前（改善瞬态响应），另一对提供相位滞后（改善稳态误差）。该设计更加复杂，它旨在平衡瞬态和稳态性能之间的权衡。

应用：需要稳态精度和良好的瞬态响应。它们用于需要稳定响应、减少过冲和确保稳态误差符合设计规范的系统。示例包括航空航天、机器人和汽车工程中的先进控制系统。

从补偿效果的角度来理解超前和滞后补偿器

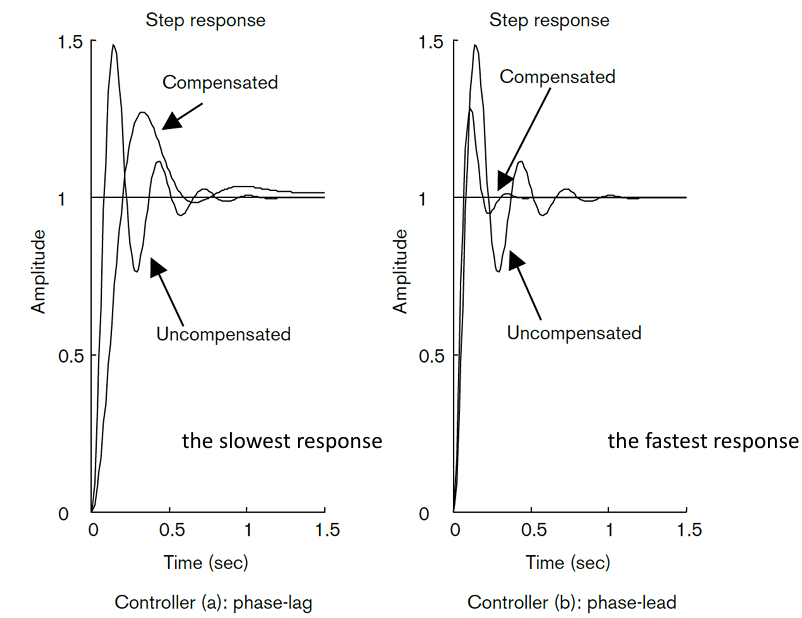
下图展示了分别有超前补偿器和滞后补偿器补偿的单位阶跃响应。

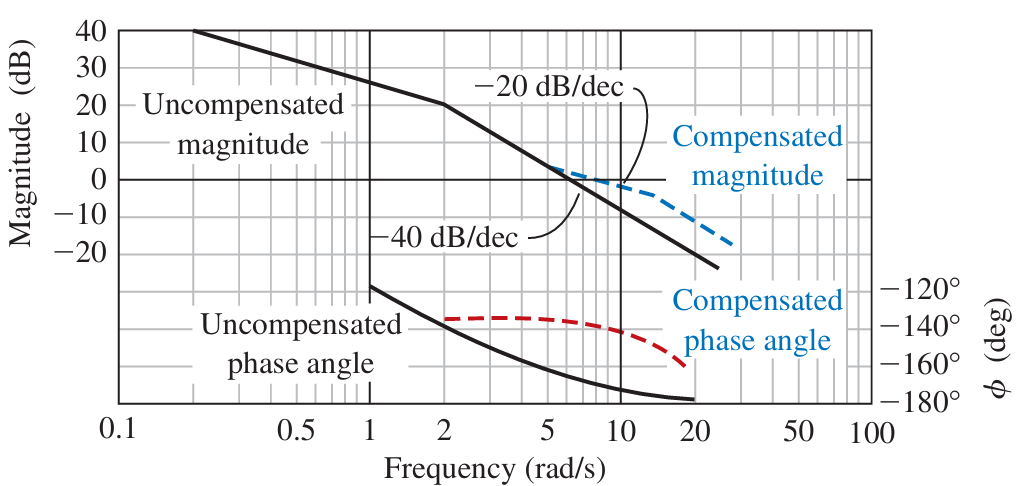
下图是超前补偿器对系统补偿前后的波德图。可以看到超前补偿器对高频信号有一个增益，同时补偿后的相位也领先于补偿前的；

下图是滞后补偿器对系统补偿前后的波德图。可以看到滞后补偿器对高频有明显衰减（相对而言就是对低频的增益），同时补偿后的相位滞后于补偿前的。

请注意，超前补偿器或滞后补偿器不是超前补偿器增加相位裕度、滞后补偿器减少相位裕度。超前补偿器虽然整体抬高了相位裕度，但是它也抬高了高频，导致幅值穿越频率靠后。滞后补偿器虽然整体减小了相位裕度，但是也削减了高频，导致幅值穿越频率靠前。通常来说，这两种补偿器最终的结果都是保持或增加了相位裕度。

超前、滞后补偿器设计

系统参数要求

设计要求通常以稳态误差和相位裕度的约束形式给出，例如：

对于某种输入，要求$e_{ss}<0.01$
要求$PM>45^\circ$

如果设计要求是阻尼比，那么对于具有二阶特性的系统，我们可以使用以下关系将其转换为近似的相位裕度要求：

$PM(degrees)\approx100\zeta$

滞后补偿器设计

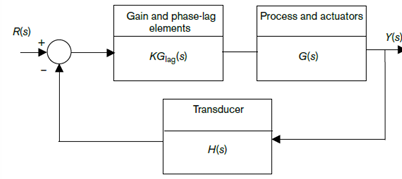
记单位增益的相位滞后系统传输函数为$G_{lag}(s)$，前面提到，它无法完全消除稳态误差了。而稳态误差$e_{ss}=\frac{1}{1+\lim_{s\rightarrow0}{KG_{lag}(s)}}$可以通过加增益K来尽可能减小。因此，设计的第一步就是找到一个K来满足$e_{ss}$。
有了K之后，可以画出这个系统相位滞后补偿时开环传递函数的波德图，即$KG(s)H(s)$的波德图，找到系统目前的幅度穿越频率和其对应的相位裕度（记为$PM_{sys}$）
根据系统要求的参数，可以计算出一个新的相位裕度要求，记为$PM_{spec}$。此时我们的目标是通过滞后补偿器将系统新的相位裕度削减成$PM_{spec}$。由于$PM_{spec}$是使用经验公式约等于出的，同时下面介绍的计算补偿量的方法也不完全精确，因此通常需要额外补偿一下。将这个额外补偿的量记为$\phi_c$。
在前面画的波德图上，找到$PM_{spec}+\phi_c$对应的穿越频率$\omega_{gco}$。要使得当前系统的穿越频率变成这个新的$\omega_{gco}$，就需要给一个负增益，记为$K_{red}$。直接当前波德图将$\omega_{gco}$这一点的$幅值-0dB$即可拿到$K_{red}(dB)$
我们根据下面的公式来计算系统参数：

$\tau=10/\omega_{gco}$ $\alpha=10^{K_{red}/20}$ $G_{lag}(s)=\frac{\tau s+1}{\alpha \tau s+1}$

至此我们求到了补偿器；再画出补偿器的波德图，看一看$PM$是否削减到位，如果不到位就再补狠一点再试。

总体来说，设计步骤可以归纳为下图：

举个例子

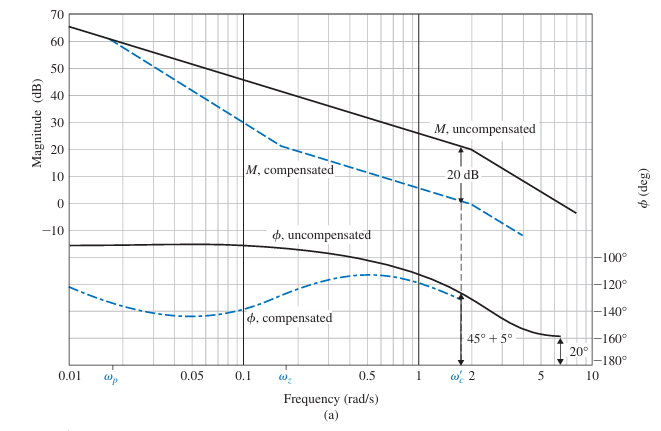
要求给如下系统设计一个补偿器，使得$K_V<5 sec^{-1}$ ,相位裕度至少$40^\circ$，幅值裕度至少$10dB$，$\phi_c=12^\circ$

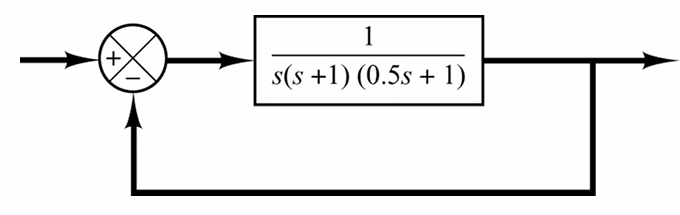
首先根据CH1中介绍的寻找Unit ramp 输入下稳态速度常数的公式计算出需要的增益：

$K_v=\lim_{s\rightarrow0}{sKG(s)}=K=5$

因此$K=5$

画出$KG(s)$的波德图，如下图所示

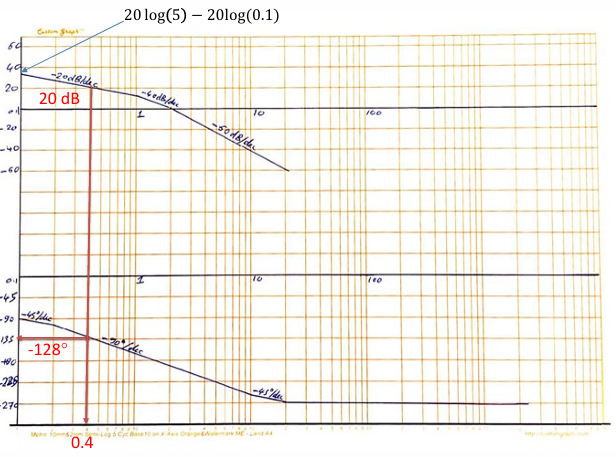
需要的相位裕度是$$

由于滞后相位补偿器在低频点会有一个增益，这会导致幅频曲线抬高$\omega_{gco}$后移而，而下面根据补偿量计算补偿器参数的公式并没有考虑这个后移，因此可以适当多补偿一些，多补偿的值记为$\phi_c$，称为additional phase angle，使得系统。

找到一个新的$\omega_{gco}$，使其满足期望的相位；

超前补偿器设计

类似于滞后补偿器，超前补偿器的设计总结为下表。