Control-Systems-Part2-Lectrue1~3-数字控制系统基础

数字控制系统简介

数字控制系统的核心是使用MCU、电脑之类的控制器通过软件的形式对数据进行处理。而不是模拟信号那样通过模拟器件来构成积分器微分器等等。

数字控制系统具有如下优点：

• 对噪声的鲁棒性好：数字信号可以无损传输，只要不超过门限值，数字信号读取出来都是无损的。
• 灵活性高：数字控制系统主要通过软件编程来实现对数据的处理，这样的系统灵活性高，重新刷写程序即可设计新的系统
• 成本：数字系统的可靠性在升高而成本在下降
• 易用性：大规模集成电路可以更轻易地集成数字IC，这对数字信号处理更加友好

数字控制系统的基础-ADC和DAC

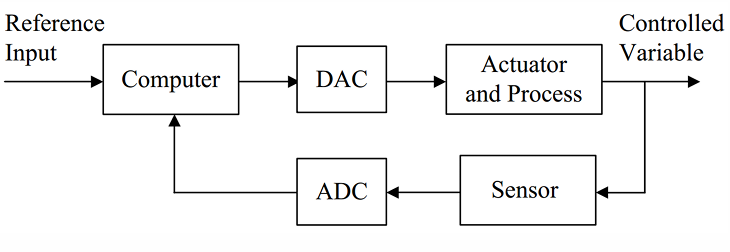
一个基本的数字系统如上图所示，其模拟输出的数字信号必须经过DAC转化为模拟信号交给模拟系统去执行，而反馈回来的模拟信号又必须通过ADC转化为数字信号以作为参考计算值。

DAC

有两种常用的DAC电路：

• R-2R 梯子（R-2R ladder）网络。
• 加权电阻器

R-2R ladder

下图是一个3bits R-2R DAC的电路图。$b_1$是LSB，$b_2$是MSB。让我们分析一下这个电路。

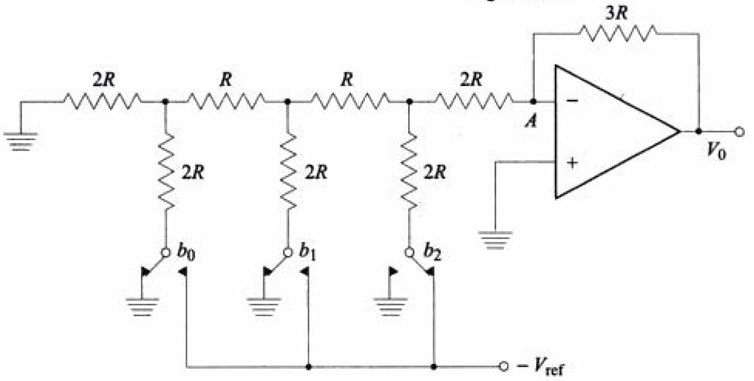
（1）上图这样$b_2$接通的状态，

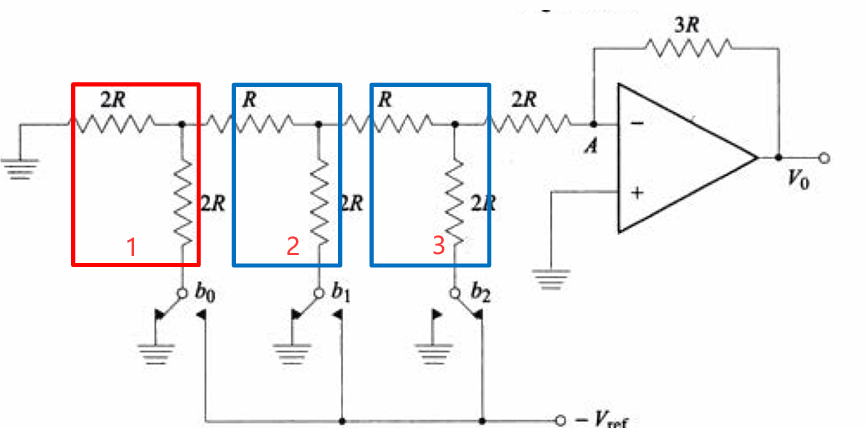
1. 将电阻器件编为3组。如上图1，2，3三个环。
2. 从最左侧第一组（环1）看起，水平的$2R$左侧接地，垂直的$2R$下面接地，因此以连接这两个$2R$的节点的视角来看，相当于两个等值对地并联电阻，因此在对节点来说它的等效电阻是$R$
3. 现在看到中间这个环2，它的水平方向有个$R$连接到（2）中的节点，然后再经过（2）中等效的$R$地，因此其水平方向对地阻值是$2R$。其竖直方向又是$2R$接地，因此站在它的节点的视角来看，它也是2个$2R$并联接地，可以等效为$R$。
4. 此时来到最后一组，水平方向的$R$和（3）中等效出来的$R$串联，阻值是$2R$。至此，电路等效成了这样：

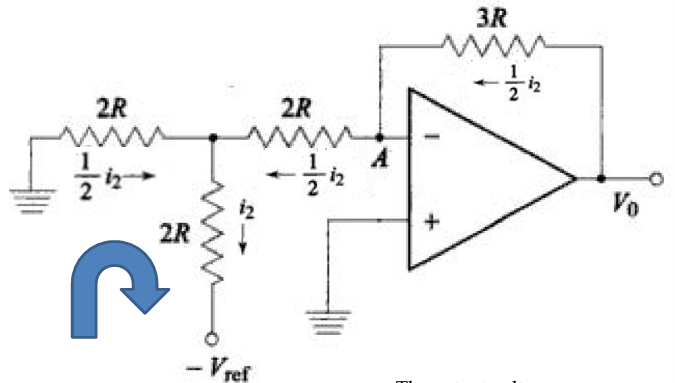
1. 上图中A点因为虚短电压为0V，因此水平方向的左右两个$2R$又可以等效为$R$。
2. 那么总电流就是$i_2=\frac{V_{ref}}{3R}$。同时水平方向的两个电阻均匀分流，因此流经运算放大器的电流是$\frac{1}{2}i_2=\frac{V_{ref}}{6R}$
3. 运算放大器的放大电阻为$3R$，因此输出电压$V_0=3R\times\frac{V_{ref}}{6R}=\frac{1}{2}V_{ref}$

回顾一下将DAC的映射规则：MSB贡献最大值的一半，剩下的bit是距离MSB有n位就贡献$(\frac{1}{2})^{n+1}V_{ref}$。例如$010$就是$1/4\times V_{ref}$。$111$就是$\frac{1}{8}V_{ref}+\frac{1}{4}V_{ref}+\frac{1}{2}V_{ref}$

现在是MSB为$V_{ref}$，其他bit接地的情况。即$100_{B}$的情况，$V_0$应当等于$\frac{1}{2}V_{ref}$，分析出来的电压和DAC的映射规则符合。

（2）让我们来试想一下LSB（$b_0$）接通，其他接地的状态。

1. 从环3开始看起，环3节点右侧水平的$2R$和竖直的$2R$都位于接地的状态，因此等效为$R$
2. 环$2$右侧水平的$R$和环3等效的$R$串联构成$2R$，并与竖直接地的$2R$等效成$R$
3. 至此从环1节点的视角来看，左侧为$2R$接地，右侧为$2R$接地，竖直为$2R$接$-V_{ref}$，这个情况和MSB为1时的第五步一模一样。因此流过环3竖直$2R$的电流也为$i_2=\frac{V_{ref}}{3R}$，水平方向左右两侧分别分流$\frac{V_{ref}}{6R}$。
4. 此时右侧的电流是流过运算放大器的，但是并非全部电流都经过运放的$3R$。当它经过环2时，站在环2的节点视角来看，水平为$2R$接地，竖直为$2R$接地，因此经过环2会被再次分走一半，只剩$\frac{V_{ref}}{12R}$。经过环1同理。如下图所示

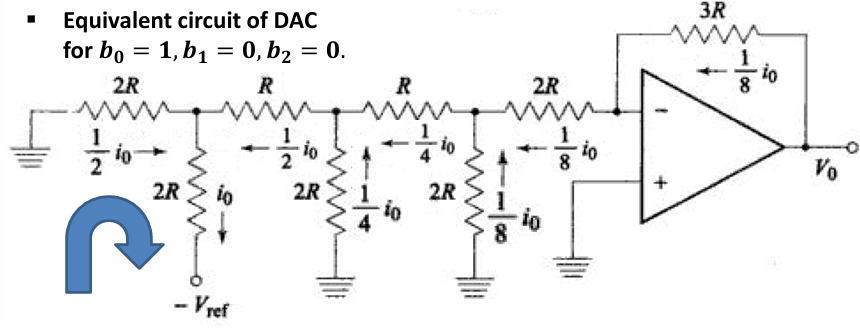
1. 最终流向放大电阻$3R$的电流为$\frac{V_{ref}}{24R}$，因此$v_0=3R \frac{V_{ref}}{24R}=\frac{1}{8}V_{ref}$
2. 总结一下我们发现，每经过1一个环，它的电流就变成了MSB电流的$1/2$，而距离MSB有n位就需要经过n个环，这恰好与DAC规则里面的“MSB贡献最大值的一半，剩下的bit是距离MSB有n位就贡献$(\frac{1}{2})^{n+1}V_{ref}$”对应上了。这就是这类DAC工作的原理

利用电流可叠加的特性，对每个bit接1的情况单独分析，即可发现$V_0$的输出是每个bit接地贡献电流的总和。至此这个DAC推导完毕。总结其通式为：

$$V_0=\frac{1}{2}(b_{n-1}+\frac{1}{2}b_{n-2}+...+\frac{1}{2^{n-1}}b_0)V_{ref}$$

weighted resistors

下图是weighted resistor DAC的电路图。

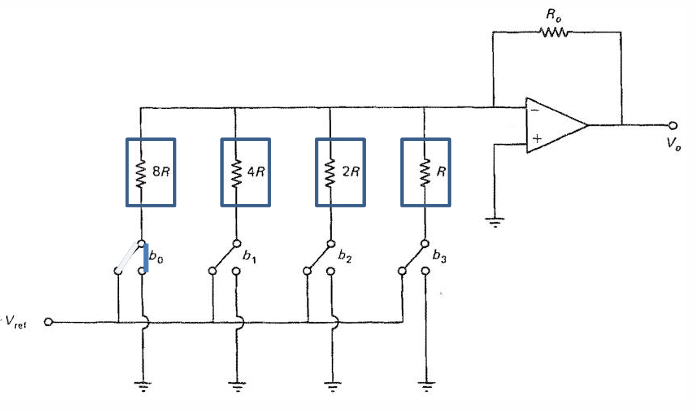
这类DAC的本质就是电子系统里面学过的反相加法器，通过不同的放大配置电阻来实现每个bit占不同的权重。这里省略推导。通式同上。

ADC-逐次逼近型ADC

这类ADC其实在计算机组成与接口一课中学过。这里简单回顾一下：

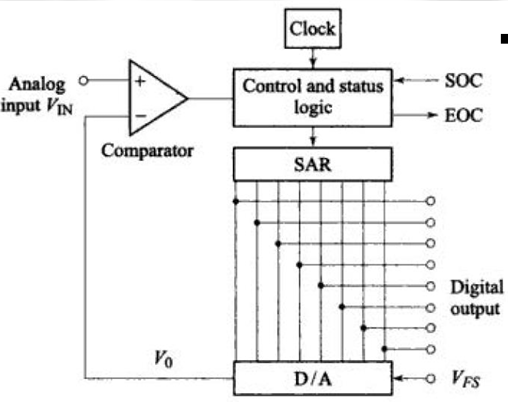
这类ADC由一个比较器，一个DAC，一个逼近寄存器（successive approximation register, SAR）,一个时钟信号，一个产生控制信号的控制器（SOC：Start of Converting; EOC: End of Converting）构成。

1. 一开始，SAR输出的值为0，DAC将其转换为模拟信号的0输出到$V_0$
2. 比较器比较$V_{IN}$大还是$V_{0}$大，如果$V_{IN}$大，则将MSB置位1；再次比较
3. 如果这次是$V_{0}$大，则将MSB回溯为0，MSB的后一位置为1；比较下一位
4. 如果还是$V_{IN}$大，则将MSB的后一位置为1；比较下一位
5. 重复这个过程，直到完成对最后一位的填写。

整个过程其实是一个二分法，如下图所示

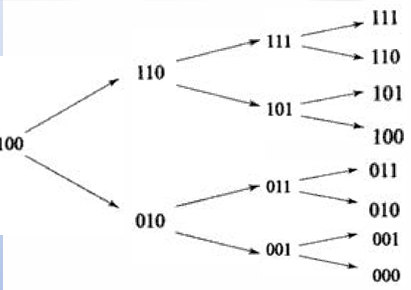
这种ADC的采样时间通常在$10ns-200us$不等，并且要求$V_{IN}$在采样期间保持稳定。高性能的ADC系统包括一个S/H（采样保持）器件，该器件在转换期间保持ADC的输入恒定。

数字采样的混叠（Aliasing）问题

当ADC以一个较低的频率去对模拟信号采样时，可能会出现下图这样的问题，导致采得的频率远小于信号实际的频率，这被称为Aliasing。

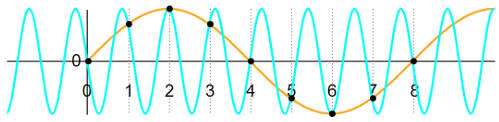
由于一个信号内会有不同的频率分量，因此有可能会有超出系统设计的高频频率分量因为Aliasing问题，在ADC采样后变成低频分量。为了解决这个问题，需要使用低通滤波器来滤除这些高频分量。在实际应用中这些被称为抗混叠滤波器（anti-alias filters）

当采样频率为最高频率2倍时（采样定理），原始信号才能完全被采样信号表达（无混叠问题）。

S域和Z域及其稳定性

S到Z的映射

s plane 到 z plane 的映射

在信号与系统中学过，S域用于衡量连续系统，Z域用于衡量离散系统。其中S域到Z域的推导就是令$z=e^{Ts}$，其中$s=j\omega+\sigma$。分离一下这个z:

$$z=e^{Ts}=e^{T(j\omega+\sigma)}=e^{T\sigma}e^{jT\omega}$$

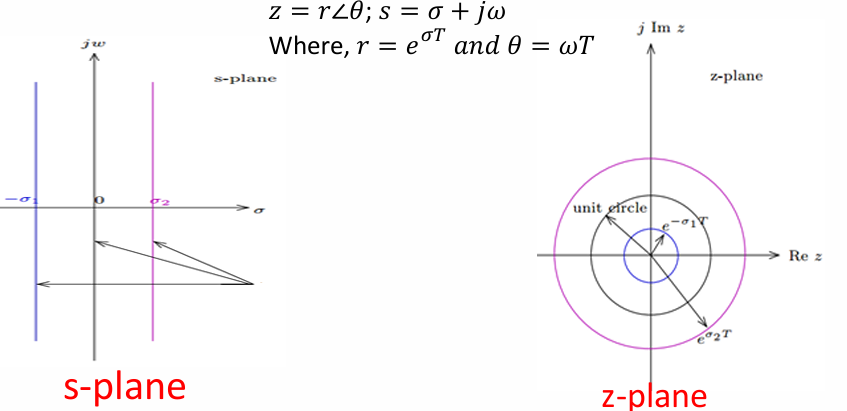
此时，这个复数z的幅值完全由$e^{T\sigma}$贡献，角度完全由$e^{jT\omega}$贡献。因此可以记为$z=r\angle\theta$，其中$r=e^{T\sigma}$，$\theta=\omega T$

回想s平面，其横轴为$\sigma$，纵轴为$\omega$。现在到了z平面，原本的横轴映射为了幅值；原本的纵轴映射成了角度。原本位于横轴n处的一条垂直的线（即，$\sigma=n,\omega不限$）现在变成了幅值为n的一个圆（即，$r=e^{Tn},\theta=\omega T=不限$）。

因此s平面到z平面的映射，就是把它s平面上的竖线卷成一个圆；其中s平面左侧的因为$\sigma<0$，因此：

• $r=e^{\sigma T}<1$，在单位圆内。
• 位于虚轴上的$\sigma=0$，对应$r=1$，位于单位圆上。
• 位于右半平面的$\sigma>0$，映射到的就是$r>1$的单位圆外。

如下图所示

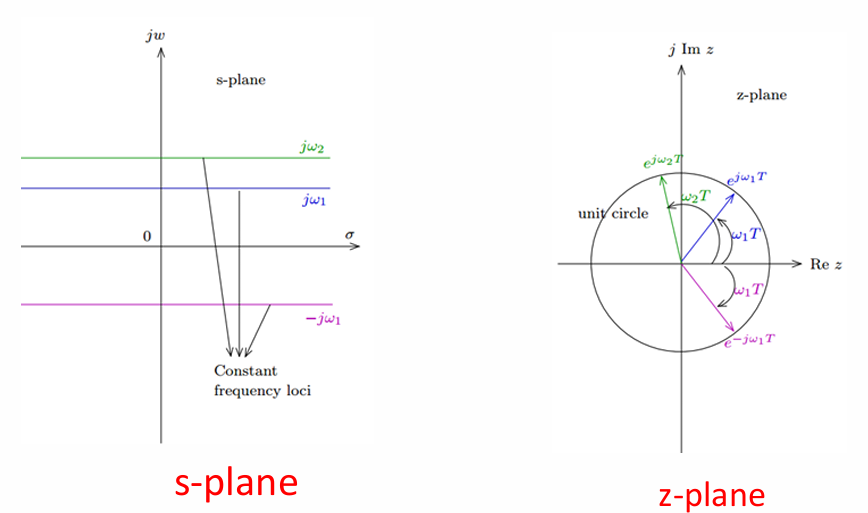
这样卷起来之后，原本在s平面水平的横线就被卷成了指向某一个方向的向量，如下图所示。从数学的角度也很好解释：某一条水平横线的表达式为$s=j\omega$，$\sigma$不限。映射到z就是$\theta=\omega T$，$r=e^{\sigma T}$不限。

终值定理和稳态误差转换

在Part1介绍的拉普拉斯变换中介绍了unit step, unit ramp, 和 acceleration input的steady state error。这里将它们映射到Z域（其实用映射不是很准确，除了终值定理遵循映射关系，它的公式其实是由z系统下表示的系统函数推导出来的）

单位阶跃响应

• 在s域下：$K_p=\lim_{s\rightarrow0}{G(s)H(s)}$，稳态误差：$e_{ss}=\frac{1}{1+K_p}$
• 在z域下：$K_p=\lim_{z\rightarrow1}{GH(z)}$，稳态误差：$e_{ss}=\frac{1}{1+K_p}$

type0系统稳态误差存在，1阶及以上不存在。注意这里的type还是由分母孤立的s来定义，并非z。

单位斜坡响应

• 在s域下：$K_V=\lim_{s\rightarrow0}{sG(s)H(s)}$，稳态误差：$e_{ss}=\frac{1}{K_V}$
• 在z域下：$K_V=\lim_{z\rightarrow1}{\frac{(1-z^{-1})GH(z)}{T}}$，稳态误差：$e_{ss}=\frac{1}{K_V}$

type0系统稳态误差为无穷，type1为$\frac{1}{K_V}$，type2及以上无稳态误差

单位加速度响应

• 在s域下：$K_a=\lim_{s\rightarrow0}{s^2G(s)H(s)}$，稳态误差：$e_{ss}=\frac{1}{K_a}$
• 在z域下：$K_a=\lim_{z\rightarrow1}{\frac{(1-z^{-1})^2GH(z)}{T^2}}$，稳态误差：$e_{ss}=\frac{1}{K_a}$

type0,1稳态误差为无穷，type2为$\frac{1}{K_a}$

s域的极点和时域响应的关系

实数根和收敛速度的关系

考虑一个系统：$G(s)=\frac{1}{s+a}$，这个系统的极点为$s=-a$，对单位冲击函数$\delta(t)$的响应就是传递函数本身，即$U(s)=\frac{1}{s+a}$，那么有：

$$u(t)=e^{-at}$$

如果a为正数，即极点在左边平面，这个响应呈现随时间衰减趋势，且a越大衰减越快；如果a为负数，即极点在右半平面，这个响应呈现随时间增加趋势，且a越小递增越快。

对应极点，就是极点越靠近负无穷，衰减越快，极点越靠近正无穷，增加越快，极点在0附近这个函数更趋于平缓

主导极点

考虑一个二阶系统$G(s)=\frac{1}{s^2+2\zeta\omega_ns+\omega_n^2}$，对其施加单位冲击响应，输出为系统函数本身。系统函数的极点可令分母等于0后使用求根公式获得：

$$P=-\zeta\omega_n\pm\omega_n\sqrt{\zeta^2-1}$$

当$\zeta>1$时：

$\sqrt{\zeta^2-1}>0$，$P_1,P_2$都为实数。输出可以写成：

$$U(s)=\frac{1}{(s-P_1)(s-P_1)}=\frac{A}{s-P_1}+\frac{B}{s-P_2}$$ $$u(t)=Ae^{P_1t}+Be^{P_2t}$$

假设两个极点都在右半平面。由于$P_1=-\zeta\omega_n+\omega_n\sqrt{\zeta^2-1}>P_2=-\zeta\omega_n-\omega_n\sqrt{\zeta^2-1}$，遵照上面将的离负无穷越近收敛越快，$P_1$这收敛较慢，$P_2$收敛较快。系统由这两部分叠加，收敛较慢的信号决定了系统的收敛速度，因此称$P_1$为主导极点。（此时也对应了严阻尼，无过冲收敛的情况）

虚部根于震荡频率的关系

继续考虑前面的二阶系统，当$\zeta$=0时

$$P_1=-\zeta\omega_n+\omega_n\sqrt{\zeta^2-1}=\omega_n\sqrt{-1}=j\omega_n$$ $$P_2=-\zeta\omega_n-\omega_n\sqrt{\zeta^2-1}=-\omega_n\sqrt{-1}=-j\omega_n$$

此时这两个根完全在虚轴上，无实部分量。系统输出为：

$$U(s)=\frac{1}{(s-j\omega_n)(s+j\omega_n)}=\frac{1}{s^2+\omega_n^2}$$ $$u(t)=\frac{1}{\omega_n}sin(\omega_nt)$$

可以看到，此时系统输出以$\omega_n$的频率进行震荡，且$|\omega_n|$越大震荡的频率越快。因此，极点在虚轴上距离零点越远，震荡频率越快（此时也对应了无阻尼，自由震荡的情况）

结合实部和虚部的关系

继续考虑前面的二阶系统，当0<$\zeta$<1时

$$P_1=-\zeta\omega_n+\omega_n\sqrt{\zeta^2-1}=-\zeta\omega _n+j\omega_n\sqrt{1-\zeta^2}$$ $$P_2=P=-\zeta\omega_n-\omega_n\sqrt{\zeta^2-1}=-\zeta\omega _n-j\omega_n\sqrt{1-\zeta^2}$$

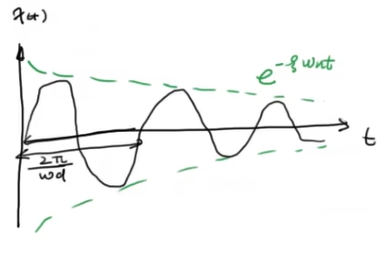
定义$\omega_d=\omega_n\sqrt{1-\zeta^2}$，称为固有频率，此时:

$$U(s)=\frac{1}{(s+\zeta\omega _n+j\omega_d)(s+\zeta\omega _n-j\omega_d)}=\frac{1}{(s+\zeta\omega_n)^2+\omega_d^2}$$ $$\frac{1}{\omega_d}\frac{\omega_d}{(s+\zeta\omega_n)^2+\omega_d^2}$$ $$u(t)=\frac{1}{\omega_d}e^{-\zeta\omega_nt}sin(\omega_dt)$$

其图像是包络为$e^{-\zeta\omega_nt}$，以$\omega_d$为频率震荡收敛的函数。因此根的虚部大小（$\omega_d$）决定了其震荡频率，实部大小（$-\zeta\omega_n$）决定了其收敛速度。（对应欠阻尼情况）。

总结和映射至Z平面

总结一下，在s域内：

• 极点虚部绝对值越大信号的震荡频率越快
• 极点实部在左半平面，信号收敛；越靠近负无穷收敛越快
• 极点实部在右半平面，信号发散；约靠近正无穷发散越快
• 极点无实部只有虚部时，为临界稳定状态，保持固有频率震荡

考虑s平面和z平面的映射关系，在z域内：

• 极点相位角越大震荡频率越快
• 极点模长小于1时，信号收敛；越靠近0收敛越快
• 极点模长大于1时，信号发散；越靠近无穷发散越快
• 极点模长等于1时，为临界稳定状态，保持固有频率震荡

最终可以得到下图：

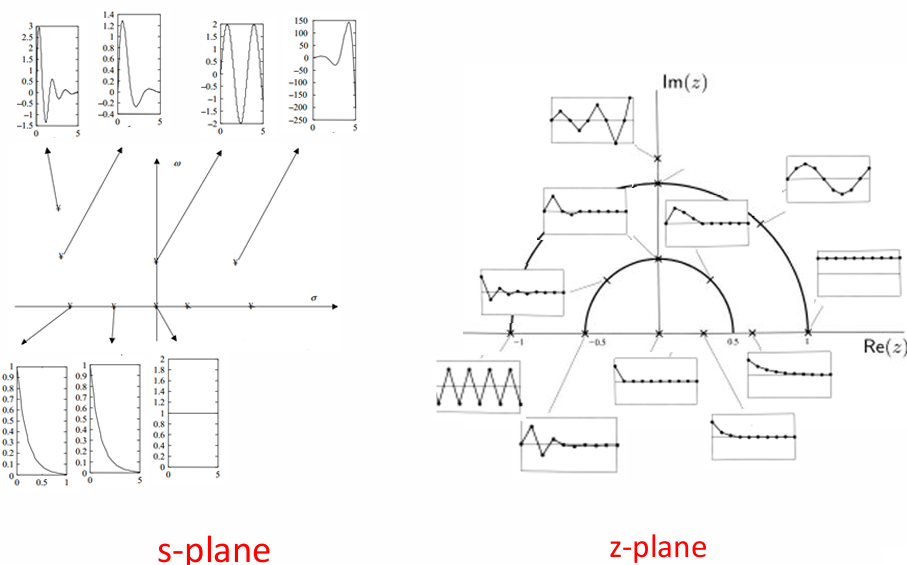
s域和z域稳定性关系

在上一节的分析中可以得出：

• s域所有极点在左半平面系统稳定；z域所有极点在单位圆内系统稳定
• s域有极点在虚轴上系统临界稳定；z域所有极点在单位圆上系统临界稳定
• s域所有极点在右半平面系统不稳定；z域所有极点在单位圆外系统不稳定

Z域下的稳定性判据

同前面介绍Routh-Hurwitz稳定性判据时一样，对于低阶系统，我们可以轻易得求得其零极点。但是对于高阶系统这比较困难。因此需要稳定性判据。前面介绍过的s域下的Routh-Hurwitz稳定性判据，这里会介绍 Jury’s Stability test 和 Bilinear transformation 映射到z域下的Routh-Hurwitz稳定性判据

Jury’s Stability test

类似于 Routh - Hurwitz 方法，Jury’s Stability test 也是一个基于数理的稳定性测试。它用于确定多项式的根是否位于单位圆内。

考虑以下形式的传输函数特征方程：（$a_0>0$）

$$F(z)=a_0z^n+a_1z^{n-1}+...a_{n-1}z+a_n=0$$

与Routh-Hurwitz稳定性判据类似，Jury’s Stability test 也有一张表，需要使用的行数由特征方程的最高阶决定：$行数=2n-3$。例如假设最高是$z^4$，则需要5行。

• 表中第一行以逆序和顺序的方式写上系统特征方程的系数。

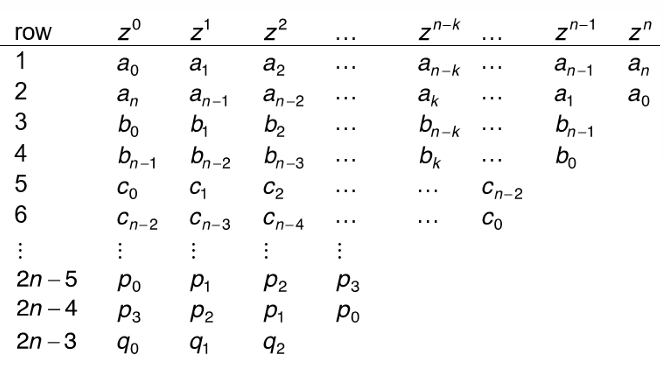
• $b_k,c_k$的计算方法为：

$$b_k= \left|\begin{array}{cc} a_0 & a_{n-k}\\ a_n & a_{k}\\ \end{array}\right|=(a_0\times a_{k}-a_n\times a_{n-k})$$ $$c_k= \left|\begin{array}{cc} b_{0} & b_{n-1-k}\\ b_{n-1} & b_{k}\\ \end{array}\right|=(b_{0}\times b_{k}-b_{n-1}\times b_{n-1-k})$$

如下面三图所示

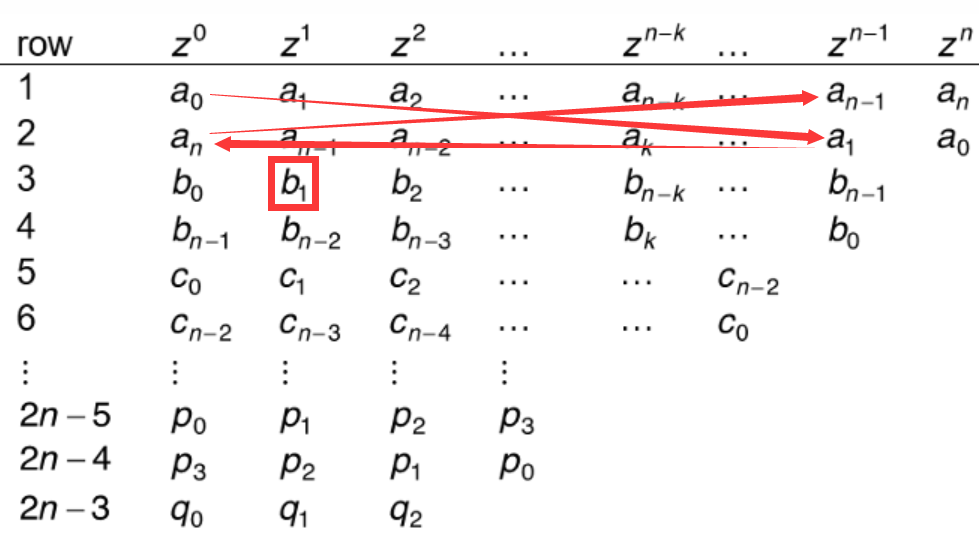
如果满足以下条件则系统稳定

1. $F(1)>0$
2. $(-1)^nF(-1)>0$
3. $|a_0|<a_n$
4. $|b_0|>|b_{n-1}|,|c_0|>|c_{n-2}|…$直到最后一个

举个例子：$F(z)=z^4-1.2Z^3+0.07z^2+0.3z-0.08$

step1 先对$F(1)$和$(-1)^nF(-1)>0$进行判断：

$$F(1)=1^4-1.21\times1^3+0.07\times1^2+0.3\times1-0.08=0.09>0$$ $$(-1)^nF(-1)=(-1)^4[(-1)^4-1.21\times(-1)^3+0.07\times(-1)^2+0.3\times(-1)-0.08]=1.89>0$$

step2 再对$|a_0|<a_n$进行判断：

$$|a_0|=0.08<1$$

step3 最后再计算表格，对$|b_0|>|b_{n-1}|,|c_0|>|c_{n-2}|…$进行判断。Z有4阶，因此需要$2\times4-3=5$，因此使用5行。

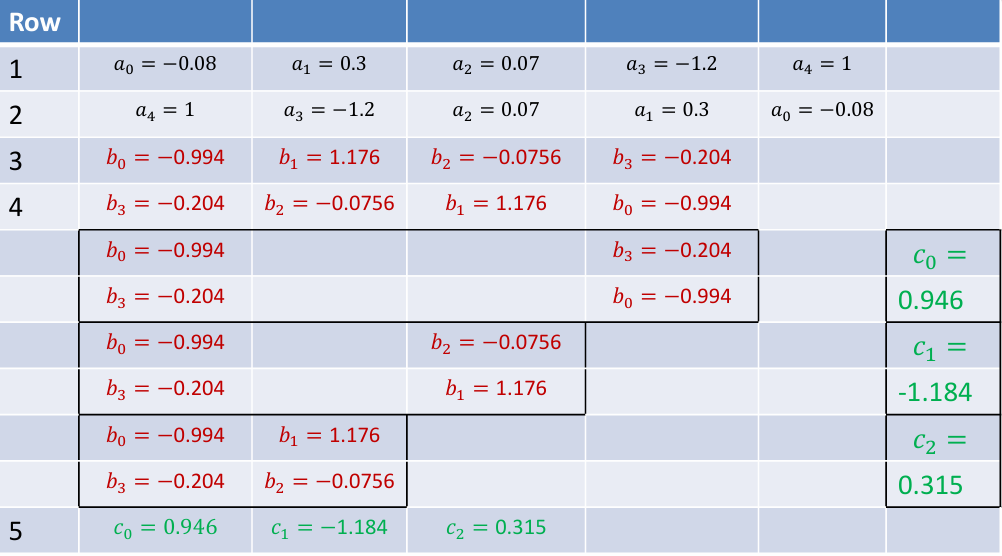
最后发现

$$|b_0|>|b_3|,|c_0|>|c_2|$$

因此系统稳定。

bilinear transformation coupled with the Routh stability criterion

Part1的Routh stability criterion只适用于s域，但是现在需要讨论离散的z域。这里的方法是使用 bilinear transformation 将z域映射回s域（它这里记作$w$域）：

$$z=\frac{w+1}{w-1},w=\sigma+j\omega$$

映射回去之后，对$w$套用Routh-Hurwitz准则

举个例子：

采样后的数字控制系统

简单回顾：Z变换

抽头形式

在时域的一个信号，经过脉冲抽样器采样之后会变成下图右侧的样子。其数学表示为

$$x^*(t)=\sum_{k=0}^{\infty}x(kT)\delta(t-kT)=x(0)\delta(t)+x(T)\delta(t-T)+...+x(kT)\delta(t-kT)...$$

这个式子的z变换为：

$$X(z)=\sum_{k=0}^{\infty}x(kT)z^{-k}=x(0)z^0+z(T)z^{-1}+...+x(kT)z^{-k}+...$$

其中$T$为采样周期，$z^{-k}$就是延迟器（Recall：数字信号处理）

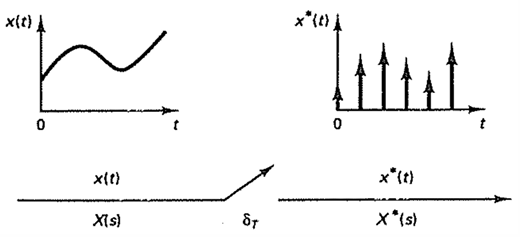
S变换-时域-Z变换间的关系

以时域作为媒介，可以使用上述变化对直接对s域到z域进行变换。

引入-冲击采样的传输系统

引入-采样输入，采样输出

考虑这样的一个系统：

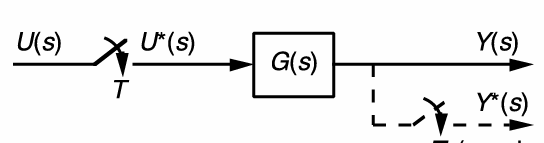
在模拟情况下：

$$Y(s)=U(s)G(s)$$

如果将$U(s)$采样为$U^*(s)$，则是：

$$Y(s)=G(s)U^*(s)$$

如果对输出的$Y(s)$也进行采样为$Y^*(s)$，则可以看成两个离散序列卷积，是：

$$Y^*(s)=(G(s)U^*(s))^*=G^*(s)U^*(s)$$

相当于对模拟系统离散化后，再和离散化的信号卷积。模拟信号离散化可以表示为z变换：

$$G(z)=\sum_{k=0}^{\infty}g(kT)z^{-k}$$

其中$g(kT)$是对模拟信号的单位冲击响应的采样序列。因此：

$$Y(z)=G(z)U(z)$$

采样输入，采样传递，采样输出

再考虑这样一个系统：

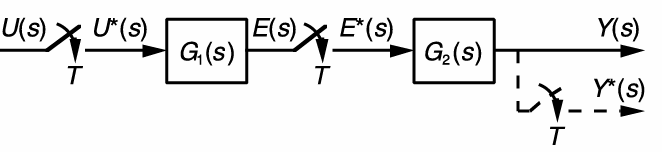
根据引入里面的结论，这个系统的表达式可以写为：

$$Y(z)=G_1(z)G_2(z)U(z)$$

传递函数为：

$$\frac{Y(z)}{U(z)}=G_1(z)G_2(z)$$

采样输入，模拟传递，采样输出

那么对于这个系统：

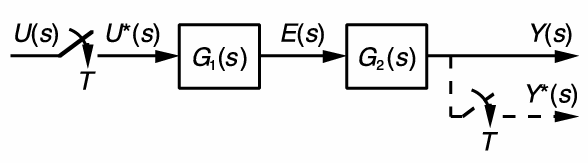
首先对$U(s)$进行采样，输入系统$G_1(s)$，有：

$$E(s)=U^*(s)G_1(s)$$

$E(s)$会以模拟信号的形式输入$G_2(s)$，有：

$$Y(s)=E(s)G_2(s)=U^*(s)G_1(s)G_2(s)$$

对$Y(s)$进行采样，有：

$$Y^*(s)=(G_1(s)G_2(s)U^*(s))^*=(G_1(s)G_2(s))^*U^*(s)$$

因此传递函数为

$$\frac{Y(z)}{U(z)}=G_1G_2(z)$$

注意！$G_1G_2(z)\neq G_1(z)G_2(z)$

使用0阶保持器（Zero-Order Hold，ZOH）将数字信号输入模拟系统

ZOH的系统函数

ZOH可以将离散的数字信号保持一段时间，使其可以输入模拟系统。如下图所示

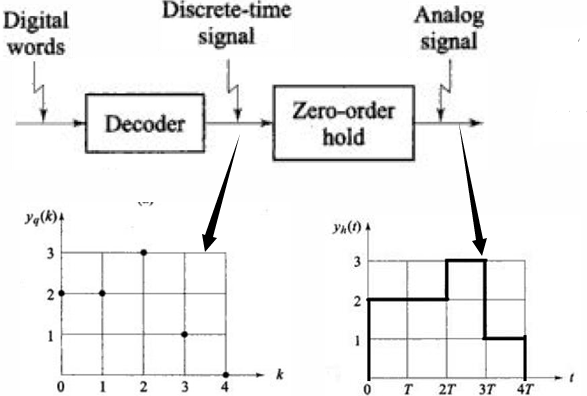
假设ZOH的保持时间为T，那么其对单位冲激函数的输入会保持T的时间，可以写成时移的两个u(t)相减：

$$ZOH(t)=1(t)-1(t-T)$$ $$ZOH(s)=\frac{1}{s}-\frac{e^{-Ts}}{s}=\frac{1-e^{-Ts}}{s}$$

因为单位冲激函数的响应恰好就是系统函数，因此ZOH的函数就是：

$$ZOH(s)=\frac{1-e^{-Ts}}{s}$$

将ZOH输入模拟系统

将ZOH进入模拟系统$G(s)$后的输出记为$G_{ZA}(s)$

$$G_{ZA}(s)=\frac{1-e^{-Ts}}{s}G(s)=(1-e^{-Ts})\frac{G(s)}{s}=\frac{G(s)}{s}-e^{-Ts}\frac{G(s)}{s}$$

如果将$G_{ZA}(s)$的输出离散采样，回顾一下，时域时移性质在Z变换下和S变换下的表达式：

$$L[f(t-t_0)]=F(s)e^{-st_0}$$ $$Z[f(t-kT)]=z^{-kT}F(z)$$

因此我们可以得到：$Z[f(s)e^{-kTs}]=z^{-k}Z[F(s)]]$。所以上式可以写为：

$$G_{ZA}(Z)=Z[\frac{G(s)}{s}]-z^{-1}Z[\frac{G(s)}{s}]=(1-z^{-1})Z[\frac{G(s)}{s}]$$ $$=\frac{z-1}{z}Z[\frac{G(s)}{s}]$$

至此我们得到了ZOH输入模拟系统，再对输出采样的结果。这里的$Z[\frac{G(s)}{s}]$需参照上面S变换-时域-Z变换间的关系的表格，直接使用s变换对映射到z变换对来进行变换。

总结一下：

$$ZOH(s)=\frac{1-e^{-Ts}}{s}$$ $$G_{ZA}(s)=\frac{G(s)}{s}-e^{-Ts}\frac{G(s)}{s}$$ $$G_{ZA}(z)=\frac{z-1}{z}Z[\frac{G(s)}{s}]$$

采样周期与系统稳定性的关系

考虑如下这个系统

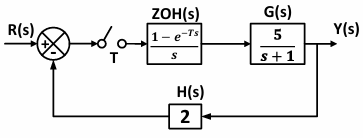
系统传递函数为$G_{ZA}(z)$，根据上面总结的公式：

$$G_{ZA}(z)=\frac{z-1}{z}Z[\frac{G(s)}{s}]=(\frac{z-1}{z})Z[\frac{5}{s(s+1)}]$$

由变换对$\frac{1}{s(s+a)}=\frac{1}{a}(1-e^{-at})=\frac{z(1-e^{-aT})}{a(z-1)(z-e^{-aT})}$可以算得：

$$G_{ZA}(z)=5(\frac{z-1}{z})(\frac{z(1-e^{-t})}{(z-1)(z-e^{-t})})$$ $$=5\frac{1-e^{-T}}{z-e^{-T}}$$

其中T为采样周期

系统的$OLTF(s)=H(s)ZOH(s)G(s)$，$OLTF(z)=2G_{ZA}(z)$，因此：

$$OLTF(z)=10\frac{1-e^{-T}}{z-e^{-T}}$$

系统的$CLTF(z)=\frac{G_{ZA(z)}}{1+OLTF(z)}$

$$CLTF(z)=\frac{5\frac{1-e^{-T}}{z-e^{-T}}}{1+10\frac{1-e^{-T}}{z-e^{-T}}}=\frac{5(1-e^{-T})}{z-11e^{-T}+10}$$

系统特征方程为：$z-11e^{-T}+10=0$，系统极点为$z=11e^{-T}-10$。对于z域，要求所有极点模长小于1，系统稳定，即：

$$11e^{-T}-10<1 \&11e^{-T}-10>-1$$ $$e^{-T}<1, -T<ln(1)=0,T>0$$ $$e^{-T}>9,-T<ln(\frac{9}{11}), T<0.2$$

因此，求得若要系统稳定，采样周期必须$0<T<0.2$。那么最小采样频率（称为critical frequency）必须大于$f_{critical-frequency}=\frac{1}{T_{max}}=5Hz$，采样频率等于最小采样频率时，系统临界稳定。