电信传输理论-CH6-光传输线
引入
对于光而言,其频率非常高,因此在讨论光时一般不直接讨论频率,而转为讨论光波的波长(通常以nm为单位)。
最开始的时候,塑料光纤作为“打通光纤通信最后一米,让用户终端使用光通信”的存在,有很多人在研究。这种光纤只能在较短距离内传输。但是它最终还是没有赶上时代,现在使用较少。
在CH3中简略介绍过光纤,其中介绍了单模和多模光纤,其粗细有差异。一般来说,单模线芯粗细约为9um,多模线芯粗细越为50um。
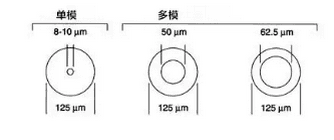
将光纤无法做“接头”,因为光的指向性非常明确。一能一条线做一个“插头”。同时,光纤间连接时需要使用融纤机进行融接。
在光纤传输系统中,首先使用发光二极管(light-emitting diodes)将电信号转化为光,在接收端再用光电二极管(photodiodes)转化为电信号。
没有发射设备发出单一频率的辐射。LED 的输出线宽(linewidth)通常约为 60 nm,激光器的线宽为 5 至 10 nm,而“单模激光器”的线宽可以小于 0.01 nm。这与本节中会介绍的色散有关,这代表即使信号源是单色的(单频),也会发生频率扩展。
光纤的通信能力有如下参数来量化:
- 光接接收度(light acceptance)
- 光损耗(light loss)
- 带宽(Bandwidth)
这三个参数由两个更底层的物理性质决定:光纤的有效直径(active diameter)和光纤内使用的材料的折射率(refractive)。下面将介绍由数学量化的光纤分析:
光的折射和反射理论
折射率(Refractive Index)
光纤的折射率用n来表达,其定义如下
(由定义式可以看出,真空中折射率为1)
在光纤中,其介质不同程度地会阻碍光,因此光速比真空中慢。折射率>1
同时,不同的波长在同一介质中传输速率也有差异,因此波长不同,在同一介质下折射率也不同。因此,光的折射率需要针对某个波长来讨论:
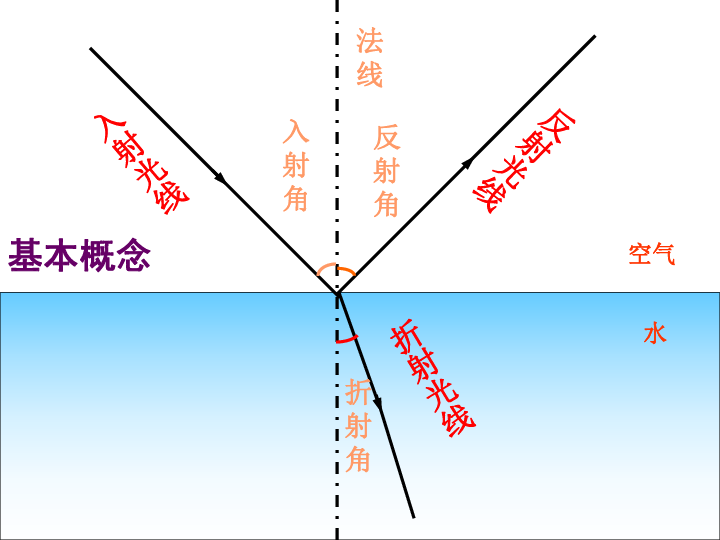
光通信中常用波长如下图所示,这里五星级的是CH3中介绍的850nm,1310nm,1550nm三个传输窗口。
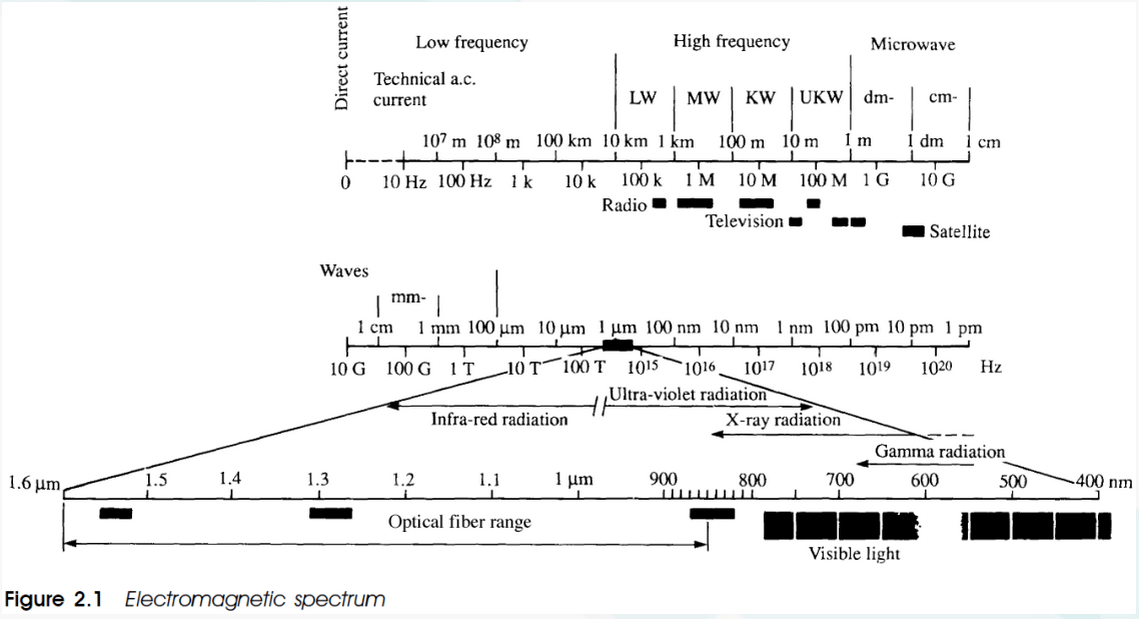
反射和折射的基本理论
这里五星级!
折射
对于两个具有不同折射率$n_1,n_2$的介质,光的折射遵循如下规则:
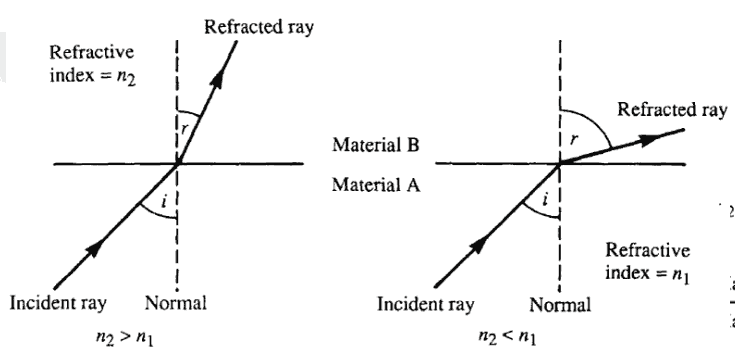
其中,入射角$i$和出射角$r$关系如下:
或者可以把入射和反射都放在等号两边便于记忆:
可以看到,当$n_2<n_1$时,出射角会大于入射角。假如增大入射角,则出射角也会一起增大,如下图箭头所示方向
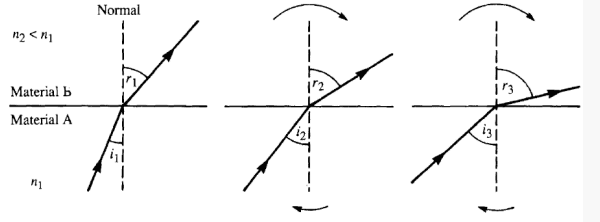
则出射角可能大于90度。这就会产生“全反射”
反射
当光经过界面时,一部分会被折射,一部分会被反射。对于反射而言,入射角等于反射角。
全反射(total internal reflection)
对于不同折射率的介质,当光线从光密介质(较高折射率的介质)进入到光疏介质(较低折射率的介质),入射角大于临界角(critical angle)时,会发生全反射(total internal reflection):光线全部向内面反射(没有能量损耗),同时入射角等于出射角。对应下图就是$n_1>n_2$
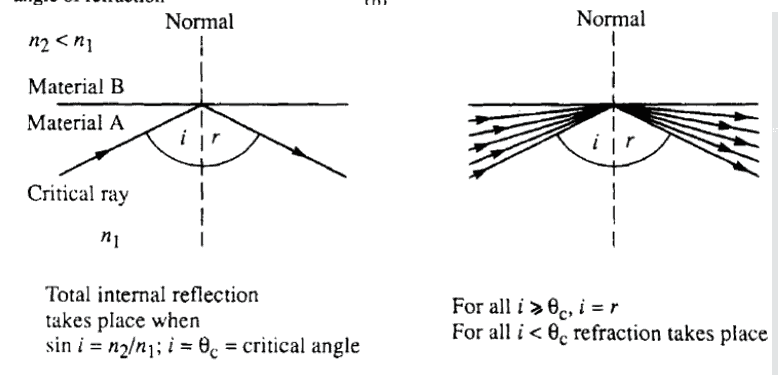
其中,临界角(critical angle)的计算公式是:
由上可以看出,光纤中,线芯的折射率高于包层
非涅尔反射(Fresnel reflection)
当光从一种折射率为$n_1$的介质向另一种折射率为$n_2$的介质传播时,在两者的交界处(通常称作界面)若入射角小于临界角度,则会同时发生光的反射和折射。如下图
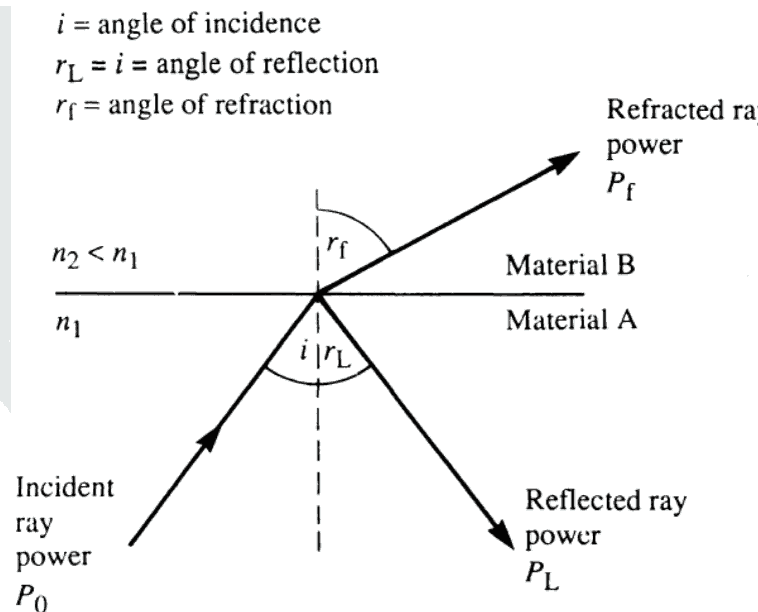
这样不全的反射就被称为非涅尔反射。其中入射功率$P_0$,折射功率$P_f$,反射功率$P_L$关系如下:
光纤传输理论
光纤内部的全内反射(介绍)
引入
在 18 世纪,人们发现光可以通过液体射流来引导,因为液体内具有高折射率,当液体穿过周围的低折射率空气时,液体内的光将会发生全反射

这个过程使用反射方程来建模,即可得到下图。因此,理论来说,使用一个纤芯,只要入射角满足临界角条件即可对光实现引导。
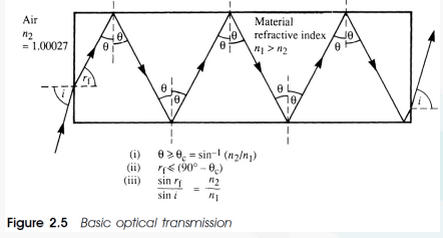
但是上图是非常理想的core,实际制造中,core的表面其实是凹凸不平的,因此会造成一部分损耗。称之为“Surface defects”,如下图所示
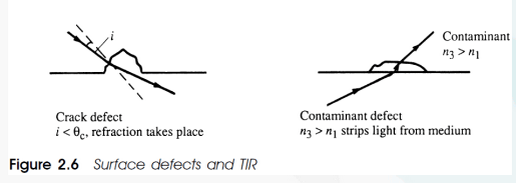
因此,仅仅和使用纤芯来对光进行引导是不够的,需要在纤芯外面再加一层包层,包层折射率小于纤芯 (实际应用中通常$n_1$和$n_2$差值很小)。
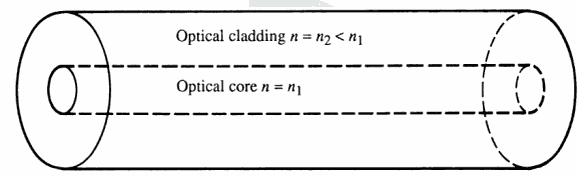
这样的结构被称为core–cladding interface (CCI)。通常根据纤芯径和包层直径来定义光纤,以微米为单位。下图是一些常见的光纤参数(不需要记)

阶跃光纤内的两种传输方式
当一東光线从光纤端面耦合进光纤时,光纤中有两种传输的方式:
- 一种是光线始终在一个包含光纤中心轴的平面内传播,并且一个传播周期与中心轴相交两次,这种光线常称为子
午线,包含光纤中心轴的固定平面就称为子午面,如下图(a)中MN平面所示; - 另一种其传播的轨迹不在同一个平面内,并不与光纤中心轴相交,这种光线就称为斜射光线,如下图(b)所示。
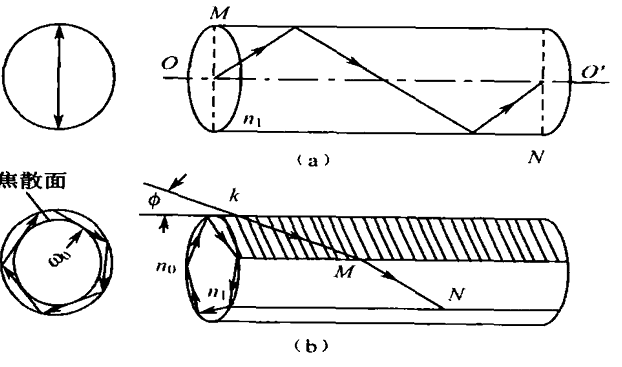
子午线阶跃光纤传播模型(五星级)
五星级例题,《电信传输原理 第2版》P90
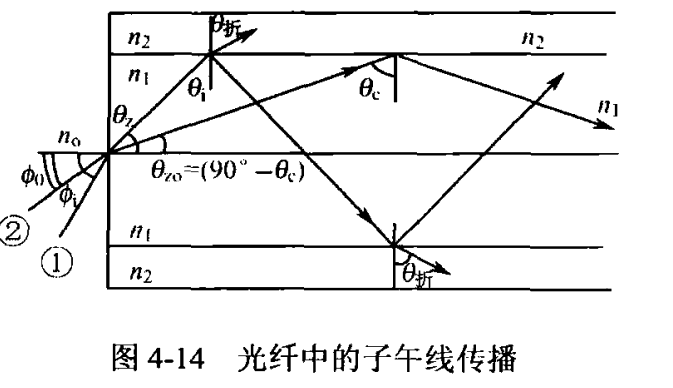
已知纤芯半径为a,折射率为$n_1$;包层折射率为$n_2$,并且$n_1>n_2$。空气的折射率为$n_0=1$
因为$n_1>n_2$,因此折射角大于入射角,可以发生全反射。
光线以$\phi_i$的角度,从空气$n_0$入射至$n_1$,因此有:(注意,这个地方的入射角和出射角和前面介绍的是情况互补的,但是公式依旧适用(可以用光路可逆来解释))
如果$\theta_i<\theta_c$,则是上图①的情况,有部分光折射出去。若$\theta_i>\theta_c$,则是②的情况,发生全反射。那么这个临界角度反应到$\phi_i$上是多少呢?记临界情况$\phi_i=\phi_0,\theta_z=\theta_{z_0},\theta_i=\theta_c$
也就是说,只要求得$n_1cos(\theta_c)$的值,就可以逆推$\phi_0$
根据折射公式$n_1sin(\theta_c)=n_2$,因此有:
如果将包层和纤芯的折射率的差异使用 相对折射率差$\Delta$来描述:
上式可以写为:
回到最初的$n_0sin(\phi_0)=n_1cos(\theta_c)$:
光纤数值孔径(Numerical Aperture, NA)
不妨直接将子午线模型中的$n_0sin(\phi_0)=n_1cos(\theta_c)$直接定义为$n_0sin(\phi_0)=NA$。其中NA为光纤数值孔径,表征光纤收集光的能力。
可见,纤芯与包层折射率差异$\Delta$越大,NA越大,代表光线集光能力越强。通信用的光纤NA较小,故称为弱导光纤。
如果遇到光的接受度(light acceptance),就是NA
光纤的传输损耗
光纤的损耗可以大体分为:
- 光纤本身的传输损耗:由光纤本身物理性质产生的损耗。
- 光纤使用事引起的传输损耗:在安装时,由于弯曲/接头连接/融接等操作中引起的损耗。
五星级
其中又可以分为数个小类,如下表所示。下表中前3列(就是不含最后的详细描述)要求掌握。


bnh的补充小课堂:微弯曲损耗有可能是在从光纤生产到光缆的过程中产生的。由于生产工艺造成了一些应力不均等,造成了光纤产生了非常非常微小的弯曲。
色散特性
多模模式色散(mode dispersion)
模式色散一般存在于多模光纤中。因为,在多模光纤中同时存在多个模式,不同模式沿光纤轴向传播的群速度不同,它们到达终端时,必定会有先有后,出现时延差,形成模式色散,从而引起脉冲宽度展宽,如下图所示。
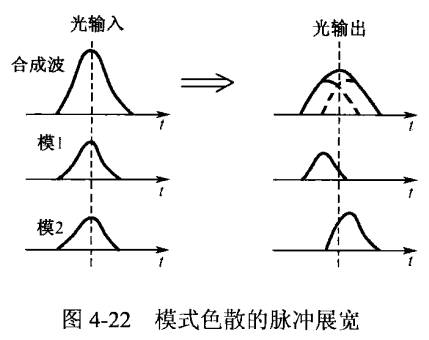
材料色散(materialdispersion)
光波在光学介质中传播时其介质材料的折射率n随波长λ变化而产生的,使得各波长的光信号传播速度不同,在接收端产生的波形时域扩展的现象。
波导色散(waveguide dispersion)
波导色散是对于光纤的某一传输模式,在不同的光波长下的群速度不同引起的脉冲展宽。它与光纤结构的波导效应有关,因此也被成为结构色散。
偏振色散(Polarization Mode Dispersion)
一个信号脉冲沿着理想的对称圆形单模光纤在不受外界干扰情况下传输时,光纤输入端的光脉冲可分裂成两个垂直的偏振输出脉冲,以相同的的传播速度进行传输,并同时到达光纤输出端,这两个脉冲叠加在一起会重现出它们在光纤输入端时的偏振状态,实际上光纤由于上文所述的种种原因,会引起双折射,即x轴方向和y轴方向上的折射率是不一样的,这将引起偏振模色散(Polarization Mode Dispersion)
- 多模光纤:模式色散为主
- 单模光纤:材料色散为主